山东省济南市历下区2020-2021学年八级上学期数学期中试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 已知一个数的立方根是﹣ ,那么这个数是( )A、﹣ B、 C、 D、﹣2. 下列数是无理数的是( )A、﹣ B、π C、0 D、0.23. 下列函数中,y是x的正比例函数的是( )A、y=6x-1 B、y= C、y=x2 D、y=- x4. 如图是北京市地图简图的一部分,图中“故宫”、“颐和园”所在的区域分别是( )
D
E
F
6
颐和园
奥运村
7
故宫
日坛
8
天坛
A、D7,E6 B、D6,E7 C、E7,D6 D、E6,D75. 下列选项中,运算正确的是( )A、3 =3 B、 =7 C、 =5 D、 =126. 在平面直角坐标系中,点P(-2,x2+1)所在的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 在平面直角坐标系中,若点 与点 之间的距离是5,那么y的值是( )A、-2 B、8 C、2或8 D、-2或88. 已知点A(﹣2,y1),B(3,y2)在函数y=﹣3x+2的图象上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定9. 由方程组 可得x与y的关系式是( )A、3x=7+3m B、5x﹣2y=10 C、﹣3x+6y=2 D、3x﹣6y=210. 已知正比例函数y=kx的图象如图所示,则一次函数y=kx﹣k的图象是( ) A、
A、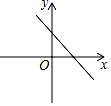 B、
B、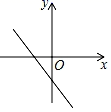 C、
C、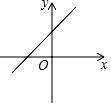 D、
D、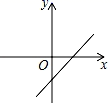 11. 某运输队接到给武汉运输物资的任务,该队有 型卡车和 型卡车, 型卡车每次可运输 物资,每天可运输5次, 型卡车每次可运输 物资,每天可运输4次,若每天派出20辆卡车,刚好运输 物资,设该运输队每天派出 型卡车 辆, 型卡车 辆,则所列方程组正确的是( )A、 B、 C、 D、12. 如图,直线y=kx(k≠0)与y= x+2在第二象限交于A,y= x+2交x轴,y轴分别于B、C两点.3S△ABO=S△BOC , 则方程组 的解为( )
11. 某运输队接到给武汉运输物资的任务,该队有 型卡车和 型卡车, 型卡车每次可运输 物资,每天可运输5次, 型卡车每次可运输 物资,每天可运输4次,若每天派出20辆卡车,刚好运输 物资,设该运输队每天派出 型卡车 辆, 型卡车 辆,则所列方程组正确的是( )A、 B、 C、 D、12. 如图,直线y=kx(k≠0)与y= x+2在第二象限交于A,y= x+2交x轴,y轴分别于B、C两点.3S△ABO=S△BOC , 则方程组 的解为( )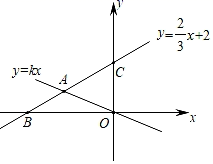 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
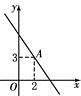
13. 4的算术平方根是 .14. 若(x﹣y+3)2+ =0,则x+y的值为 .15. 若将直线 的图象向上平移 个单位后经过点 ,则平移后直线的解析式 .16. 已知直线y=x+b和y=ax﹣3交于点P(2,1),则关于x的方程x+b=ax﹣3的解为 .17. 如图,一次函数 ( )的图象经过点A.当 时,x的取值范围是 .
 18. 如图,在一单位为1的方格纸上, ,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若 的顶点坐标分别为 ,则依图中所示规律, 的坐标为 .
18. 如图,在一单位为1的方格纸上, ,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若 的顶点坐标分别为 ,则依图中所示规律, 的坐标为 .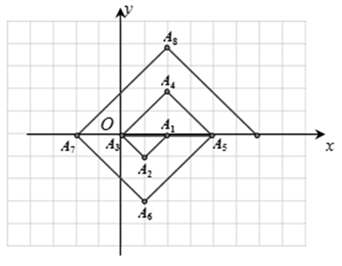
三、解答题
-
19. 计算:(1)、 ;(2)、 ﹣ .20. 用指定的方法解下列方程组:(1)、 (代入法);(2)、 (加减法).21. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,7),(﹣1,5).
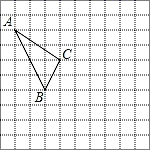
⑴请在如图所示的网格平面内画出平面直角坐标系;
⑵请画出△ABC关于y轴对称的△A1B1C1;
⑶直接写出点B1的坐标.
22.(1)、利用平方根的意义,求满足条件的x值:(x﹣1)2=36;(2)、已知a=2 ﹣ ,b=2 ,求a2﹣ab的值.23. 已知直线l1:y=kx+b经过点A( ,2)和点B(2,5).(1)、求直线l1的表达式;(2)、求直线l1与坐标轴的交点坐标.24. 历下区某中学积极响应国家号召,落实垃圾“分类回收,科学处理“的政策,准备购买A、B两种型号的垃圾分类回收箱共20只,放在校园各个合适位置,以方便师生进行垃圾分类投放.学校共支付费用4240元,A、B型号价格信息如表:型号
价格
A型
200元/只
B型
240元/只
(1)、请问学校购买A型和B型垃圾回收箱各是多少只?(2)、若学校都购买A型垃圾回收箱,能节省费用多少元?25. [阅读材料]把分母中的根号化去,使分母转化为有理数的过过程,叫做分母有理化.通常把分子、分母同时乘以同一个不等于0的数,以达到化去分母中根号的目的.
例如:化简 .
解: = = ﹣ .
[理解应用]
(1)、化简: ;(2)、若a是 的小数部分,化简 ;(3)、化简: + +…+ .26. 我市全民健身中心面向学生推出假期游泳优惠活动,活动方案如下.方案一:购买一张学生卡,每次游泳费用按六折优惠;
方案二:不购买学生卡,每次游泳费用按八折优惠.
设某学生假期游泳x(次),按照方案一所需费用为 (元),且 ;按照方案二所需费用为 (元),且 .其函数图象如图所示.
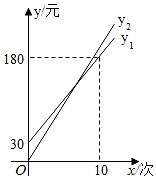 (1)、求y1关于x的函数关系式,并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用;(2)、求打折前的每次游泳费用和k2的值;(3)、八年级学生小明计划假期前往全民健身中心游泳8次,应选择哪种方案所需费用更少?说明理由.27. 如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)、求y1关于x的函数关系式,并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用;(2)、求打折前的每次游泳费用和k2的值;(3)、八年级学生小明计划假期前往全民健身中心游泳8次,应选择哪种方案所需费用更少?说明理由.27. 如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).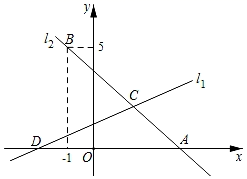 (1)、求k、b和m的值;(2)、求△ADC的面积;(3)、在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;(4)、若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,清说明理由.
(1)、求k、b和m的值;(2)、求△ADC的面积;(3)、在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;(4)、若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,清说明理由.