山东省济南市历城区2020-2021学年八级上学期数学期中试卷

试卷更新日期：2021-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $\frac{a + 1}{2 a - 1}$ 有意义，则a的取值范围是（）

A、a＝﹣1 B、a≠﹣1 C、a＝ $\frac{1}{2}$ D、a≠ $\frac{1}{2}$

查看试题解析
2. 下列分式约分正确的是（）

A、 $\frac{a + b}{c + d} = a c$ B、 $\frac{3 x}{12 x^{2}} = \frac{3}{12 x}$ C、 $\frac{3 a + b}{b^{2}} = 3 a b$ D、 $\frac{a^{2} b - a b^{2}}{a - b} = a b$

查看试题解析
3. 在一次数学测试中，小明成绩72分，超过班级半数同学的成绩，分折得出这个结论所用的统计量是（）

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
4. 把a³﹣9a因式分解，结果正确的是（）

A、a（a²﹣9） B、a（a+3）（a﹣3） C、（a+3）（a﹣3） D、a（a﹣9）（a+9）

查看试题解析
5. 冉冉的妈妈在网上销售装饰品．最近一周，每天销售某种装饰品的个数为：.11，10，11，13，11，13，15关于这组数据，冉冉得出如下结果，其中错误的是（）

A、众数是11 B、平均数是12 C、方差是 $\frac{18}{7}$ D、中位数是13

查看试题解析
6. 八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时，则所列方程正确的是（）

A、 $\frac{10}{x}$ - $\frac{10}{2 x}$ =20 B、 $\frac{10}{2 x}$ - $\frac{10}{x}$ =20 C、 $\frac{10}{x}$ - $\frac{10}{2 x}$ = $\frac{1}{3}$ D、 $\frac{10}{2 x} -$ $\frac{10}{x}$ = $\frac{1}{3}$

查看试题解析
7. 下图是甲、乙两同学五次数学测试成绩的折线图，比较甲、乙的成绩，下列说法正确的是（）

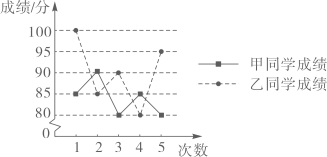A、甲平均分高，成绩稳定 B、甲平均分高，成绩不稳定 C、乙平均分高，成绩稳定 D、乙平均分高，成绩不稳定

查看试题解析
8. 对于非零实数 $a 、 b$ ，规定 $a \oplus b = \frac{1}{b} - \frac{1}{a}$ ，若 $2 \oplus (2 x - 1) = 1$ ，则 $x$ 的值为（）

A、 $\frac{5}{6}$ B、 $\frac{5}{4}$ C、 $\frac{3}{2}$ D、 $- \frac{1}{6}$

查看试题解析
9. 若关于x的分式方程 $\frac{m - 1}{x - 1}$ =2的解为非负数，则m的取值范围是（）

A、m＞﹣1 B、m≥1 C、m＞﹣1且m≠1 D、m≥﹣1且m≠1

查看试题解析
10. 已知a为整数，且 $\frac{a + 3}{a - 5} - \frac{a - 5}{a + 2}$ ÷ $\frac{a^{2} - 10 a + 25}{a^{2} - 4}$ 为正整数，求所有符合条件的a的值的和（）

A、8 B、12 C、16 D、10

查看试题解析

二、填空题

11. 某班为了解同学们一周在校参加体育锻炼的时间，随机调查了10名同学，得到如下数据：

锻炼时闭（小时）

5

6

7

8

人数

1

4

3

2

则这10名同学一周在校参加体育锻炼时间的平均数是小时．

查看试题解析
12. 若25x²+kxy+4y²是一个完全平方式，则k= ．

查看试题解析
13. 若关于x的方程 $\frac{1}{x - 2}$ +3＝ $\frac{a x - 1}{x - 2}$ 有增根，则a＝．

查看试题解析
14. 分解因式：（a﹣b）²﹣4b²= ．

查看试题解析
15. 观察下列等式：
16﹣1＝3×5；25﹣4＝3×7；36﹣9＝3×9；49﹣16＝3×11；…用自然数n（n≥1）表示上面一系列等式所反映的规律是．

查看试题解析

三、解答题

16. 因式分解：

(1)、4x²y﹣4xy²+y³ ．

(2)、a²（x﹣y）+b²（y﹣x）．

查看试题解析
17. 先化简，再选一个合适的数代入求值：（x+1﹣ $\frac{7 x - 9}{x}$ ）÷ $\frac{x^{2} - 9}{x}$ ．

查看试题解析
18. 解分式方程：

(1)、 $\frac{3}{2 x} = \frac{2}{x + 1}$ ；

(2)、 $\frac{y - 2}{y - 3} = 2 - \frac{1}{3 - y}$ ．

查看试题解析
19. 2020年2月，贵州省积极响应国家“停课不停学”的号召，推出了“空中黔课”.为了解某中学初三学生每天听空中黔课的时间，随机调查了该校部分初三学生.根据调查结果，绘制出了如下统计图表（不完整），请根据相关信息，解答下列问题：
部分初三学生每天听空中黔课时间的人数统计表

时间/ $h$

1.5

2

2.5

3

3.5

4

人数/人

2

6

6

10

$m$

4

部分初三学生每天听空中黔课时间的人数统计图

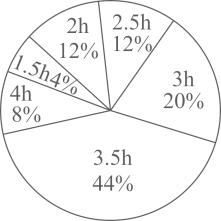(1)、本次共调查的学生人数为，在表格中， $m =$ ；

(2)、统计的这组数据中，每天听空中黔课时间的中位数是，众数是；

(3)、请就疫情期间如何学习的问题写出一条你的看法.

查看试题解析
20. 某中学为创建书香校园，去年进一批图书，经了解，科普书的单价比文学书的单价多4元，1500元购进的科普书与1000元购进的文学书本数相等，求去年购进的文学书和科普书的单价分别多少元？

查看试题解析

21. 每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心疾首．今年某校为确保学生安全，开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛．现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A.80≤x＜85，B.85≤x＜90，C.90≤x＜95，D.95≤x≤100），下面给出了部分信息：七年级10名学生的竞赛成绩是：99，80，99，86，99，96，90，100，89，82；八年级10名学生的竞赛成绩在C组中的数据是：94，90，94.七、八年级抽取的学生竞赛成绩统计表

年级	七年级	八年级
平均数	92	92
中位数	93	b
众数	c	100
方差	52	50.4

根据以上信息，解答下列问题：

(1)、直接写出上述图表中a，b，c的值；

(2)、根据以上数据，你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好？请说明理由（一条理由即可）；

(3)、该校七、八年级共720人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x≥90）的学生人数是多少？

查看试题解析

22. 教科书中这样写道：“我们把多项式a²+2ab+b²及a²﹣2ab+b²叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．
例如：分解因式x²+2x﹣3＝（x²+2x+1）﹣1﹣3＝（x+1）²﹣4＝（x+1+2）（x+1﹣2）＝（x+3）（x﹣1）；例如求代数式2x²+4x﹣6的最小值.2x²+4x﹣6＝2（x²+2x+1）﹣2﹣6＝2（x+1）²﹣8．可知当x＝﹣1时，2x²+4x﹣6有最小值，最小值是﹣8，根据阅读材料用配方法解决下列问题：

(1)、分解因式：m²﹣4m﹣5＝；

(2)、当x为何值时，多项式2x²﹣8x+5有最小值，并求出这个最小值．

查看试题解析
23. 甲、乙两公司全体员工踊跃参与“携手防疫，共渡难关”捐款活动，甲公司共捐款100000元，乙公司共捐款140000元．下面是甲、乙两公司员工的一段对话：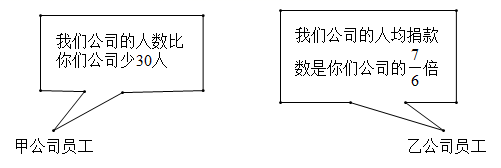

(1)、甲、乙两公司各有多少人？

(2)、现甲、乙两公司共同使用这笔捐款购买 $A$ 、 $B$ 两种防疫物资， $A$ 种防疫物资每箱15000元， $B$ 种防疫物资每箱12000元．若购买 $B$ 种防疫物资不少于10箱，并恰好将捐款用完，有几种购买方案？请设计出来（注： $A$ 、 $B$ 两种防疫物资均需购买，并按整箱配送）．

查看试题解析

锻炼时闭（小时）	5	6	7	8
人数	1	4	3	2

时间/ $h$	1.5	2	2.5	3	3.5	4
人数/人	2	6	6	10	$m$	4