山东省菏泽市郓城县2020-2021学年八级上学期数学期中试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 如图,阴影部分是一个长方形,它的面积是( )
 A、3cm2 B、4cm2 C、5cm2 D、6cm22. 如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为 , , ,则 , , 之间的关系是( )
A、3cm2 B、4cm2 C、5cm2 D、6cm22. 如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为 , , ,则 , , 之间的关系是( )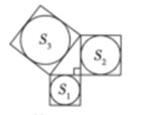 A、 B、 C、 D、无法确定3. 8的平方根是( )A、4 B、±4 C、2 D、4. 下列说法错误的是( )A、如果数轴上的点表示的数不是有理数,那么就一定是无理数 B、大小介于两个有理数之间的无理数有无数个 C、-1的立方是-1,立方根也是-1 D、两个实数,较大者的平方也较大5. 如图,如果“炮”所在位置的坐标为 ,“相”所在位置的坐标为 ,那么“仕”所在位置的坐标为( )
A、 B、 C、 D、无法确定3. 8的平方根是( )A、4 B、±4 C、2 D、4. 下列说法错误的是( )A、如果数轴上的点表示的数不是有理数,那么就一定是无理数 B、大小介于两个有理数之间的无理数有无数个 C、-1的立方是-1,立方根也是-1 D、两个实数,较大者的平方也较大5. 如图,如果“炮”所在位置的坐标为 ,“相”所在位置的坐标为 ,那么“仕”所在位置的坐标为( ) A、 B、 C、 D、6. 已知点 P(-2,3)关于 x 轴的对称点为 Q(a,b),则 a+b 的值是( )A、1 B、-1 C、5 D、-57. 正比例函数y=2x的大致图象是( )A、
A、 B、 C、 D、6. 已知点 P(-2,3)关于 x 轴的对称点为 Q(a,b),则 a+b 的值是( )A、1 B、-1 C、5 D、-57. 正比例函数y=2x的大致图象是( )A、 B、
B、 C、
C、 D、
D、 8. 为了建设社会主义新农村,我市积极推进“行政村通畅工程”.张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间的道路改造.下面能反映该工程尚未改造的道路里程y(公里)与时间x(天)的函数关系的大致图象是( )A、
8. 为了建设社会主义新农村,我市积极推进“行政村通畅工程”.张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间的道路改造.下面能反映该工程尚未改造的道路里程y(公里)与时间x(天)的函数关系的大致图象是( )A、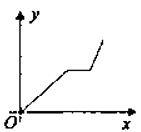 B、
B、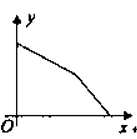 C、
C、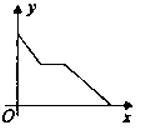 D、
D、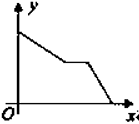
二、填空题
-
9. 如图,在 中, , , ,将 折叠,使点 与点 重合,得折痕 ,则 的周长等于cm.
 10. 如图,数轴上表示数 的点是 .
10. 如图,数轴上表示数 的点是 . 11. 计算: ;12. 如图,平面直角坐标系中有四个点 、 、 、 ,它们的横、纵坐标均为整数.若在此平面直角坐标系内移动点 ,使得这四个点构成的四边形是轴对称图形,并且点 的横、纵坐标仍是整数,则移动后点 的坐标为;
11. 计算: ;12. 如图,平面直角坐标系中有四个点 、 、 、 ,它们的横、纵坐标均为整数.若在此平面直角坐标系内移动点 ,使得这四个点构成的四边形是轴对称图形,并且点 的横、纵坐标仍是整数,则移动后点 的坐标为; 13. 已知y=(2m-1)x3m-2是一次函数,则m= .14. 钓鱼岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是 .
13. 已知y=(2m-1)x3m-2是一次函数,则m= .14. 钓鱼岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是 .
三、解答题
-
15. 已知 , ,求 的值.16. 如图,一根 的电线杆 用铁丝 , 固定,现已知用去的铁丝 , ,又测得地面上 , 两点之间的距离是 , , 两点之间的距离是 ,则电线杆和地面是否垂直,为什么?(提示:要判定电线杆和地面垂直,只需说明 且 即可)
 17. 某消防部队进行消防演练.在模拟现场,有一建筑物发生了火灾,消防车到达后,发现离建筑物的水平距离最近为12 m,如图,即AD=BC=12 m,此时建筑物中距地面12.8 m高的P处有一被困人员需要救援.已知消防云梯车的车身高AB是3.8 m,问此消防车的云梯至少应伸长多少米?
17. 某消防部队进行消防演练.在模拟现场,有一建筑物发生了火灾,消防车到达后,发现离建筑物的水平距离最近为12 m,如图,即AD=BC=12 m,此时建筑物中距地面12.8 m高的P处有一被困人员需要救援.已知消防云梯车的车身高AB是3.8 m,问此消防车的云梯至少应伸长多少米? 18. 如图,四边形ABCD中,AB=AD,∠BAD=90°,若AB=2 ,CD=4 ,BC=8,求四边形ABCD的面积.
18. 如图,四边形ABCD中,AB=AD,∠BAD=90°,若AB=2 ,CD=4 ,BC=8,求四边形ABCD的面积.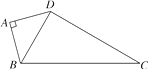 19. 在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(﹣3,1)、(﹣2,﹣3),以及点C的坐标为(3,2)(单位:km).
19. 在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(﹣3,1)、(﹣2,﹣3),以及点C的坐标为(3,2)(单位:km). (1)、请在图中建立直角坐标系并确定点C的位置;(2)、若同学们打算从点B处直接赶往C处,请用方位角和距离描述点C相对于点B的位置.20. 如图,在平面直角坐标系中,正方形ABCD和正方形EFGC面积分别为64和16.
(1)、请在图中建立直角坐标系并确定点C的位置;(2)、若同学们打算从点B处直接赶往C处,请用方位角和距离描述点C相对于点B的位置.20. 如图,在平面直角坐标系中,正方形ABCD和正方形EFGC面积分别为64和16. (1)、请写出点A,E,F的坐标;(2)、求S△BDF .21. 小东从 地出发以某一速度向 地走去,同时小明从 地出发以另一速度向 地走去, , 分别表示小东、小明离 地的距离 与所用时间 的关系,如图所示,根据图象提供的信息,回答下列问题:
(1)、请写出点A,E,F的坐标;(2)、求S△BDF .21. 小东从 地出发以某一速度向 地走去,同时小明从 地出发以另一速度向 地走去, , 分别表示小东、小明离 地的距离 与所用时间 的关系,如图所示,根据图象提供的信息,回答下列问题: (1)、试用文字说明交点 所表示的实际意义;(2)、求 与 的函数关系式;(3)、求小明到达 地所需的时间.22. 某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费.如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.(1)、分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式.(2)、若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨.23. 阅读理解:
(1)、试用文字说明交点 所表示的实际意义;(2)、求 与 的函数关系式;(3)、求小明到达 地所需的时间.22. 某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费.如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.(1)、分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式.(2)、若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨.23. 阅读理解:已知x2- x+1=0,求x2+ 的值.
解:因为x2- x+1=0,所以x2+1= x .
又因为x≠0,所以x+ = .
所以 ,即x2+2+ =5,所以x2+ =3.
请运用以上解题方法,解答下列问题:
已知2m2- m+2=0,求下列各式的值:
(1)、m2+ ;(2)、m- .24. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.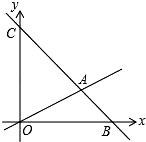 (1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、是否存在点M,使△OMC的面积是△OAC的面积的 ?若存在求出此时点M的坐标;若不存在,说明理由.
(1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、是否存在点M,使△OMC的面积是△OAC的面积的 ?若存在求出此时点M的坐标;若不存在,说明理由.