山东省德州市夏津县2020-2021学年八级上学期数学期中试卷

试卷更新日期：2021-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列命题中错误的是（）

A、全等三角形的对应边相等 B、全等三角形的面积相等 C、全等三角形的周长相等 D、周长相等的两个三角形全等

查看试题解析
3. 如图所示，AB＝CD ， ∠ABD＝∠CDB ，则图中全等三角形共有（）

A、5对 B、4对 C、3对 D、2对

查看试题解析
4. 如图，点 $P$ 在 $∠ A O B$ 的平分线上，点 $P$ 到 $O A$ 边的距离等于5，点 $Q$ 是 $O B$ 边上的任意一点，则下列选项正确的是（）

A、 $P Q \geq 5$ B、 $P Q > 5$ C、 $P Q < 5$ D、 $P Q \leq 5$

查看试题解析
5. 一个等腰三角形的两边长分别是3和7，则它的周长为（）

A、17 B、15 C、13 D、13或17

查看试题解析
6. 如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线。此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是[来（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
7. 如图，在△ABC中，BD平分∠ABC ， ED//BC ，已知AB＝3， AD＝1，则△AED的周长为（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图所示，在等边 $△ A B C$ 中， $D$ 是 $A B$ 的中点， $D E ⊥ A C$ 于 $E$ ， $E F ⊥ B C$ 于 $F$ ，已知 $A B = 8$ ，则 $B F$ 的长为（）

A、3 B、4 C、5 D、6

查看试题解析
9. 如果一个三角形的三个内角都不相等，那么最小角一定小于（）

A、60° B、59° C、45° D、30°

查看试题解析
10. 如图，△ABC的三边AB，BC，CA长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S_△_ABO：S_△_BCO：S_△_CAO等于（）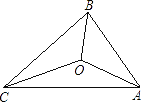

A、1：1：1 B、1：2：3 C、2：3：4 D、3：4：5

查看试题解析
11. 如图，在△ABC中，AD⊥BC ， AE平分∠BAC ，若∠BAE＝30°，∠CAD＝20°，则∠B＝（）

A、45° B、60° C、50° D、55°

查看试题解析
12. 如图，△ABC中，∠C=90°、AD是角平分线，E为AC边上的点，DE=DB，下列结论：①∠DEA＋∠B=180°；② ∠CDE=∠CAB；③ AC= $\frac{1}{2}$ (AB＋AE)；④ S_△_ADC= $\frac{1}{2}$ S_四边形_ABDE ，其中正确的结论个数为（）

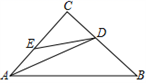A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 如图，要使五边形木架不变形，至少要再钉上根木条.

查看试题解析
14. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ ， $C E ⊥ A B$ ，垂足分别为 $D$ 、 $E$ ，已知 $A B = 8$ ， $A D = 6$ ， $B C = 10$ ，则 $C E =$ ．

查看试题解析
15. 在如图所示的2×2方格中，连接AB、AC，则∠1+∠2=度.

查看试题解析
16. 如图， $∠ 1 = ∠ 2$ ，要使 $△ A B E ≌ △ A C E$ ，还需添加一个条件是：.（填上你认为适当的一个条件即可）

查看试题解析
17. 等腰三角形一腰上的高与另一腰所成的夹角为45°，则这个等腰三角形的顶角度数为 .

查看试题解析
18. 如图，在 $△ A B C$ 中， $E$ 、 $D$ 、 $F$ 分别是 $A D$ 、 $B F$ 、 $C E$ 的中点，若 $△ D E F$ 的面积是1，则 $S_{△ A B C} =$ ．

查看试题解析

三、解答题

19. 在边长为 $1$ 的小正方形组成的正方形网格中建立如图所示的平面直角坐标系，已知格点三角形（ $A B C$ 三角形的三个顶点都在小正方形的顶点上）。

(1)、画出与 $△ A B C$ 关于 $y$ 轴对称的图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、写出 $△ A_{1} B_{1} C_{1}$ 各顶点坐标；

(3)、在（1）的结果下，连接 $B B_{1} ， C C_{1}$ ，求四边形 $B B_{1} C_{1} C$ 的面积。

查看试题解析
20. 如果正多边形的每个内角都比它相邻的外角的4倍多30°．

(1)、它是几边形？

(2)、这个正多边形的内角和是多少度？

(3)、求这个正多边形对角线的条数．

查看试题解析
21. 第十届亚运会在广东召开，有三名运动员分别下榻在 $A$ 、 $B$ 、 $C$ 三个宾馆，三个宾馆由三条道路相连，如图所示．

(1)、为建一个公共活动场地 $P$ 到三个宾馆的距离相等．请用尺规作图方法作出点 $P$ ，使得点 $P$ 落在△ $A B C$ 内部．保留作图痕迹，不要求写作法．

(2)、如果 $∠ A C B = α$ ，那么 $∠ A P B =$ ．

查看试题解析
22. 如图，AB＝AE，BC＝ED，∠B＝∠E，F为CD的中点，说明AF⊥CD的理由．

查看试题解析
23. 如图，点G ， H分别是正六边形ABCDEF的边BC ， CD上的点，且BG=CH ， AG交BH于点P ．

(1)、求证：△ABG≌△BCH；

(2)、
求∠APH的度数．

查看试题解析
24. 如图所示，在△ABC中，∠C＝90°，AD是∠BAC的平分线，DE⊥AB交AB于点E，点F在AC上，BD＝DF.

求证：

(1)、CF＝EB；

(2)、AB＝AF＋2EB.

查看试题解析
25. 在数学探究课上，老师出示了如下探究问题，请你一起来探究．
已知： $C$ 是线段 $A B$ 所在平面内任意一点，分别以 $A C$ 、 $B C$ 为边，在 $A B$ 同侧作等边 $△ A C E$ 和 $△ B C D$ ，连接 $A D$ 、 $B E$ 交于点 $P$ ．

(1)、如图1所示，当点 $C$ 在线段 $A B$ 上移动，线 $A D$ 与 $B E$ 的数量关系是；

(2)、如图2所示，当点 $C$ 在直线 $A B$ ，且 $∠ A C B < 120 °$ ，上面的结论是否还成立？若成立请证明；若不成立，请说明理由．此时 $∠ A P E$ 的大小是否随着 $∠ A C B$ 的大小的变化而发生变化？若变化则写出变化规律，若不变则求出 $∠ A P E$ 的度数；

(3)、如图3所示在（2）的条件下，以 $A B$ 为边在 $A B$ 另一侧作等边 $△ A B F$ ，连接 $A D$ 、 $B E$ 和 $C F$ 交于点 $P$ ，求证： $P B + P C + P A = B E$ ．

查看试题解析