山东省德州市齐河县2020-2021学年八级上学期数学期中试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 下列大学的校徽图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 三角形具有稳定性,就是当三角形的三边长确定时,三角形的形状和大小就确定了,其理论依据是( )A、SAS B、ASA C、AAS D、SSS3. 如图所示,在下列条件中,不能判断 ≌ 的条件是( )
2. 三角形具有稳定性,就是当三角形的三边长确定时,三角形的形状和大小就确定了,其理论依据是( )A、SAS B、ASA C、AAS D、SSS3. 如图所示,在下列条件中,不能判断 ≌ 的条件是( ) A、 , B、 , C、 , D、 ,4. 一个多边形的内角和比它的外角和的3倍少180°,则这个多边形的边数为( )A、5 B、6 C、7 D、85. 平面直角坐标系中,点P(-3,4)关于 轴对称的点的坐标为( )A、(3,4) B、(-3,-4) C、(-3,4) D、(3,-4)6. 为促进旅游发展,某地要在三条公路围成的一块平地上修建一个度假村,如图所示,若要使度假村到三条公路的距离相等,则这个度假村应修建在( )
A、 , B、 , C、 , D、 ,4. 一个多边形的内角和比它的外角和的3倍少180°,则这个多边形的边数为( )A、5 B、6 C、7 D、85. 平面直角坐标系中,点P(-3,4)关于 轴对称的点的坐标为( )A、(3,4) B、(-3,-4) C、(-3,4) D、(3,-4)6. 为促进旅游发展,某地要在三条公路围成的一块平地上修建一个度假村,如图所示,若要使度假村到三条公路的距离相等,则这个度假村应修建在( ) A、三角形 ABC 三条高线的交点处 B、三角形 ABC 三条角平分线的交点处 C、三角形 ABC 三条中线的交点处 D、三角形 ABC 三边垂直平分线的交点处7. 如图,在△ABC中,AC的垂直平分线分别交AB、AC于点D、E,EC=5,△ABC的周长为26,则△BDC的周长为( )
A、三角形 ABC 三条高线的交点处 B、三角形 ABC 三条角平分线的交点处 C、三角形 ABC 三条中线的交点处 D、三角形 ABC 三边垂直平分线的交点处7. 如图,在△ABC中,AC的垂直平分线分别交AB、AC于点D、E,EC=5,△ABC的周长为26,则△BDC的周长为( ) A、14 B、16 C、18 D、198. 下列运算中,正确的是( )A、 B、 C、 D、9. 如果(x2+ax+8)(x2﹣3x+b)展开式中不含x3项,则a的值为( )
A、14 B、16 C、18 D、198. 下列运算中,正确的是( )A、 B、 C、 D、9. 如果(x2+ax+8)(x2﹣3x+b)展开式中不含x3项,则a的值为( )
A、a=3 B、a=﹣3 C、a=0 D、a=110. 下列各式中,运算结果是 的是 ( )A、 B、 C、 D、11. 如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是( )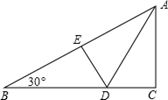 A、12 B、10 C、8 D、612. 如图,∠AOB=30°,点P是∠AOB内的定点,且OP=3.若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
A、12 B、10 C、8 D、612. 如图,∠AOB=30°,点P是∠AOB内的定点,且OP=3.若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )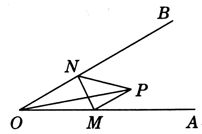 A、12 B、9 C、6 D、3
A、12 B、9 C、6 D、3二、填空题
-
13. 计算: ;若 ,则 .14. 已知一个等腰三角形的一个内角为 ,则它的顶角等于 .15. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为 .
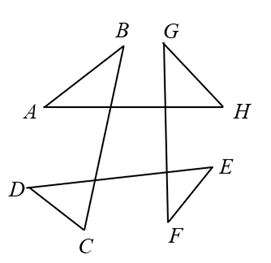 16. 如图,点D是BC上的一点,若△ABC≌△ADE,且∠B=65°,则∠EAC=°.
16. 如图,点D是BC上的一点,若△ABC≌△ADE,且∠B=65°,则∠EAC=°.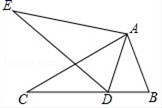 17. 如图,已知∠DAC=68°,依据尺规作图的痕迹,则 = .
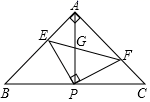
17. 如图,已知∠DAC=68°,依据尺规作图的痕迹,则 = . 18. 如图,在△ABC中,AB=AC , ∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE , PF分别交AB , AC于点E , F , 连接EF交AP于点G . 给出以下四个结论,其中正确的结论是 .
18. 如图,在△ABC中,AB=AC , ∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE , PF分别交AB , AC于点E , F , 连接EF交AP于点G . 给出以下四个结论,其中正确的结论是 .①AE=CF ,
②AP=EF ,
③△EPF是等腰直角三角形,
④四边形AEPF的面积是△ABC面积的一半.
三、解答题
-
19.(1)、计算:
① ;
② ;
③ .
(2)、先化简,再求值: ,其中 .20. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). (1)、请画出△ABC关于x轴成轴对称的图形△A1B1C1 , 并写出A1、B1、C1的坐标;(2)、若小正方形的边长为1,试求△ABC的面积.(3)、在x轴上找一点P , 使PA+PB的值最小,请画出点P的位置.21. 如图,在△ABD和△ACD中,已知AB=AC,∠B=∠C,求证:AD是∠BAC的平分线.
(1)、请画出△ABC关于x轴成轴对称的图形△A1B1C1 , 并写出A1、B1、C1的坐标;(2)、若小正方形的边长为1,试求△ABC的面积.(3)、在x轴上找一点P , 使PA+PB的值最小,请画出点P的位置.21. 如图,在△ABD和△ACD中,已知AB=AC,∠B=∠C,求证:AD是∠BAC的平分线.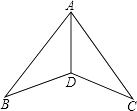 22. 已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
22. 已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF. 23. 如图,在 中, ,点D是 所在直线上一动点,过点D分别作 、 (或其延长线)的垂线,垂足分别为点E、F .
23. 如图,在 中, ,点D是 所在直线上一动点,过点D分别作 、 (或其延长线)的垂线,垂足分别为点E、F .
试问:
(1)、过点C作 边上的高 ,猜想 、 、 的长之间存在怎样的数量关系?并加以证明.(2)、当点D在 的什么位置时, ?并证明.24. 已知等边△ABC , D是BC上一点,E是平面上一点,且DE=AD , ∠ADE=60°,连接CE .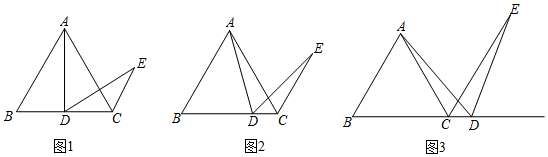 (1)、当点D是线段BC的中点时,如图1.判断线段BD与CE的数量关系,并说明理由;(2)、当点D是线段BC上任意一点时,如图2.请找出线段AB , CE , CD三者之间的数量关系,并说明理由;(3)、当点D在线段BC的延长线上时,如图3,若△ABC边长为6,设CD=x , 则线段CE=(用含x的代数式表示).
(1)、当点D是线段BC的中点时,如图1.判断线段BD与CE的数量关系,并说明理由;(2)、当点D是线段BC上任意一点时,如图2.请找出线段AB , CE , CD三者之间的数量关系,并说明理由;(3)、当点D在线段BC的延长线上时,如图3,若△ABC边长为6,设CD=x , 则线段CE=(用含x的代数式表示).