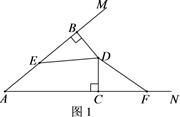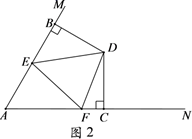山东省滨州市沾化区2020-2021学年八级上学期数学期中试卷
试卷更新日期：2021-09-07 类型：期中考试
一、单选题
-
1. 若一个多边形的内角和为360°，则这个多边形的边数是（ ）A、3 B、4 C、5 D、62. 自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识.下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（ ）A、
B、
C、
D、
3. 三角形的两边长分别为 和 ，则第三边长可能为（ ）A、 B、 C、 D、4. 如图， 是 的外角，若 ， ，则 （ ）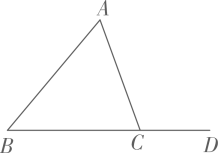
A、 B、 C、 D、5. 如图，将两根钢条AA′、BB′的中点 O连在一起，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是（ ）
A、SAS B、ASA C、SSS D、AAS6. 如果三角形的三个内角的度数比是2：3：5，则它是（ ）A、直角三角形 B、钝角三角形 C、钝角或直角三角形 D、锐角三角形7. 如图，在△ABC中，DE是AC的垂直平分线，AE＝4cm，且△ABD的周长为16cm，则△ABC的周长为（ ）
A、24cm B、22cm C、26cm D、18cm8. 如图，△ABC与△A′B′C′关于直线MN对称，P为MN上任一点（A、P、A′不共线），下列结论中错误的是（ ）
A、△AA′P是等腰三角形 B、MN垂直平分AA′、CC′ C、△ABC与△A′B′C′面积相等 D、直线AB，A′B′的交点不一定在直线MN上9. 如图，△ABC的三边AB、BC、CA长分别是60、70、80，其三条角平分线将△ABC分为三个三角形，则S△ABO：S△BCO：S△CAO等于（ ）
A、1：1：1 B、1：2：3 C、3：7：4 D、6：7：810. 如图在 的两边上截取 ， ，连结 ， 交于点 .则下列结论正确的是（ ）
① ② ③点 在 的平分线上
A、只有① B、只有② C、只有①② D、①②③11. 如图，在△ABC中，∠ABC，∠ACB的平分线BE，CD相交于点F，∠ABC＝42°，∠A＝60°，则∠BFC的度数为（ ）
A、118° B、119° C、120° D、121°12. 如图，△ABC中，∠BAC=90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC.给出下列结论：①∠BAD=∠C； ②∠AEF=∠AFE； ③∠EBC=∠C；④AG⊥EF．正确结论有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
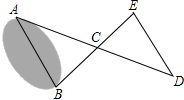
13. 在平面直角坐标系中，点 关于x轴对称的点的坐标是.14. 如图，A、B两点分别位于一个池塘的两端，点C是AD的中点，也是BE的中点，若DE=20米，则AB=米；
15. 如图，已知在△ABD和△ABC中，∠DAB＝∠CAB ， 点A、B、E在同一条直线上，若使△ABD≌△ABC ， 则还需添加的一个条件是 ． （只填一个即可）
16. 一个多边形的内角和与外角和的比是4：1，则它的边数是 ．17. 如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=40°，∠2=20°，则∠B= ．
18. 如图，在 中， ，分别以点A、B为圆心，以大于 的长为半径画弧，两弧分别交于点M、N，作直线 交 点D；以点B为圆心，适当长为半径画弧，分别交 、 于点E、F，再分别以点E、F为圆心，大于 的长为半径画弧，两弧交于点P，作射线 ，此时射线 恰好经过点D，则 度.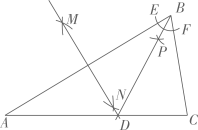
19. 一副直角三角板如上图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，则∠DBC＝°
20. 如图，两条笔直的公路l₁、l₂相交于点O，村庄C的村民在公路的旁边建三个加工厂A，B，D.已知AB=BC=CD=DA=5 km，村庄C到公路l₁的距离为4 km，则村庄C到公路l₂的距离是km.
三、解答题
-
21. 如图在平面直角坐标系中， 顶点的坐标分别为：A(4，0)，B(-1，4)，C(-3，1)
(1)、在图中作 使 和 关于x轴对称；(2)、写出点 的坐标.22. 如图，∠B＝∠E，BF＝EC，AC∥DF．求证：△ABC≌△DEF．
23. 如图，点D是△ABC的边BC上的一点，∠B=∠BAD=∠C，∠ADC=72°．试求∠DAC的度数．
24. 如图，在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在线段BC上，且AE＝CF，连接EF．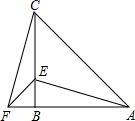
(1)、求证：BE＝BF．(2)、若∠EAC＝30°，则∠CFE是多少度？25. 作图与计算：如图，已知∠AOB及∠AOB内的一点P．
(1)、求作：点P1、点P2 ， 与点P分别关于射线OA、OB对称；(2)、连接P1P2 ， 交OA，OB分别于点E，若P1P2＝12cm，求△PEF的周长．
