江西省抚州市南丰县2020-2021学年八级上学期数学期中试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 下列各数中,是无理数的是( )A、3.1415 B、 C、 D、2. 下列各组数中是勾股数的是( )A、 , , B、3,4,5 C、0.3,0.4,0.5 D、 , ,3. 下列哪个点在函数 的图象上( )A、 B、 C、 D、4. 平面直角坐标系中,点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形6. 如图,在Rt△PQR中,∠PRQ=90°,RP=RQ,边QR在数轴上.点Q表示的数为1,点R表示的数为3,以Q为圆心,QP的长为半径画弧交数轴负半轴于点P1 , 则P1表示的数是( )
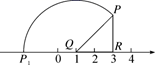 A、-2 B、-2 C、1-2 D、2 -1
A、-2 B、-2 C、1-2 D、2 -1二、填空题
-
7. 比较大小: 3(填“>”、“<”或“=”号)8. 若 +(b+2)2=0,则点M(a,b)关于x轴的对称点的坐标为 .
9. 一次函数 上有两点 和 ,则 (填“ ”“ ”或“ ”).10. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为 .11. 已知一次函数 的图象经过点 且与直线 平行,则此函数的表达式为 .12. 如图所示,在平面直角坐标系中 , ,作 与 全等,则 的坐标 .
三、解答题
-
13. 计算:(1)、 ;(2)、14. 先化简,再求值: ,其中 , .15. 已知 的三边长分别为 、 、 ,且 , , .(1)、判断 的形状,并说明理由;(2)、如果一个正方形的面积与 的面积相等时,求这个正方形的边长.16. 正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。


 17. 已知 的算数平方根是4, 的立方根是3, 是 的整数部分.求 的平方根.18. 如图,直线 与 轴、 轴分别交于点 、 .
17. 已知 的算数平方根是4, 的立方根是3, 是 的整数部分.求 的平方根.18. 如图,直线 与 轴、 轴分别交于点 、 . (1)、求 、 两点的坐标;(2)、在 轴上有一点 ,使得 的面积为 ,求 点的坐标.19. 小慧家与文具店相距 ,小慧从家出发,沿笔直的公路匀速步行 来到文具店买笔记本,停留 ,因家中有事,便沿原路匀速跑步 返回家中.
(1)、求 、 两点的坐标;(2)、在 轴上有一点 ,使得 的面积为 ,求 点的坐标.19. 小慧家与文具店相距 ,小慧从家出发,沿笔直的公路匀速步行 来到文具店买笔记本,停留 ,因家中有事,便沿原路匀速跑步 返回家中. (1)、小慧返回家中的速度比去文具店的速度快多少?(2)、请你画出这个过程中,小慧离家的距离 与时间 的函数图象;(3)、根据图象回答,小慧从家出发后多少分钟离家距离为 ?20. 如图,地面上放着一个小凳子,点 距离墙面 ,在图①中,一根细长的木杆一端与墙角重合,木杆靠在点 处, .在图②中,木杆的一端与点 重合,另一端靠在墙上点 处.
(1)、小慧返回家中的速度比去文具店的速度快多少?(2)、请你画出这个过程中,小慧离家的距离 与时间 的函数图象;(3)、根据图象回答,小慧从家出发后多少分钟离家距离为 ?20. 如图,地面上放着一个小凳子,点 距离墙面 ,在图①中,一根细长的木杆一端与墙角重合,木杆靠在点 处, .在图②中,木杆的一端与点 重合,另一端靠在墙上点 处.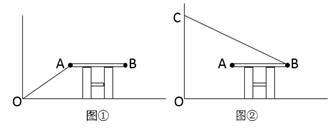 (1)、求小凳子的高度;(2)、若 ,木杆的长度比 长 ,求木杆的长度和小凳子坐板的宽 .21. 如图,平面直角坐标系中, 的顶点都在网格点上,其中 , , .
(1)、求小凳子的高度;(2)、若 ,木杆的长度比 长 ,求木杆的长度和小凳子坐板的宽 .21. 如图,平面直角坐标系中, 的顶点都在网格点上,其中 , , . (1)、作出 关于 轴对称的 ;(2)、求 的面积;(3)、在 轴上是否存在一点 ,使 的和最短?如果存在,请求出此时 的值;如果不存在,请说明理由.22. 如图,MN是一条东西朝向的笔直的公路,C是位于该公路上的一个检测点辆长为9m的小货车BD行驶在该公路上小王位于点A处观察小货车,某时刻他发现车头D、车尾B及检测点C分别距离他10m、17m,2 m
(1)、作出 关于 轴对称的 ;(2)、求 的面积;(3)、在 轴上是否存在一点 ,使 的和最短?如果存在,请求出此时 的值;如果不存在,请说明理由.22. 如图,MN是一条东西朝向的笔直的公路,C是位于该公路上的一个检测点辆长为9m的小货车BD行驶在该公路上小王位于点A处观察小货车,某时刻他发现车头D、车尾B及检测点C分别距离他10m、17m,2 m (1)、过点A向MN引垂线,垂足为E,请利用勾股定理分别找出线段AE与DE、AE与BE之间所满足的数量关系;(2)、在上一问的提示下,继续完成下列问题:
(1)、过点A向MN引垂线,垂足为E,请利用勾股定理分别找出线段AE与DE、AE与BE之间所满足的数量关系;(2)、在上一问的提示下,继续完成下列问题:①求线段DE的长度;
②该小货车的车头D距离检测点C还有多少m?
23. 如图,在平面直角坐标系中, 满足 , ,点 、 分别在 轴和 轴上,当点 从原点 开始沿 轴的正方向运动时,则点 始终落在 轴上运动,点 始终在第一象限运动.
 (1)、当 轴时,求点 的坐标;(2)、随着 、 的运动,当点 落在直线 上时,求此时 点的坐标;(3)、在(2)的条件下,在 轴上是否存在点 ,使以 、 、 、 为顶点的四边形面积是 ?如果存在,请直接写出点 的坐标;如果不存在,请说明理由.
(1)、当 轴时,求点 的坐标;(2)、随着 、 的运动,当点 落在直线 上时,求此时 点的坐标;(3)、在(2)的条件下,在 轴上是否存在点 ,使以 、 、 、 为顶点的四边形面积是 ?如果存在,请直接写出点 的坐标;如果不存在,请说明理由.