江西省吉安市七校联盟2020-2021学年八级上学期数学期中试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 在△ABC中,∠A , ∠B , ∠C所对的边分别为a , b , c , 且∠A:∠B:∠C=1:1:2,则下列说法中,错误的是( )A、∠C=90° B、a=b C、c2=2a2 D、a2=b2﹣c22. 9的算术平方根是( )A、±3 B、3 C、± D、3. 点P(m+1,m﹣2)在x轴上,则点P的坐标为( )
A、(0,﹣3) B、(0,3) C、(3,0) D、(﹣3,0)4. 下列计算正确的是( )A、 B、 C、 D、5. 已知点 、点 在一次函数 的图像上,且 ,则m的取值范围是( )A、 B、 C、 D、6. 直线y=2kx的图象如图所示,则y=(k﹣2)x+1﹣k的图象大致是( ) A、
A、 B、
B、 C、
C、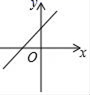 D、
D、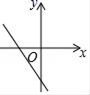
二、填空题
-
7. 点P是第二象限的点且到x轴的距离为3、到y轴的距离为4,则点P的坐标是.8. 若a , b是2020的两个平方根,则2(a+b)﹣ab= .9. 请你写出一个一次函数,满足条件:①经过第一、三、四象限;②与y轴的交点坐标为(0,﹣2),则此一次函数的解析式可以是 .10. 如图,△ABC的边BC在数轴上,点B对应的数字是1,点C对应的数字是2,∠ACB=90°,AC=2,以点B为圆心,AB为半径的圆弧交数轴于点D,则点D所表示的数为 .
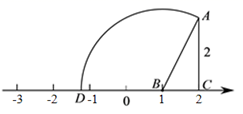 11. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为7 cm,则正方形A , B , C , D的面积之和为cm2 .
11. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为7 cm,则正方形A , B , C , D的面积之和为cm2 . 12. 已知直线y=2x﹣2与x轴交于A , 与y轴交于B , 若点C是坐标轴上的一点,且AC=AB , 则点C的坐标为 .
12. 已知直线y=2x﹣2与x轴交于A , 与y轴交于B , 若点C是坐标轴上的一点,且AC=AB , 则点C的坐标为 .三、解答题
-
13.(1)、( + )2﹣(3 +2 )(3 ﹣2 );(2)、已知点A(a , ﹣3)与点B(5,b)关于x轴对称,求a+b的值.14. 计算: +( +1)2020×(1﹣ )202115. 如图,在3×3的网格中,小正方形的边长为1,连接三个格点得到△ABC .
 (1)、求△ABC的周长.(2)、BC边上的高是多少?16. 水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
(1)、求△ABC的周长.(2)、BC边上的高是多少?16. 水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
图 ① 图②
(1)、容器内原有水多少?(2)、求W与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?17. 图1.2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段 的两个端点均在小正方形的顶点上;
 (1)、在图1中画出以 为底边的等腰直角 ,点 在小正方形顶点上;(2)、在图2中画出以 为腰的等腰 ,点 在小正方形的顶点上,且 的面积为8.18. 如图,在平面直角坐标系中,将矩形ABCD沿直线AE折叠(点E在边DC上),折叠后顶点恰好落在边OC上的点F处,若点D的坐标为(10,8).
(1)、在图1中画出以 为底边的等腰直角 ,点 在小正方形顶点上;(2)、在图2中画出以 为腰的等腰 ,点 在小正方形的顶点上,且 的面积为8.18. 如图,在平面直角坐标系中,将矩形ABCD沿直线AE折叠(点E在边DC上),折叠后顶点恰好落在边OC上的点F处,若点D的坐标为(10,8).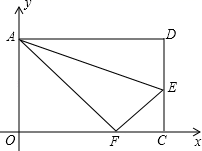 (1)、求CE的长;(2)、写出点E的坐标.19. 如图,过点A(2,0)的两条直线 , 分别交y轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
(1)、求CE的长;(2)、写出点E的坐标.19. 如图,过点A(2,0)的两条直线 , 分别交y轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= . (1)、求点B的坐标;(2)、若△ABC的面积为4,求 的解析式.20. 阅读下面的文字,解答问题:大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,而1< <2,于是可用 ﹣1来表示 的小数部分.请解答下列问题:(1)、 的整数部分是 , 小数部分是;(2)、如果5+ 的小数部分为a , 5﹣ 的整数部分为b , 求a+ b的值.21. 已知点P(x0 , y0)和直线y=kx+b , 则点P到直线y=kx+b的距离可用公式d= 计算.例如求点P(﹣2,1)到直线y=x+1的距离.
(1)、求点B的坐标;(2)、若△ABC的面积为4,求 的解析式.20. 阅读下面的文字,解答问题:大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,而1< <2,于是可用 ﹣1来表示 的小数部分.请解答下列问题:(1)、 的整数部分是 , 小数部分是;(2)、如果5+ 的小数部分为a , 5﹣ 的整数部分为b , 求a+ b的值.21. 已知点P(x0 , y0)和直线y=kx+b , 则点P到直线y=kx+b的距离可用公式d= 计算.例如求点P(﹣2,1)到直线y=x+1的距离.解:由直线y=x+1可知k=1,b=1,d= = = = .
根据以上材料,解答下列问题:
(1)、求点P(2,1)到直线y=2x+1的距离;(2)、求点P(1,1)到直线y=4x﹣3的距离,并说明点P与该直线的位置关系;(3)、已知直线y=﹣x﹣1与直线y=﹣x+3平行,求这两条直线间的距离.22. 如图,在平面直角坐标系中,点C(﹣4,0),点A , B分别在x轴,y轴的正半轴上,且满足 +|OA﹣1|=0 (1)、写点A、B的坐标及直线AB的解析式;(2)、在x轴上是否存在点D , 使以点B、C、D为顶点的三角形的面积S△BCD= S△ABC?若存在,请写出点D的坐标;若不存在,请说明理由.23. 如图
(1)、写点A、B的坐标及直线AB的解析式;(2)、在x轴上是否存在点D , 使以点B、C、D为顶点的三角形的面积S△BCD= S△ABC?若存在,请写出点D的坐标;若不存在,请说明理由.23. 如图 (1)、问题探究
(1)、问题探究①如图1,在直角△ABC中,∠BAC=90°,BC=13,AB=5,若P是BC边上一动点,连接AP , 求AP的最小值.
②如图2,在等腰直角△ABC中,∠ABC=90°,AC=a , 求边AB的长度(用含a的代数式表示).
(2)、问题解决如图3,在等腰直角△ABC中,∠ABC=90°,AC=4,D是边BC的中点,若P是AB边上一动点,E是AC边上一动点,请直接写出PD+PE的最小值.