辽宁省盘锦市2021年中考数学试卷
试卷更新日期:2021-09-07 类型:中考真卷
一、单选题
-
1. 3的相反数是( )A、 3 B、-3 C、 D、2.
图中三视图对应的正三棱柱是( )
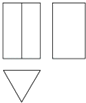 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 空气是由多种气体混合而成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是( )A、条形图 B、扇形图 C、折线图 D、频数分布直方图5. 下列命题正确的是( )A、同位角相等 B、相等的圆心角所对的弧相等 C、对角线相等的四边形是矩形 D、直角三角形斜边上的中线等于斜边的一半6. 下列调查中,适宜采用抽样调查的是( )A、调查某班学生的身高情况 B、调查亚运会100m游泳决赛运动员兴奋剂的使用情况 C、调查某批汽车的抗撞击能力 D、调查一架“歼10”隐形战斗机各零部件的质量7. 如图,已知直线AB和AB上的一点C , 过点C作直线AB的垂线,步骤如下:
3. 下列运算正确的是( )A、 B、 C、 D、4. 空气是由多种气体混合而成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是( )A、条形图 B、扇形图 C、折线图 D、频数分布直方图5. 下列命题正确的是( )A、同位角相等 B、相等的圆心角所对的弧相等 C、对角线相等的四边形是矩形 D、直角三角形斜边上的中线等于斜边的一半6. 下列调查中,适宜采用抽样调查的是( )A、调查某班学生的身高情况 B、调查亚运会100m游泳决赛运动员兴奋剂的使用情况 C、调查某批汽车的抗撞击能力 D、调查一架“歼10”隐形战斗机各零部件的质量7. 如图,已知直线AB和AB上的一点C , 过点C作直线AB的垂线,步骤如下:第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以 为半径作弧,两弧交于点F;
第三步:作直线CF , 直线CF即为所求.
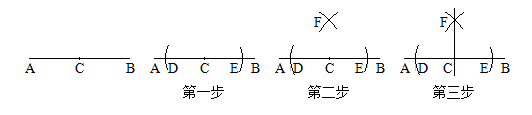
下列关于 的说法正确的是( )
A、 ≥ B、 ≤ C、 D、8. “今有井径五尺,不知其深,立五尺木于井上,从末望水岸,入径四寸,问井深几何?”这是我国古代数学著作《九章算术》中的“井深几何”问题,它的题意可以由示意图获得.设井深为 尺,所列方程正确的是( )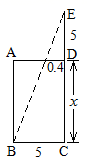 A、 B、 C、 D、9. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( )
A、 B、 C、 D、9. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( )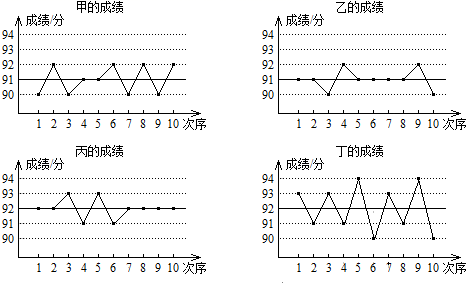 A、甲 B、乙 C、丙 D、丁10. 如图,四边形ABCD是菱形,BC=2,∠ABC=60°,对角线AC与BD相交于点O , 线段BD沿射线AD方向平移,平移后的线段记为PQ , 射线PQ与射线AC交于点M , 连结PC , 设OM长为 ,△PMC面积为 .下列图象能正确反映出 与 的函数关系的是( )
A、甲 B、乙 C、丙 D、丁10. 如图,四边形ABCD是菱形,BC=2,∠ABC=60°,对角线AC与BD相交于点O , 线段BD沿射线AD方向平移,平移后的线段记为PQ , 射线PQ与射线AC交于点M , 连结PC , 设OM长为 ,△PMC面积为 .下列图象能正确反映出 与 的函数关系的是( )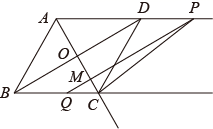 A、
A、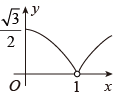 B、
B、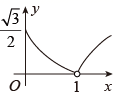 C、
C、 D、
D、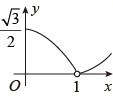
二、填空题
-
11. 建党100周年期间,我市人社系统不断提升服务能力和水平,让我市约1 300 000参保人员获得更高质量的社会保障福祉.数据1 300 000用科学记数法表示为12. 分解因式: =13. 计算: =14. 从不等式组 的所有整数解中任取一个数,它是偶数的概率是15. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2
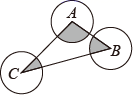 16. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是
16. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是 17. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E , 分别以点C , E为圆心,大于 的长为半径作弧,两弧交于点P , 作射线BP交AD的延长线于点F , ∠CBE=60°,BC=6,则BF的长为
17. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E , 分别以点C , E为圆心,大于 的长为半径作弧,两弧交于点P , 作射线BP交AD的延长线于点F , ∠CBE=60°,BC=6,则BF的长为 18. 如图,四边形ABCD为矩形,AB= ,AD= ,点P为边AB上一点.以DP为折痕将△DAP翻折,点A的对应点为点A'.连结AA',AA' 交PD于点M , 点Q为线段BC上一点,连结AQ , MQ , 则AQ+MQ的最小值是
18. 如图,四边形ABCD为矩形,AB= ,AD= ,点P为边AB上一点.以DP为折痕将△DAP翻折,点A的对应点为点A'.连结AA',AA' 交PD于点M , 点Q为线段BC上一点,连结AQ , MQ , 则AQ+MQ的最小值是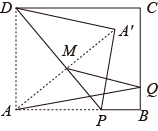
三、解答题
-
19. 先化简,再求值: ,其中20. 某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;
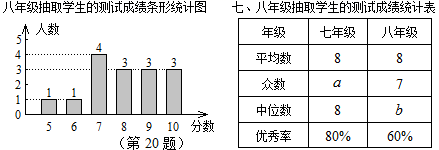 (1)、填空: = , =;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.21. 如图,直线 交 轴于点M , 四边形OMAE是矩形,S矩形OMAE=4,反比例函数 的图象经过点A , EA的延长线交直线 于点D .
(1)、填空: = , =;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.21. 如图,直线 交 轴于点M , 四边形OMAE是矩形,S矩形OMAE=4,反比例函数 的图象经过点A , EA的延长线交直线 于点D .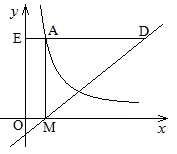 (1)、求反比例函数的解析式;(2)、若点B在 轴上,且AB=AD , 求点B的坐标.22. 如图,小华遥控无人机从点A处飞行到对面大厦MN的顶端M , 无人机飞行方向与水平方向的夹角为37°,小华在点A测得大厦底部N的俯角为31°,两楼之间一棵树EF的顶点E恰好在视线AN上,已知树的高度为6米,且 ,楼AB , MN , 树EF均垂直于地面,问:无人机飞行的距离AM约是多少米?(结果保留整数.参考数据:cos31°≈0.86, tan31°≈0.60, cos37°≈0.80, tan37°≈0.75)
(1)、求反比例函数的解析式;(2)、若点B在 轴上,且AB=AD , 求点B的坐标.22. 如图,小华遥控无人机从点A处飞行到对面大厦MN的顶端M , 无人机飞行方向与水平方向的夹角为37°,小华在点A测得大厦底部N的俯角为31°,两楼之间一棵树EF的顶点E恰好在视线AN上,已知树的高度为6米,且 ,楼AB , MN , 树EF均垂直于地面,问:无人机飞行的距离AM约是多少米?(结果保留整数.参考数据:cos31°≈0.86, tan31°≈0.60, cos37°≈0.80, tan37°≈0.75) 23. 如图,△ABC内接于⊙O , AB是⊙O的直径,过⊙O外一点D作 ,DG交线段AC于点G , 交AB于点E , 交⊙O于点F , 连接DB , CF , ∠A=∠D .
23. 如图,△ABC内接于⊙O , AB是⊙O的直径,过⊙O外一点D作 ,DG交线段AC于点G , 交AB于点E , 交⊙O于点F , 连接DB , CF , ∠A=∠D .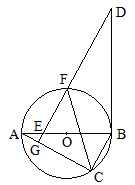 (1)、求证:BD与⊙O相切;(2)、若AE=OE , CF平分∠ACB , BD=12,求DE的长.24. 某工厂生产并销售A , B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床 台.(1)、当 时,完成以下两个问题:
(1)、求证:BD与⊙O相切;(2)、若AE=OE , CF平分∠ACB , BD=12,求DE的长.24. 某工厂生产并销售A , B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床 台.(1)、当 时,完成以下两个问题:①请补全下面的表格:
A型
B型
车床数量/台
▲
每台车床获利/万元
10
▲
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)、当0< ≤14时,设生产并销售A , B两种型号车床获得的总利润为W万元,如何分配生产并销售A , B两种车床的数量,使获得的总利润W最大?并求出最大利润.25. 如图,四边形ABCD是正方形,△ECF为等腰直角三角形,∠ECF=90°,点E在BC上,点F在CD上,N为EF的中点,连结NA , 以NA , NF为邻边作▱ANFG.连结DG , DN , 将Rt△ECF绕点C顺时针方向旋转,旋转角为 (0°≤ ≤360°).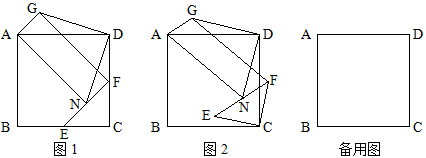 (1)、如图1,当 =0°时,DG与DN的关系为;(2)、如图2,当 时,(1)中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、在Rt△ECF旋转的过程中,当▱ANFG的顶点G落在正方形ABCD的边上,且AB=12,EC= 时,连结GN , 请直接写出GN的长.26. 如图,抛物线 与 轴交于A , B两点(点A在点B的左侧),与 轴交于点C , 直线 与 轴交于点D , 与 轴交于点E , 与直线BC交于点F .
(1)、如图1,当 =0°时,DG与DN的关系为;(2)、如图2,当 时,(1)中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、在Rt△ECF旋转的过程中,当▱ANFG的顶点G落在正方形ABCD的边上,且AB=12,EC= 时,连结GN , 请直接写出GN的长.26. 如图,抛物线 与 轴交于A , B两点(点A在点B的左侧),与 轴交于点C , 直线 与 轴交于点D , 与 轴交于点E , 与直线BC交于点F .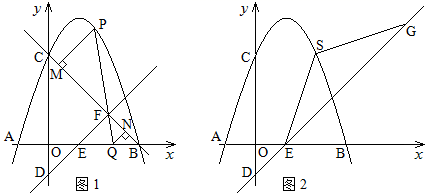 (1)、点F的坐标是;(2)、如图1,点P为第一象限抛物线上的一点,PF的延长线交OB于点Q , PM⊥BC于点M , QN⊥BC于点N , ,求点P的坐标;(3)、如图2,点S为第一象限抛物线上的一点,且点S在射线DE上方,动点G从点E出发,沿射线DE方向以每秒 个单位长度的速度运动,当SE=SG , 且 时,求点G的运动时间.
(1)、点F的坐标是;(2)、如图1,点P为第一象限抛物线上的一点,PF的延长线交OB于点Q , PM⊥BC于点M , QN⊥BC于点N , ,求点P的坐标;(3)、如图2,点S为第一象限抛物线上的一点,且点S在射线DE上方,动点G从点E出发,沿射线DE方向以每秒 个单位长度的速度运动,当SE=SG , 且 时,求点G的运动时间.