初中数学浙教版九年级上册第4章 相似三角形单元检测
试卷更新日期:2021-09-07 类型:单元试卷
一、单选题
-
1. 如图所示的两个四边形相似,则α的度数是( )
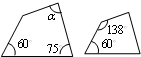 A、60° B、75° C、87° D、120°2. 已知 (a≠0,b≠0),下列变形正确的是( )A、 B、 C、 D、3. 如图,已知 , , , ,则 的长是( )
A、60° B、75° C、87° D、120°2. 已知 (a≠0,b≠0),下列变形正确的是( )A、 B、 C、 D、3. 如图,已知 , , , ,则 的长是( ) A、5 B、6 C、15 D、204. 如图,点G、F分别是 的边 、 上的点, 的延长线与 的延长线相交于点A , 交 于点E , 则下列结论错误的是( )
A、5 B、6 C、15 D、204. 如图,点G、F分别是 的边 、 上的点, 的延长线与 的延长线相交于点A , 交 于点E , 则下列结论错误的是( )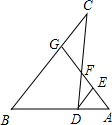 A、 B、 C、 D、5. 如图,在4×4的正方形网格中,画2个相似三角形,在下列各图中,正确的画法有( )
A、 B、 C、 D、5. 如图,在4×4的正方形网格中,画2个相似三角形,在下列各图中,正确的画法有( ) A、1个 B、2个 C、3个 D、4个6. 如图, 中, , ,点 在 的延长线上,且 连接 并延长,过 作 于点 ,若 ,则 的面积为( )
A、1个 B、2个 C、3个 D、4个6. 如图, 中, , ,点 在 的延长线上,且 连接 并延长,过 作 于点 ,若 ,则 的面积为( )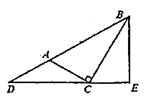 A、1 B、2 C、 D、7. 如图,线段AB∥CD,连接AD,BC交于点O,若CD=2AB,则下列选项中错误的是( )
A、1 B、2 C、 D、7. 如图,线段AB∥CD,连接AD,BC交于点O,若CD=2AB,则下列选项中错误的是( )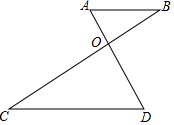 A、△AOB∽△DOC B、 C、 D、8. 在边长为 的正方形 中,对角线 与 相交于点O , P是 上一动点,过P作 ,分别交正方形的两条边于点E , F . 设 , 的面积为y , 当 时,y与x之间的关系式为( )
A、△AOB∽△DOC B、 C、 D、8. 在边长为 的正方形 中,对角线 与 相交于点O , P是 上一动点,过P作 ,分别交正方形的两条边于点E , F . 设 , 的面积为y , 当 时,y与x之间的关系式为( ) A、 B、 C、 D、9. 如图,E , F分别为矩形ABCD的边AD , BC的中点,若矩形ABCD与矩形EABF相似,AB=1,则矩形ABCD的面积是( )
A、 B、 C、 D、9. 如图,E , F分别为矩形ABCD的边AD , BC的中点,若矩形ABCD与矩形EABF相似,AB=1,则矩形ABCD的面积是( )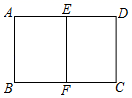 A、4 B、2 C、 D、10. 如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
A、4 B、2 C、 D、10. 如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )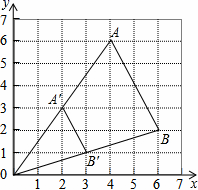 A、 B、(m,n) C、 D、
A、 B、(m,n) C、 D、二、填空题
-
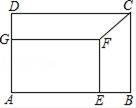
11. 在平面直角坐标系中已知点 , ,以原点 为位似中心,相似比为1:2,将 扩大,则点 的对应点 的坐标是 .12. 如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为 ,连接CF,则CF=.
 13. 如图,已知每个小方格的边长均为1,则 与 的周长比为 .
13. 如图,已知每个小方格的边长均为1,则 与 的周长比为 .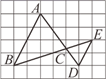 14. 如图,在△ABC中,∠C=90°,BC=16 cm,AC=12 cm,点P从点B出发,沿BC以2 cm/s的速度向点C移动,点Q从点C出发,以1 cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=时,△CPQ与△CBA相似.
14. 如图,在△ABC中,∠C=90°,BC=16 cm,AC=12 cm,点P从点B出发,沿BC以2 cm/s的速度向点C移动,点Q从点C出发,以1 cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=时,△CPQ与△CBA相似.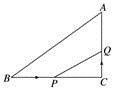 15. 如图, ,相似比为 ,则面积之比 为 .
15. 如图, ,相似比为 ,则面积之比 为 .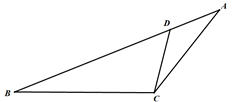 16. 如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为.
16. 如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为.
三、解答题
-
17. 如图, 是 的角平分线,延长 至点 使得 .求证: .
 18. 已知直线l1∥l2∥l3 , AG=1.2cm,BG=2.4cm,EF=3cm,CD=4cm,求CH、KF的值。
18. 已知直线l1∥l2∥l3 , AG=1.2cm,BG=2.4cm,EF=3cm,CD=4cm,求CH、KF的值。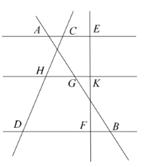 19. 如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
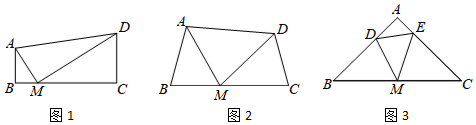
19. 如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.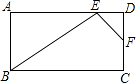 20.(1)、体验:如图1,在四边形ABCD中,AB∥CD , ∠B=90°,点M在BC边上,当∠AMD=90°时,可知△ABM△MCD(不要求证明).(2)、探究:如图2,在四边形ABCD中,点M在BC上,当∠B=∠C=∠AMD时,求证:△ABM∽△MCD .
20.(1)、体验:如图1,在四边形ABCD中,AB∥CD , ∠B=90°,点M在BC边上,当∠AMD=90°时,可知△ABM△MCD(不要求证明).(2)、探究:如图2,在四边形ABCD中,点M在BC上,当∠B=∠C=∠AMD时,求证:△ABM∽△MCD .拓展:如图3,在△ABC中,点M是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DME=45°,BC=8 ,CE=6,求DE的长.
 21. 一个矩形ABCD的较短边长为2.
21. 一个矩形ABCD的较短边长为2.(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
 22. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
22. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2 , 并写出C2的坐标.
四、综合题
-
23. 如图1, 是 的高, .
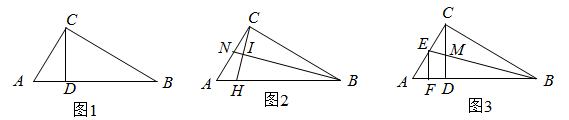 (1)、求证: .(2)、如图2, 是 的中线, 于点I交 于H点,若 ,求 的值.(3)、如图3,M是 的中点, 交 于E, 于F.若 , ,直接写出 的值.24. 汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,△ABC、△FED分别为汽车两侧盲区的示意图,已知视线PB与地面BE的夹角∠PBE=43°,视线PE与地面BE的夹角∠PEB=20°,点A,F分别为PB,PE与车窗底部的交点,AF∥BE,AC,FD垂直地面BE,A点到B点的距离AB=1.6m.
(1)、求证: .(2)、如图2, 是 的中线, 于点I交 于H点,若 ,求 的值.(3)、如图3,M是 的中点, 交 于E, 于F.若 , ,直接写出 的值.24. 汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,△ABC、△FED分别为汽车两侧盲区的示意图,已知视线PB与地面BE的夹角∠PBE=43°,视线PE与地面BE的夹角∠PEB=20°,点A,F分别为PB,PE与车窗底部的交点,AF∥BE,AC,FD垂直地面BE,A点到B点的距离AB=1.6m.(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)
 (1)、求盲区中DE的长度;(2)、点M在ED上,MD=1.8m,在M处有一个高度为0.3m的物体,驾驶员能观察到物体吗?请说明理由。25. 在梯形 中, , , ,对角线 和 相交于点 ,等腰直角 的直角顶点 与梯形的顶点 重合,将 绕点 旋转
(1)、求盲区中DE的长度;(2)、点M在ED上,MD=1.8m,在M处有一个高度为0.3m的物体,驾驶员能观察到物体吗?请说明理由。25. 在梯形 中, , , ,对角线 和 相交于点 ,等腰直角 的直角顶点 与梯形的顶点 重合,将 绕点 旋转 (1)、如图1,当 的一边 落在 边上,另一边 落在 边的延长线上时,求证:(2)、继续旋转 ,旋转角为 ,请你在图2中画出图形,并判断(1)中的结论是否成立?若成立加以证明:若不成立,说明理由;(3)、如图3,继续旋转 ,当三角形的一边 与梯形对角线 重合, 与 相交于点 时,若 , , ,分别求出线段 、 、 的长.
(1)、如图1,当 的一边 落在 边上,另一边 落在 边的延长线上时,求证:(2)、继续旋转 ,旋转角为 ,请你在图2中画出图形,并判断(1)中的结论是否成立?若成立加以证明:若不成立,说明理由;(3)、如图3,继续旋转 ,当三角形的一边 与梯形对角线 重合, 与 相交于点 时,若 , , ,分别求出线段 、 、 的长.