初中数学浙教版九年级上册4.6 相似多边形同步练习
试卷更新日期：2021-09-07 类型：同步测试
一、单选题
-
1. 如图，把一个矩形分割成四个全等的小矩形，要使小矩形与原矩形相似，则原矩形的长与宽之比为（ ）
A、2：1 B、4：1 C、 D、1：22. 如果两个相似多边形的面积之比为1：4，那么它们的周长之比是( ）
A、1：2 B、1：4 C、1：8 D、1：163. 如图，在平面直角坐标系中，矩形 与矩形 是以点 为位似中心的位似图形，点 的坐标为 ，若 ，则 的长是（ ）
A、3 B、4 C、4.5 D、64. 一个五边形的边长分别为2，3，4，5，6，另一个和它相似的五边形的最长边长为24，则这个五边形的最短边长为（ ）A、6 B、8 C、12 D、105. 如图，一张矩形报纸ABCD的长AB=a，宽BC=b，E，F分别是AB，CD的中点，将这张报纸沿着直线EF对折后，矩形AEFD的长与宽的比等于矩形ABCD的长与宽的比，则a：b等于（ ）
A、 B、 C、 D、6. 用放大镜观察一个五边形时，不变的量是（ ）A、各边的长度 B、各内角的度数 C、五边形的周长 D、五边形的面积7. 若将一个正方形的各边长扩大为原来的4倍，则这个正方形的面积扩大为原来的（ ）A、16倍 B、8倍 C、4倍 D、2倍8. 如果一个矩形对折后所得矩形与原矩形相似，则此矩形的长边与短边的比是（ ）A、1： B、 ：1 C、2：1 D、4：19. 如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（ ）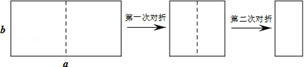
A、a＝ b B、a＝2b C、a＝2 b D、a＝4b10. 书画经装裱后更便于收藏．如图，画心ABCD为长90cm、宽30cm的矩形，装裱后整幅画为矩形A′B′C′D′，两矩形的对应边互相平行，且AB与A′B'的距离、CD与C′D′的距离都等于4cm ． 当AD与A′D′的距离、BC与B'C′距离都等于acm ， 且矩形ABCD∽矩形A′B′C′D'时，整幅书画最美观此时，a的值为（ ）
A、4 B、6 C、12 D、24二、填空题
-
11. 下列五组图形中，①两个等腰三角形；②两个等边三角形；③两个菱形；④两个矩形；⑤两个正方形．一定相似的有（填序号）12. 一个四边形的边长分别是3，4，5，6，另一个与它相似的四边形最小边长为6，则另一个四边形的最长边是.13. 两个相似多边形的面积比是9：16，其中较小多边形周长为36cm，则较大多边形周长为 ．14. 一个多边形的边长依次为1，2，3，4，5，6，与它相似的另一个多边形的最大边长为8，那么另一个多边形的周长是.15. 把一个长方形按如图方式划分成三个全等的小长方形，每一个小长方形与原长方形相似，若小长方形的宽为2，则原长方形的宽x为。
16. 秋天红透的枫叶，总能牵动人们无尽的思绪，所以诗人杜牧说：“停车坐爱枫林晚，霜叶红于二月花”如图是两片形状完全相同，大小不同的枫叶，则 的值为 ．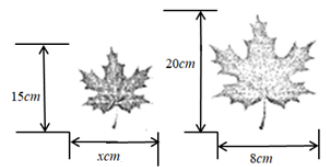
三、解答题
-
17. 如图，已知矩形ABCD与矩形DEFC相似，且AB＝2 cm，BC＝5 cm，求AE的长．
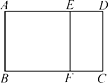18. 在一块长和宽分别为3m和2m的矩形塑料板四周镶上木条．若在长边上镶上的木条的宽为0.5m．则要使木条内缘围成的矩形与木条外缘围成的矩形相似，在宽边上镶的木条的宽应是多少？
19. 如图，已知四边形ABCD相似于四边形A′B′C′D′，求∠A的度数及x的值．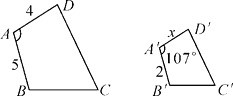
20. 如图，△ABC中，AB=8厘米，AC=16厘米，点P从A出发，以每秒2厘米的速度向B运动，点Q从C同时出发，以每秒3厘米的速度向A运动，其中一个动点到端点时，另一个动点也相应停止运动，那么，当以A、P、Q为顶点的三角形与△ABC相似时，运动时间是多少？
21. 如图，四边形ABCD和四边形EFGH相似，求∠α、∠β的大小和EH的长度．
四、综合题
-
22. 一个矩形ABCD的较短边长为2．
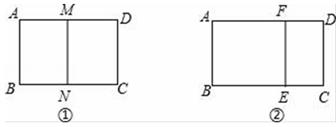(1)、如图①，若沿长边对折后得到的矩形与原矩形相似，求它的另一边长；(2)、如图②，已知矩形ABCD的另一边长为4，剪去一个矩形ABEF后，余下的矩形EFDC与原矩形相似，求余下矩形EFDC的面积．23. 图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列)，∠A＝∠D1＝135°，∠B＝∠E1＝120°，∠C1＝95°.
(1)、求∠F的度数；(2)、如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1：1.5，且CD＝15cm，求C1D1的长度．24. 如图，把矩形ABCD对折，折痕为MN， 矩形DMNC与矩形ABCD相似，已知AB=4．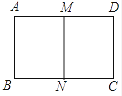
(1)、求AD的长；(2)、求矩形DMNC与矩形ABCD的相似比．25. 如图，把矩形ABCD对折，折痕为MN，矩形DMNC与矩形ABCD相似，已知AB＝4.
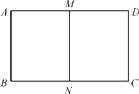(1)、求AD的长；(2)、求矩形DMNC与矩形ABCD的相似比．26. 阅读下列材料，完成任务：自相似图形
定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．
任务：
(1)、图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为；(2)、如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为；(3)、现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．请从下列A、B两题中任选一条作答．
A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=（用含b的式子表示）；
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=（用含n，b的式子表示）；
B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含b的式子表示）；
②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含m，n，b的式子表示）．