初中数学浙教版九年级上册4.5 相似三角形的性质及应用同步练习
试卷更新日期:2021-09-07 类型:同步测试
一、单选题
-
1. 如图,在 中, ,且 ,则 的值为( )
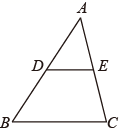 A、 B、 C、 D、2. 如图所示,在△ABC 中,AB=6,AC=4,P 是AC 的中点,过 P 点的直线交AB 于点Q,若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ 的长为 ( )
A、 B、 C、 D、2. 如图所示,在△ABC 中,AB=6,AC=4,P 是AC 的中点,过 P 点的直线交AB 于点Q,若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ 的长为 ( )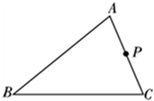 A、3 B、3或 C、3或 D、3. 如图,□ABCD中,EF∥AB,DE∶DA = 2∶5,EF = 4,则CD的长为( )
A、3 B、3或 C、3或 D、3. 如图,□ABCD中,EF∥AB,DE∶DA = 2∶5,EF = 4,则CD的长为( ) A、 B、8 C、10 D、164. 如图,在 和 中, , , .连接CD , 连接BE并延长交AC , AD于点F , G . 若BE恰好平分 ,则下列结论错误的是( )
A、 B、8 C、10 D、164. 如图,在 和 中, , , .连接CD , 连接BE并延长交AC , AD于点F , G . 若BE恰好平分 ,则下列结论错误的是( )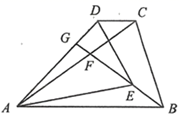 A、 B、 C、 D、5. 如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为( )
A、 B、 C、 D、5. 如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为( ) A、12米 B、12.5米 C、14米 D、15米6. 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m , n),则大三角形中与之对应的顶点坐标为( )
A、12米 B、12.5米 C、14米 D、15米6. 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m , n),则大三角形中与之对应的顶点坐标为( ) A、(﹣2m , ﹣2n) B、(2m , 2n) C、(﹣2n , ﹣2m) D、(2n , 2m)7. 如图,四边形 中, 为对角线 上一点,过点 作 ,交 于点 ,过点 作 ,交 于点 ,则下列所给的结论中,不一定正确的是( ).
A、(﹣2m , ﹣2n) B、(2m , 2n) C、(﹣2n , ﹣2m) D、(2n , 2m)7. 如图,四边形 中, 为对角线 上一点,过点 作 ,交 于点 ,过点 作 ,交 于点 ,则下列所给的结论中,不一定正确的是( ).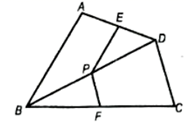 A、 B、 C、 D、8. 如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( )
A、 B、 C、 D、8. 如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( ) A、1:2 B、1:3 C、2:3 D、3:49. 如图,在平行四边形 中, , , 的面积为25,则四边形 的面积为( )
A、1:2 B、1:3 C、2:3 D、3:49. 如图,在平行四边形 中, , , 的面积为25,则四边形 的面积为( ) A、25 B、9 C、21 D、1610. 如图,在 中, ,将 绕点 顺时针旋转,使点 旋转至 边上的点 处,点 的对应点为点 , 的延长线恰好经过点 ,则 的长为( )
A、25 B、9 C、21 D、1610. 如图,在 中, ,将 绕点 顺时针旋转,使点 旋转至 边上的点 处,点 的对应点为点 , 的延长线恰好经过点 ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
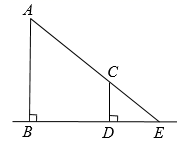
11. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.
 12. 如图,在△ABC中,E , F分别是AB , AC上的点,且满足AE AB , AF AC , BC=4,则EF的值为 .
12. 如图,在△ABC中,E , F分别是AB , AC上的点,且满足AE AB , AF AC , BC=4,则EF的值为 .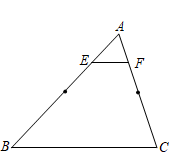 13. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 ,从木杆的顶端B观察井水水岸D , 视线 与井口的直径 交于点E , 如果测得 米, 米, 米,那么 为米.
13. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 ,从木杆的顶端B观察井水水岸D , 视线 与井口的直径 交于点E , 如果测得 米, 米, 米,那么 为米.
 14. 如图,在平面直角坐标系中,A(4,0),B(-2,0),C(4,4),D(﹣2,6),点E在x轴上,满足∠BED=∠AEC,则点E的坐标为.
14. 如图,在平面直角坐标系中,A(4,0),B(-2,0),C(4,4),D(﹣2,6),点E在x轴上,满足∠BED=∠AEC,则点E的坐标为. 15. 如图,在 中, , 是 中点, 是 上一点, , ,则 的长为 .
15. 如图,在 中, , 是 中点, 是 上一点, , ,则 的长为 .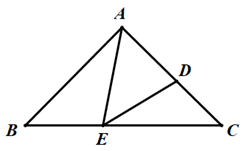 16. 如图,在 中, ,垂足为 , , ,四边形 和四边形 均为正方形,且点 、 、 、 、 、 都在 的边上,那么 与四边形 的面积比为 .
16. 如图,在 中, ,垂足为 , , ,四边形 和四边形 均为正方形,且点 、 、 、 、 、 都在 的边上,那么 与四边形 的面积比为 .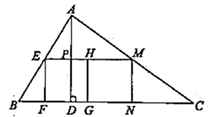
三、解答题
-
17. 如图,在直角三角形 中, ,作 的内接矩形 .设 ,求x取何值时矩形的面积最大?
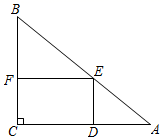 18. 清朝《数理精蕴》里有一首小诗《古色古香方城池》:今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?
18. 清朝《数理精蕴》里有一首小诗《古色古香方城池》:今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?如图所示,诗的意思是:有正方形的城池一座,四面城墙的正中有门,从南门口(点D)直行8里有一塔(点A),自西门(点E)直行2里至点B,切城角(点C)也可以看见塔,问这座方城每面城墙的长是多少里?
 19. 如图,已知 ,求证: .
19. 如图,已知 ,求证: .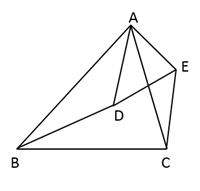 20. 小雁塔位于西安市南郊的荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.数学活动小组的同学对该塔进行了测量,测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为38米,塔的顶端为点A,且 ,在点E处竖直放一根标杆,其顶端为D, ,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得 米.已知标杆 米,求该塔的高度AB.
20. 小雁塔位于西安市南郊的荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.数学活动小组的同学对该塔进行了测量,测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为38米,塔的顶端为点A,且 ,在点E处竖直放一根标杆,其顶端为D, ,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得 米.已知标杆 米,求该塔的高度AB.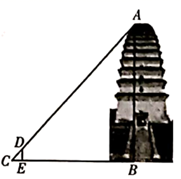
四、综合题
-
21. 如图所示,△ABC中,BD⊥AC于点D , CE⊥AB于点E , BD与CE相交于点F .
 (1)、求证:△BEF∽△CDF;(2)、求证:DE·BF=EF·BC .22. 如图,在 中,点 、 分别在边 , 上, ,线段 分别交线段 , 于点 , ,且 .
(1)、求证:△BEF∽△CDF;(2)、求证:DE·BF=EF·BC .22. 如图,在 中,点 、 分别在边 , 上, ,线段 分别交线段 , 于点 , ,且 .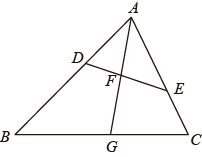 (1)、求证: ;(2)、若 ,求 的值.23. 如图,在 和 中, , .
(1)、求证: ;(2)、若 ,求 的值.23. 如图,在 和 中, , . (1)、求证: ;(2)、若 , ,求 的长.24. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G,且
(1)、求证: ;(2)、若 , ,求 的长.24. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G,且 (1)、求证:△ADF∽△ACG;(2)、若 ,求 的值。25. 已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,点F在边AB上,BC2=BF•BA,CF与DE相交于点G.
(1)、求证:△ADF∽△ACG;(2)、若 ,求 的值。25. 已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,点F在边AB上,BC2=BF•BA,CF与DE相交于点G.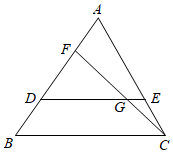 (1)、求证:△BCF∽△DGF;(2)、求证:DF•AB=BC•DG;(3)、当点E为AC中点时,求证:2DF•EG=AF•DG.
(1)、求证:△BCF∽△DGF;(2)、求证:DF•AB=BC•DG;(3)、当点E为AC中点时,求证:2DF•EG=AF•DG.

