初中数学浙教版九年级上册4.2 由平行线截得的比例线段同步练习
试卷更新日期:2021-09-07 类型:同步测试
一、单选题
-
1. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( )
 A、 B、 C、 D、2. 如图,已知直线AB∥CD∥EF , BD=2,DF=4,则 的值为( )
A、 B、 C、 D、2. 如图,已知直线AB∥CD∥EF , BD=2,DF=4,则 的值为( ) A、 B、 C、 D、13. 如图:在△ABC中,点D在BC边上,连接AD , 点G在线段AD上,GE BD , 且交AB于点E , GF AC , 且交CD于点F , 则下列结论一定正确的是( )
A、 B、 C、 D、13. 如图:在△ABC中,点D在BC边上,连接AD , 点G在线段AD上,GE BD , 且交AB于点E , GF AC , 且交CD于点F , 则下列结论一定正确的是( )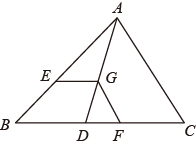 A、 B、 C、 D、4. 如图,四边形ABCD是平行四边形,点E在CD边上,则下列结论错误的是( )
A、 B、 C、 D、4. 如图,四边形ABCD是平行四边形,点E在CD边上,则下列结论错误的是( ) A、 B、 C、 D、5. 如图,点D,E分别在△ABC的边AB,AC上,DE的延长线交BC的延长线于点F,DG∥BC交AC于点G,则下列式子一定正确的是( )
A、 B、 C、 D、5. 如图,点D,E分别在△ABC的边AB,AC上,DE的延长线交BC的延长线于点F,DG∥BC交AC于点G,则下列式子一定正确的是( )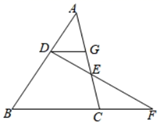 A、 B、 C、 D、6. 如图, , , 分别交 于点G,H,则下列结论中错误的是( )
A、 B、 C、 D、6. 如图, , , 分别交 于点G,H,则下列结论中错误的是( )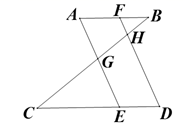 A、 B、 C、 D、7. 如图,在 ABC中,点D在AB边上,点E在BC边上,过点D作DG BC , 交AC于点G , 过点E作EH AB , 交AC于点H , DG的延长线与EH的延长线交于点F , 则下列式子一定正确的是( )
A、 B、 C、 D、7. 如图,在 ABC中,点D在AB边上,点E在BC边上,过点D作DG BC , 交AC于点G , 过点E作EH AB , 交AC于点H , DG的延长线与EH的延长线交于点F , 则下列式子一定正确的是( )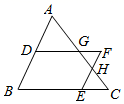 A、 B、 C、 D、8. 如图, 中, , 是中线, 是 上一点,作射线 ,交 于点 ,若 ,则 ( )
A、 B、 C、 D、8. 如图, 中, , 是中线, 是 上一点,作射线 ,交 于点 ,若 ,则 ( ) A、2 B、2.5 C、3 D、3.59. 如图,已知点D、E、F分别在 的边 、 、 上,连接 、 、 , , ,则下列结论错误的是( )
A、2 B、2.5 C、3 D、3.59. 如图,已知点D、E、F分别在 的边 、 、 上,连接 、 、 , , ,则下列结论错误的是( ) A、 B、 C、 D、10. 如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )
A、 B、 C、 D、10. 如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )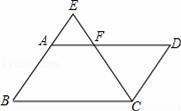 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在△ABC中,DE AB,CD:DA=2:3,DE=4,则AB的长为 .
 12. 如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于.
12. 如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于. 13. 如图, 与 的边 , 分别相交于 , 两点,且 .若 , ,则 等于.
13. 如图, 与 的边 , 分别相交于 , 两点,且 .若 , ,则 等于. 14. 如图,已知 , , ,那么 的长为 .
14. 如图,已知 , , ,那么 的长为 . 15. 如图5,已知直线l1∥l2∥l3 , 直线m与直线l1 , l2 , l3分别交于A,D,F:直线n与直线l1 , l2 , l3分别交于B,C,E。若 ,则 =。
15. 如图5,已知直线l1∥l2∥l3 , 直线m与直线l1 , l2 , l3分别交于A,D,F:直线n与直线l1 , l2 , l3分别交于B,C,E。若 ,则 =。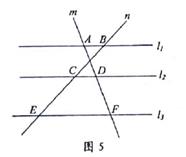 16. 如图,在 中, 是 边上的一点, 为 的中点,联结 并延长交 于点 ,则
16. 如图,在 中, 是 边上的一点, 为 的中点,联结 并延长交 于点 ,则
三、解答题
-
17. 如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
 18. 如图四边形CDEF是Rt△ACB的内接正方形,AC=4,BC=6,求ED的长.
18. 如图四边形CDEF是Rt△ACB的内接正方形,AC=4,BC=6,求ED的长. 19. 如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF.
19. 如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF.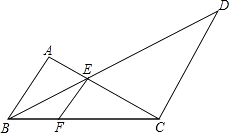 20. 如图.在△ABC中,E是AB的中点,D是AC上的一点,且AD:DC=2:3,BD与CE交于F,S△ABC=40,求SAEFD .
20. 如图.在△ABC中,E是AB的中点,D是AC上的一点,且AD:DC=2:3,BD与CE交于F,S△ABC=40,求SAEFD . 21. 如图.在△ABC中,E是AB的中点,D是AC上的一点,且AD:DC=2:3,BD与CE交于F,S△ABC=40,求SAEFD .
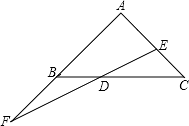
21. 如图.在△ABC中,E是AB的中点,D是AC上的一点,且AD:DC=2:3,BD与CE交于F,S△ABC=40,求SAEFD . 22. 一条直线与三角形ABC的三边BC,CA,AB(或其延长线)分别交于D,E,F如图所示).
22. 一条直线与三角形ABC的三边BC,CA,AB(或其延长线)分别交于D,E,F如图所示).求证: .
四、综合题
-
23. 如图,在△ABC中,DE∥AC,DF∥AE,BD:DA=3:2,BF=6,DF=8,
 (1)、求EF的长;(2)、求EA的长.24. 如图,已知AB∥CD,AD、BC 交于点E.
(1)、求EF的长;(2)、求EA的长.24. 如图,已知AB∥CD,AD、BC 交于点E. (1)、写出所有比值等于 的两条线段之比.(2)、若AE=3,DE=6,BC=12,求CE的长.25. 如图,已知 ,它们依次交直线 、 于点 、 、 和 、 、 .若 , = .
(1)、写出所有比值等于 的两条线段之比.(2)、若AE=3,DE=6,BC=12,求CE的长.25. 如图,已知 ,它们依次交直线 、 于点 、 、 和 、 、 .若 , = .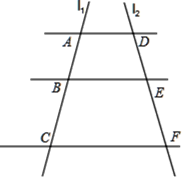 (1)、求 的长;(2)、如果 = , = ,求 的长.26. 在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度.在同一时刻的阳光下,他们合作完成了以下工作:
(1)、求 的长;(2)、如果 = , = ,求 的长.26. 在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度.在同一时刻的阳光下,他们合作完成了以下工作: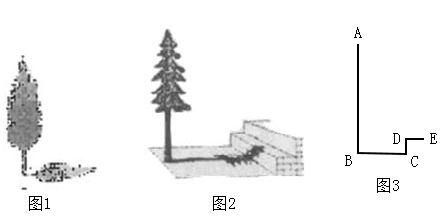
①测得一根长为l米的竹竿的影长为0.8米,甲树的影长为4.08米(如图l).
②测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为4.4米,一级台阶高为0.3米,落在第一级台阶的影子长为0.2米.
(1)、在横线上直接填写甲树的高度为米.(2)、图3为图2的示意图,请利用图3求出乙树的高度.27. 阅读下列材料,完成相应的任务:我们知道,利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢?如图,已知线段MN,用尺规在MN上求作点P,使 .
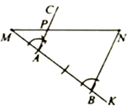
小颖的作法是:
①作射线MK(点K不在直线MN上);
②在射线MK上依次截取线段MA,AB,使 ,连接BN;
③作射线 ,交MN于点P点P即为所求作的点.
小颖作法的理由如下:
∵ (作法),∴
∵ (已知), (等量代换)
∵ (线段和差定义),∴ (等量代换,等式性质)
(1)、数学思考:
小颖作法理由中所缺的依据是:.(2)、拓展应用:
如图,已知线段a,b,c,求作线段d,使 a. B.
B.  C.
C. 