初中数学浙教版九年级上册第3章 圆的基本性质单元检测
试卷更新日期：2021-09-06 类型：单元试卷
一、单选题
-
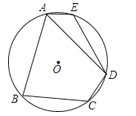
1. 如图，四边形 内接于 ， 为 的直径，点 为劣弧 的中点，若 ，则 的度数是（ ）
A、70° B、40° C、140° D、50°2. 如图，AB是⊙O的直径， ，∠COD=34°，则∠AOE的度数是（ ）
A、51° B、56° C、68° D、78°3. 已知 中， ， ， ，点P为边AB的中点，以点C为圆心，长度r为半径画圆，使得点A，P在⊙C内，点B在⊙C外，则半径r的取值范围是（ ）A、 B、 C、 D、4. 如图，四边形ABCD内接于⊙O，E在BC延长线上，若∠DCE＝50°，则∠A等于（ ）
A、40° B、50° C、70° D、80°5. 若扇形面积为36 ，圆心角为120°，则它的弧长为（ ）A、 B、 C、 D、6. 如图，Rt△ABC中，∠C＝90°，BC＝3，AC＝4，将△ABC绕点A顺时针旋转60°得到△AED ， 连接BE ， 则BE的长为（ ）
A、5 B、4 C、3 D、27. 如图，一条公路的转弯处是一段圆弧，点 是这段弧所在圆的圆心， ，点 是 的中点，点D是AB的中点，且 ，则这段弯路所在圆的半径为（ ）
A、 B、 C、 D、8. 如图， 是圆O的直径，C，D是弧 上的两点，连接 ， 相交于点E，若 ，那么 的度数为（ ）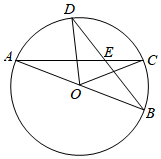
A、 B、 C、 D、9. 如图是由4个边长为a的正六边形组成的网格图，每个顶点均为格点，若该图中到点A的距离超过3的格点有且仅有6个，则a的取值范围为（ ）
A、 B、 C、 D、10. 《九章算术》第一章“方田”中讲述了扇形面积的计算方法：“今有宛田，下周三十步，径十六步，问为田几何？”大致意思为：现有一块扇形的田，弧长30步，其所在圆的直径是16步，则这块田面积为（ ）A、 平方步 B、 平方步 C、120平方步 D、240平方步二、填空题
-
11. 如图，⊙O是△ABC的外接圆，半径是2，∠BAC＝60°，则 的长是 ．
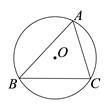12. 如图，正六边形ABCDEF内接于 ，若 ，则 的半径为.
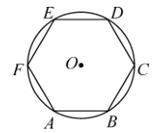13. 如图，四边形 内接于⊙ ， 为 的延长线上一点.若 °，则 的大小为.
14. 如图，在 中，半径 于点H ， 若 ，则 ．
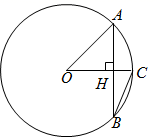15. 已知弦AB把圆周分成1：5的两部分，则弦AB所对的圆心角的度数为度。16. 如图，AB、AC都是圆O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N，如果MN= ，那么BC= ．
三、解答题
-
17. 如图，△ABC中，∠BAC=120o ， 以BC为边向外作等边△BCD，把△ABD绕着D点按顺时针方向旋转60o后到△ECD的位置。若AB=6，AC=4，求∠BAD的度数和AD的长.
18. 如图，AB为⊙O的直径，从圆上一点C作弦CD⊥AB，∠OCD的平分线交⊙O于P，求证： .
19.如图，在⊙O中，D、E分别是半径OA、OB的中点，C是⊙O上一点，CD=CE．
（1）求证：=；
（2）若∠AOB=120°，CD=2 ， 求半径OA的长．
20.如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在上．
（1）求∠E的度数；
（2）连接OD、OE，当∠DOE=90°时，AE恰好为⊙O的内接正n边形的一边，求n的值
21.将正六边形纸片按下列要求分割（每次分割纸片不得剩余）
第一次：将正六边形纸片分割成三个全等的菱形，然后选取其中一个菱形再分割成一个正六边形和两个全等的正三角形．（后面就依次用剩下的正六边形按上述方法分割…）
（1）请画出第一次分割示意图；
（2）若原正六边形的面积为a，请你将第一次，第二次，第三次分割后所得的正六边形的面积填入下表：
（3）猜想：分割后所得的正六边形的面积S与分割次数n有何关系？（S用含a和n的代数式表示）
22.如图，风车的支杆OE垂直于桌面，风车中心O到桌面的距离OE为25cm，小小风车在风吹动下绕着中心O不停地转动，转动过程中，叶片端点A、B、C、D在同一圆O上，已知⊙O的半径为10cm．
（1）风车在转动过程中，当∠AOE=45°时，求点A到桌面的距离（结果保留根号）．
（2）在风车转动一周的过程中，求点A相对于桌面的高度不超过20cm所经过的路径长（结果保留π）．
四、综合题
-
23. 阅读下列材料，并完成相应的学习任务：
我们知道三角形外接圆的圆心叫做三角形的外心，三角形内切圆的圆心叫做三角形的内心．由于三角形的三条高（或高所在的直线）相交于一点，因此我们把三角形三条高的交点叫做三角形的垂心．下面我们以锐角三角形为例，证明三角形的三条高相交于一点．
如图，在△ABC中，AD ， BE分别是BC ， AC边上的高，且AD与BE相交于点P ． 连接CP并延长，交AB于点F ．
求证：CF⊥AB ．
证明：分别过点A ， B ， C作它们所对边的平行线，三条平行线两两相交于点M ， N ， Q ． 分别连接PM ， PN ， PQ ．
∵MN BC ， MQ AB ， NQ AC ，
∴四边形MABC ， 四边形ANBC ， 四边形ABQC都是平行四边形．
∴BC=AM=AN ， AC=BN=BQ ， AB=MC=CQ ．
∵AD⊥BC ，
∴∠MAD=∠ADB=90°，即AD⊥MN ．
∴PM=PN ．
…
学习任务：
(1)、请将上面剩余的证明过程补充完整；(2)、点P是△MNQ的 ． （填出字母代号即可）A、内心 B、外心 C、垂心 D、重心(3)、若∠CAB=40°，则∠MPN=°．
24. 如图，在△ABC中，AB＝AC＝2 ，∠BAC＝120°，点D在AB上，AD＝2，以点A为圆心，AD长为半径的弧交AC于点E ， 与BC交于点F ， G ， P是 上一点．将AP绕点A逆时针旋转120°，得到AQ ， 连接CQ ， AF ．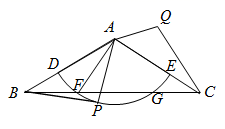
(1)、若BP与 所在圆相切，判断CQ与 所在圆的位置关系．并加以证明；(2)、求BF的长及扇形EAF的面积；(3)、若∠PAB＝m°，当∠ACQ＝30°，直接写出m的值．