初中数学浙教版九年级上册3.8 弧长及扇形的面积同步练习

试卷更新日期：2021-09-06 类型：同步测试

进入出卷网下载

一、单选题

1. 半径为 $2cm$ ，圆心角为 $90 °$ 的扇形的面积等于（）

A、 ${1cm}^{2}$ B、 ${πcm}^{2}$ C、 ${2πcm}^{2}$ D、 ${4πcm}^{2}$

查看试题解析
2. 一个扇形的半径为3cm，面积为 $π {cm}^{2}$ ，则此扇形的圆心角为（）

A、 $30 °$ B、 $40 °$ C、 $80 °$ D、 $120 °$

查看试题解析
3. 一条弧所对的圆心角为135°，弧长等于半径为3cm的圆的周长的5倍，则这条弧的半径为（）

A、45cm B、40cm C、35cm D、30cm

查看试题解析
4. 一根钢管放在V形架内，其横截面如图所示，钢管的半径是24cm，若 $∠ A C B = 60 °$ ，则劣弧AB的长是（）

A、 $8 πcm$ B、 $16 πcm$ C、 $32 πcm$ D、 $192 πcm$

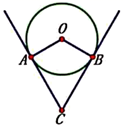查看试题解析
5. 如图，在4×4的正方形网格中，若将 $△ A B C$ 绕着点A逆时针旋转得到 $△ A B^{'} C^{'}$ ，则 $\overset{⌢}{B B^{'}}$ 的长为（）

A、 $π$ B、 $\frac{π}{2}$ C、 $7 π$ D、 $6 π$

查看试题解析
6. 如图，在 $Rt △ A B C$ 中， $∠ A B C = 40 °$ ， $A B = 6$ ，斜边 $A B$ 是半圆 $O$ 的直径，点 $D$ 是半圆上的一个动点，连接 $C D$ 与 $A B$ 交于点 $E$ ，若 $△ B C E$ 是等腰三角形，则弧 $B D$ 的长为（）

A、 $\frac{4}{3} π$ B、 $\frac{2}{3} π$ 或 $\frac{7}{3} π$ C、 $\frac{4}{3} π$ 或 $\frac{7}{3} π$ D、 $\frac{2}{3} π$ 或 $\frac{7}{6} π$

查看试题解析
7. 如图， $A B$ 是 $⊙ O$ 的直径， $C D$ 是弦， $C D ∕ ∕ A B ， ∠ B C D = 30 ° ， A B = 6$ ，则 $\overset{⌢}{A C}$ 的长为（　　）

A、 $π$ B、 $4 π$ C、 $2 π$ D、 $45 π$

查看试题解析
8. 如图，正六边形ABCDEF内接于⊙O ，边长AB＝2，则扇形AOB的面积为（　　）

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、π D、 $\frac{4 π}{3}$

查看试题解析
9. 某扇形的圆心角为 $150 °$ ，其弧长为 $20 π cm$ ，则此扇形的面积是（）

A、 $120 π cm$ B、 $480 π {cm}^{2}$ C、 $240 π {cm}^{2}$ D、 $240 {cm}^{2}$

查看试题解析
10. 如图，点A ， B ， C在 $⊙ O$ 上，四边形 $O A B C$ 是平行四边形．若对角线 $A C = 2 \sqrt{3}$ ，则 $\overset{⌢}{A C}$ 的长为（）

A、 $\frac{3 π}{2}$ B、 $\frac{5 π}{3}$ C、 $\frac{4 π}{3}$ D、 $\frac{4 \sqrt{3} π}{3}$

查看试题解析

二、填空题

11. 如图，已知扇形的圆心角为 $150 °$ ，半径为1，那么该扇形的弧长为．（结果保留 $π$ ）

查看试题解析
12. 如图所示的网格中，每个小正方形的边长均为 $1$ ，点 $A$ ， $B$ ， $D$ 均在小正方形的顶点上，且点 $B$ ， $C$ 在 $\overset{⌢}{A D}$ 上， $∠ B A C = 22.5 °$ ，则 $\overset{⌢}{B C}$ 的长为.

查看试题解析
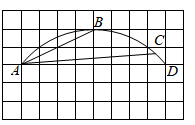13. 某扇形的圆心角为 $45 °$ ，面积为 $9 π$ ，该扇形的弧长为．

查看试题解析
14. 如图，扇形纸扇完全打开后，外侧两竹条AB，AC夹角为120°，扇面BD的长为20cm，扇面(阴影部分)的面积为 $\frac{800 π}{3}$ cm² ，则竹条AB的长为cm。

查看试题解析
15. 如图， $△ A B C$ 是边长为6的等边三角形，分别以点 $A$ 、 $B$ 、 $C$ 为圆心，以2为半径画弧，则图中阴影部分图形的周长为．（结果保留 $π$ ）

查看试题解析
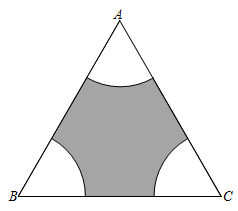16. CD是以AB为直径的⊙O的一条弦，CD $//$ AB ， ∠CAD＝40°，若⊙O的半径为9cm ，则阴影部分的面积为cm² ．

查看试题解析

三、解答题

17. 如图所示，已知甲、乙、丙三种图案的地砖，它们都是边长为4的正方形．

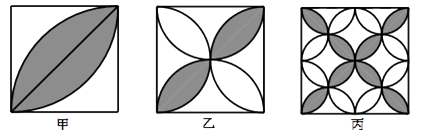
①甲地砖以正方形的边长为半径作弧得到甲图所示的阴影部分；
②乙地砖以正方形的边长为直径作弧得到乙图所示的阴影部分；
③丙地砖以正方形边长的一半为直径作弧得到丙图所示的阴影部分；
设三种地砖的阴影部分面积分别为S_甲、S_乙和S_丙．

(1)、求S_甲．（结果保留π）

(2)、请你直接将S_甲和S_乙的数量关系填在横线上：．

(3)、由题（2）中面积的数量关系，可直接求得S_丙＝．（结果保留π）

查看试题解析
18. 制造弯形管道时，经常要先按中心线计算“展直长度”，再备料．下图是一段管道，其中直管道部分AB的长为3 000mm，弯形管道部分BC，CD弧的半径都是1 000mm，∠O=∠O’=90°，计算图中中心虚线的长度．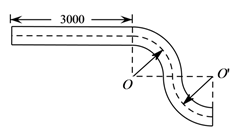

查看试题解析
19. 如图，五个半径为2的圆，圆心分别是点A，B，C，D，E，则图中阴影部分的面积和是多少？

查看试题解析
20.
如图，⊙O的直径EF为10cm，弦AB、CD分别为6cm、8cm，且AB∥EF∥CD．求图中阴影部分面积之和．

查看试题解析
21.
如图，点A、B、C、D、E都在⊙O上，AC平分∠BAD，且AB∥CE，求证：AD=CE．

查看试题解析
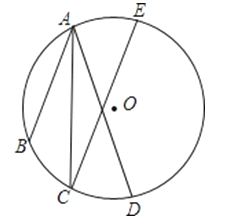22.
如图，王虎使一长为4cm，宽为3cm的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A位置变化为A→A₁→A₂ ，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为多少？

查看试题解析

四、综合题

23. 某灯具厂生产一批台灯罩，如图的阴影部分为灯罩的侧面展开图.已知半径 $O A = 24 cm$ ， $O C = 12 cm$ ， $∠ A O B = 135 °$ .（计算结果保留 $π$ ）

(1)、若要在灯罩的上下边缘镶上花边（花边的宽度忽略不计），至少需要多长的花边？

(2)、求灯罩的侧面积（接缝处忽略不计）.

查看试题解析
24. 如图，在Rt△ABC中，∠C=90°，AC=BC，点O在AB上，以O为圆心，OA为半径作⊙O，与BC相切于点D，且交AB于点E。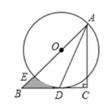

(1)、连结AD，求证：AD平分∠CAB；

(2)、若BE= $\sqrt{2}$ -1，求阴影部分的面积。

查看试题解析
25. 如图，在正方形网格中，每个小正方形的边长都为1

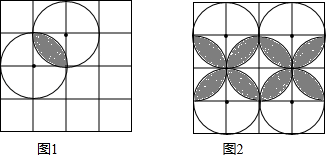(1)、如图1，两个半径为1的圆相交，则阴影部分的面积为；

(2)、图2是以（1）中的图形为基本图形，通过一组图形变换得到的，这组变换可以是.（写出一组即可）（填入序号）.①轴对称变换；②平移变换；③旋转变换.

查看试题解析
26. 如图，C，D是以AB为直径的半圆周的三等分点，CD＝8cm，P是直径AB上的任意一点.

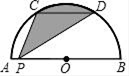(1)、求 $\overset{⌢}{C D}$ 的长；

(2)、求阴影部分的面积.

查看试题解析
27. 如图，有一直径MN=4的半圆形纸片，其圆心为点P，从初始位置Ⅰ开始，在无滑动的情况下沿数轴向右翻滚至位置Ⅳ，其中位置Ⅰ中的MN平行于数轴，且半⊙P与数轴相切于原点O；位置Ⅱ和位置Ⅳ中的MN垂直于数轴；位置Ⅲ中的MN在数轴上.
解答下列问题：

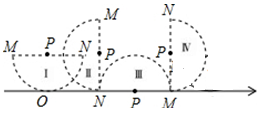(1)、位置Ⅰ中的MN与数轴之间的距离为；

(2)、位置Ⅱ中的半⊙P与数轴的位置关系是；

(3)、求位置Ⅲ中的圆心P在数轴上表示的数；

(4)、纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时，求该纸片所扫过图形的面积.

查看试题解析
28. 如图，已知AB为⊙O的直径，BD和CD为⊙O的切线，切点分别为B和C．

(1)、求证：AC∥OD；

(2)、当BC=BD，且BD=6cm时，求图中阴影部分的面积（结果不取近似值）．

查看试题解析
29. 如图，点 $D$ 在⊙ $O$ 的直径 $A B$ 的延长线上，点 $C$ 在⊙ $O$ 上， $A C = C D$ ， $∠ A C D = 120 °$ ．

(1)、求证： $C D$ 是⊙ $O$ 的切线；

(2)、若⊙ $O$ 的半径为 $2$ ，求图中阴影部分的面积．

查看试题解析