浙江省宁波市余姚市2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-09-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个数中比﹣5小的数是（）

A、1 B、0 C、﹣4 D、﹣6

查看试题解析
2. 下列式子中，正确的是（）

A、 $| - 5 | = - 5$ B、 $- | - 5 | = 5$ C、 $- (- 5) = 5$ D、 $- (- 5) = - 5$

查看试题解析
3. 下列两个数是互为相反数的是（）

A、 $\sqrt{{(- 2)}^{2}}$ 与 $\sqrt[3]{- 8}$ B、 $| - \sqrt{2} |$ 与 $\sqrt{2}$ C、 $\sqrt[3]{- 8}$ 与 $- \sqrt[3]{8}$ D、 $- 2 与 - \frac{1}{2}$

查看试题解析
4. 下列说法正确的是（　　）

A、带有根号的数是无理数 B、无限小数是无理数 C、无理数是无限不循环小数 D、无理数是开方开不尽的数

查看试题解析
5. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划“一带一路”地区覆盖总人口44亿，这个数用科学记数法表示为（）

A、44×10⁸ B、4.4×10⁹ C、4.4×10⁸ D、4.4×10¹⁰

查看试题解析
6. 设a为正整数，且a＜ $\sqrt{37}$ ＜a+1，则a的值为（）

A、5 B、6 C、7 D、8

查看试题解析
7. 数轴上到数-2所表示的点的距离为4的点所表示的数是（）

A、-6 B、6 C、2 D、-6或2

查看试题解析
8. 把方程 $\frac{2 x - 1}{4} = 1 - \frac{3 - x}{8}$ 去分母后，正确的结果是 $（$ $）$

A、2x-1=1-（3-x） B、2（2x-1）=1-（3-x） C、2（2x-1）=8-3+x D、2（2x-1）=8-3-x

查看试题解析
9. 一支钢笔正好与一把直尺平靠放在一起（如图），小明发现：钢笔的笔尖端（ $A$ 点）正好对着直尺刻度约为 $5.6 cm$ 处，另一端（ $B$ 点）正好对着直尺刻度约为 $20.6 cm$ .钢笔的中点位置的刻度约为（）

A、 $15cm$ B、 $7 .5cm$ C、 $13 .1cm$ D、 $12 .1cm$

查看试题解析
10. 将四张边长各不相同的正方形纸片按如图方式放入矩形 $A B C D$ 内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为 $l$ .若知道 $l$ 的值，则不需测量就能知道周长的正方形的标号为（）

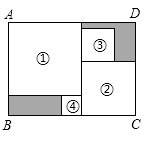A、① B、② C、③ D、④

查看试题解析

二、填空题

11. 实数8的立方根是．

查看试题解析
12. 已知a=3，则代数式 $a (a + 1)$ 的值是.

查看试题解析
13. 若单项式 $2 x^{m} y^{3}$ 与 $3 x y^{m + n}$ 是同类项，则 $\sqrt{2 m + n}$ 的值是.

查看试题解析
14. 已知方程 $(m - 2) x^{| m | - 1} + 7 = 0$ 是关于 $x$ 的一元一次方程，则 $m =$ .

查看试题解析
15. 八年级某班组织垃圾分类知识宣传活动，全班学生分成甲乙两队，甲队收集垃圾分类知识资料，乙队收集废物利用资料，甲队人数是乙队人数的2倍，活动过程中需要从甲队中调8人去乙队后，甲队人数为乙队人数的一半还多9人，求本班总人数；设乙队有x人，可列方程：.

查看试题解析
16. 下面每个正方形中的五个数之间都有相同的规律，根据这种规律，则第4个正方形中间数字m为，第n个正方形的中间数字为.（用含n的代数式表示）
…… ……

查看试题解析

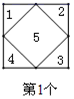
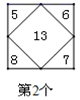
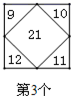
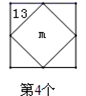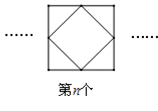三、解答题

17. 计算：

(1)、6-（-5）+（-11）

(2)、 $16 \div {(- 2)}^{3} - (- \frac{1}{8}) \times (- 4)$

(3)、（−2）²+| $\sqrt{2} - 1$ |- $\sqrt[3]{27}$

查看试题解析
18. 解方程：

(1)、 $3 x + 1 = - 5$

(2)、 $\frac{2 x - 1}{3} = \frac{x + 1}{4} - 1$

查看试题解析
19. 先化简，再求值：2x³－(7x²－9x)－2(x³－3x²＋4x)，其中x＝－1.

查看试题解析
20. 如图，已知直线 $l$ 和直线外三点 $A ， B ， C$ ，按下列要求画图，填空：

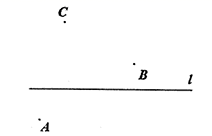
（ 1 ）画射线 $A B$ ；

（ 2 ）连接 $B C$ ；

（ 3 ）延长 $C B$ 至 $D$ ，使得 $B D = B C$ ；

（ 4 ）在直线 $l$ 上确定点 $E$ ，使得 $A E + C E$ 最小，请写出你作图的依据 .

查看试题解析
21. 一位病人早晨8时的体温是39.7℃，下表是该病人一天中的体温变化．
时间
11时
14时
17时
20时
23时
2时（次日）
5时
8时
体温变化（℃）
-1.5
+1
+0.2
-1.2
-0.5
-0.5
-0.2
+0.2

(1)、这位病人的体温最低是多少摄氏度？

(2)、若正常体温是37℃，那么从体温看，这位病人的病情是在恶化还是在好转？

查看试题解析
22. 如图，一个大长方形场地割出如图所示的“L”型阴影部分，请根据图中所给的数据，回答下列问题：

(1)、用含x，y的代数式表示阴影部分的周长并化简.

(2)、若x＝4米，y＝3米时，要给阴影部分场地围上价格每米8元的围栏作功能区，请计算围栏的造价.

查看试题解析
23. 某市对居民生活用电实行“阶梯电价”收费，具体收费标准见下表：

一户居民一个月用电量的范围

电费价格（单位：元/度）

不超过150度

a

超过150度的部分

b

今年5月份，该市居民甲用电100度，交电费80元；居民乙用电200度，交电费170元.

(1)、上表中，a＝， b＝；

(2)、若该市某居民7月用量250度电，则该居民需交多少电费？

(3)、若该市某居民8月份交的电费的平均电价为0.9元/度，则该居民8月份用电多少度？

查看试题解析
24. 如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”.图中点A表示－11，点B表示10，点C表示18，我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速.设运动的时间为t秒.问：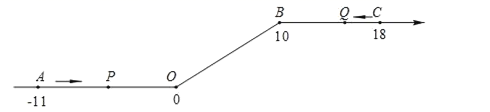

(1)、t为6秒时，P、Q点所在位置对应点的数分别是多少?

(2)、动点P从点A运动至C点需要多少时间？

(3)、P、Q两点相遇时，求出相遇点M所对应的数是多少；

(4)、求当t为何值时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.

查看试题解析

时间	11时	14时	17时	20时	23时	2时（次日）	5时	8时
体温变化（℃）	-1.5	+1	+0.2	-1.2	-0.5	-0.5	-0.2	+0.2

一户居民一个月用电量的范围	电费价格（单位：元/度）
不超过150度	a
超过150度的部分	b