浙教版数学九上3.7 正多边形同步练习

试卷更新日期：2021-09-06 类型：同步测试

进入出卷网下载

一、单选题

1. 已知正六角形的边心距为 $\sqrt{3}$ ，则它的周长是（）

A、6 B、12 C、6 $\sqrt{3}$ D、12 $\sqrt{3}$

查看试题解析
2. 古希腊数学家欧几里得在《几何原本》中记载了用尺规作某种六边形的方法，其步骤是：①在⊙O上任取一点A ，连接AO并延长交⊙O于点B ， BO为半径作圆孤分别交⊙O于C ， D两点，DO并延长分交⊙O于点E ， F；④顺次连接BC ， FA ， AE ， DB ，得到六边形AFCBDE ．连接AD ，交于点G ，则下列结论错误的是．

A、△AOE的内心与外心都是点G B、∠FGA＝∠FOA C、点G是线段EF的三等分点 D、EF＝ $\sqrt{2}$ AF

查看试题解析
3. 若⊙O的内接正n边形的边长与⊙O的半径相等，则n的值为（）

A、4 B、5 C、6 D、7

查看试题解析
4. 正多边形的内切圆与外接圆的半径之比为 $\frac{\sqrt{2}}{2}$ ，则这个正多边形为（）

A、正十二边形 B、正六边形 C、正四边形 D、正三角形

查看试题解析
5. 圆内接正六边形的边长与该边所对的劣弧的长的比是（）

A、1: $\sqrt{2}$ B、1:π C、3:π D、6:π

查看试题解析
6. 如图A，B，C是 $⊙ O$ 上顺次3点，若 $A C$ ， $A B$ ， $B C$ 分别是 $⊙ O$ 内接正三角形、正方形、正n边形的一边，则 $n =$ （）

A、9 B、10 C、12 D、15

查看试题解析
7. 如图，以正五边形 $A B C D E$ 的对角线 $B E$ 为边，作正方形 $B E F G ，$ 使点 $A$ 落在正方形 $B E F G$ 内，则 $∠ A B G$ 的度数为（）

A、 $18^{\circ}$ B、 $36^{\circ}$ C、 $54^{\circ}$ D、 $72^{\circ}$

查看试题解析
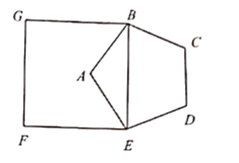8. 在圆内接正方形ABCD中，正方形的边长AB是8，则这个正方形的中心角和边心距是（）

A、90°，4 B、90°，1 C、45°，4 D、45°，1

查看试题解析
9. 我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出，“周三径一”不是圆周率值，实际上是圆内接正六边形周长和直径的比值(图1)。刘徽发现，圆内接正多边形边数无限增加时，多边形的周长就无限逼近圆周长，从而创立“割圆术”，为计算圆周率建立起相当严密的理论和完善的算法。如图2，六边形ABCDEF是圆内接正六边形，把每段弧二等分，作出一个圆内接正十二边形，连结AG，CF，AG交CF于点P，若AP=2 $\sqrt{6}$ ，则 $\overset{⌢}{C G}$ 的长为（）

A、 $\frac{π}{2}$ B、 $\frac{3}{4}$ π C、 $\frac{\sqrt{3}}{3}$ π D、 $\frac{2}{3}$ π

查看试题解析
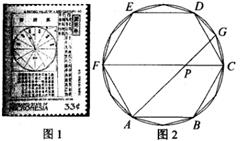10. 如图，有一个边长为2cm 的正六边形纸片，若在该纸片上剪一个最大圆形，则这个圆形纸片的直径是（） .

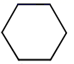A、 $\sqrt{3}$ cm B、2 $\sqrt{3}$ cm C、2cm D、4cm

查看试题解析

二、填空题

11. 边长为 $4cm$ 的正六边形，它的外接圆与内切圆半径的比值是．

查看试题解析
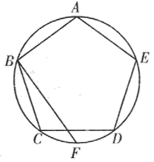12. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，F是 $\overset{⌢}{C D}$ 的中点，则 $∠ C B F$ 的度数为.

查看试题解析
13. 如图，⊙O的半径为1，作两条互相垂直的直径AB、CD，弦AC是⊙O的内接正四边形的一条边.若以A为圆心，以1为半径画弧，交⊙O于点E，F，连接AE、CE，弦EC是该圆内接正n边形的一边，则该正n边形的面积为.

查看试题解析
14. 如图，在边长为 $2 c m$ 的正六边形 $A B C D E F$ 中，点P在BC上，则 $△ P E F$ 的面积为.

查看试题解析
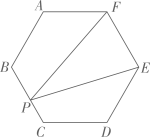15. 如图，在正十边形A₁A₂A₃A₄A₅A₆A₇A₈A₉A₁₀中，连接A₁A₄、A₁A₇ ，则∠A₄A₁A₇＝°.

查看试题解析
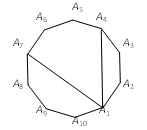16. 如图，有一个圆O和两个正六边形T₁ ， T₂ ． T₁的6个顶点都在圆周上，T₂的6条边都和圆O相切(我们称T₁ ， T₂分别为圆O的内接正六边形和外切正六边形)．若设T₁ ， T₂的边长分别为a，b，圆O的半径为r，则r：a=；r：b=；正六边形T₁ ， T₂的面积比S₁：S₂的值是．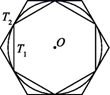

查看试题解析

三、解答题

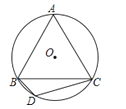
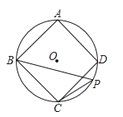
17.
如图，已知等边△ABC内接于⊙O，BD为内接正十二边形的一边，CD=5 $\sqrt{2}$ cm，求⊙O的半径R．

查看试题解析
18.
如图，正方形ABCD的外接圆为⊙O，点P在劣弧 $\overset{\land}{C D}$ 上（不与C点重合）．
（1）求∠BPC的度数；
（2）若⊙O的半径为8，求正方形ABCD的边长．

查看试题解析
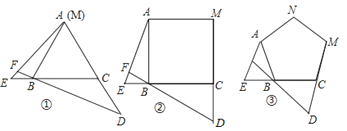
19.
如图③，点E，D分别是正三角形ABC，正四边形ABCM，正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点，且△ABE与△BCD能相互重合，DB的延长线交AE于点F．
（1）在图①中，求∠AFB的度数；
（2）在图②中，∠AFB的度数为，图③中，∠AFB的度数为；
（3）继续探索，可将本题推广到一般的正n边形情况，用含n的式子表示∠AFB的度数．

查看试题解析
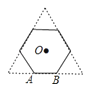
20.
如图，正三角形的边长为6cm，剪去三个角后成一个正六边形．
①求这个正六边形的边长．
②求这个正六边形的边心距．
③设这个正六边形的中心为O，一边为AB，则AB绕点O旋转一周所得的图形是怎样的？（作图表示出来）并求出这条线段AB划过的面积．

查看试题解析
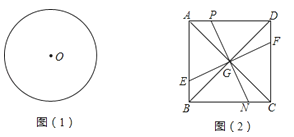
21.
问题探究
（1）请在图（1）中作出两条直线，使它们将圆面积四等分，并写出作图过程；
拓展应用
（2）如图（2），M是正方形ABCD内一定点，G是对角线AC、BD的交点．连接GM并延长，分别交AD、BC于P、N．过G做直线EF⊥GM，分别交AB、CD于E、F．求证：PN、EF将正方形ABCD的面积四等分．

查看试题解析
22.
如图，圆心角120°的扇形OMN，绕着正六边形ABCDEF的中心O旋转，OM交AB于H，ON交CD于K，OM＞OA．
（1）证明：△AOH≌△COK；
（2）若AB=2，求正六边形ABCDEF与扇形OMN重叠部分的面积．

查看试题解析
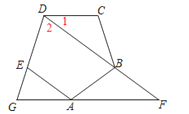
23.
如图，已知正五边形ABCDE，AF∥CD交DB的延长线于点F，交DE的延长线于点G．
（1）写出图中所有的等腰三角形；
（2）求证：∠G=2∠F．

查看试题解析

四、综合题

24. 图1是某景区的纪念币，一面有一个正十边形，示意图如图2所示，其外接圆的圆心为O，直径为 $20 mm$ .

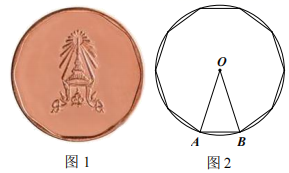(1)、求这个正十边形的边长 $A B$ .

(2)、求这个正十边形的面积.（参考数据： $\sin 18 ° \approx 0.31 ， \cos 18 ° \approx 0.95 ， \tan 18 ° \approx 0.32$ ）

查看试题解析
25. 如图，正五边形ABCD中，点F、G分别是BC、CD的中点，AF与BG相交于H．

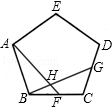(1)、求证：△ABF≌△BCG；

(2)、求∠AHG的度数．

查看试题解析
26. 如图，有一个圆O和两个正六边形T₁ ， T₂ ． T₁的6个顶点都在圆周上，T₂的6条边都和圆O相切（我们称T₁ ， T₂分别为圆O的内接正六边形和外切正六边形）．

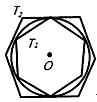(1)、设T₁ ， T₂的边长分别为a，b，圆O的半径为r，求r：a及r：b的值；

(2)、求正六边形T₁ ， T₂的面积比S₁：S₂的值．

查看试题解析
27. 已知某种月饼形状的俯视图如图1所示，该形状由1个正六边形和6个半圆组成，半圆直径与正六边形的边长相等.

现商家设计了2种棱柱体包装盒，其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率= $\frac{月饼面积}{包装盒底面面积}$ ×100%)

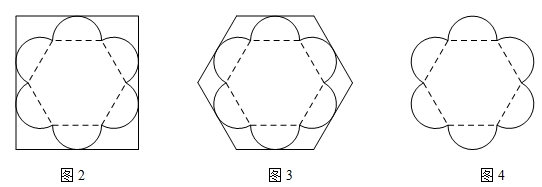(1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%)；

(2)、考虑到节约成本，商家希望底面利用率能够不低于80%，且底面图形仍然采用最基本的几何形状，请问商家的要求是否能够满足，若可以满足，请设计一种方案，并直接写出此时的利用率；若不能满足，请说明理由.

查看试题解析