广西壮族自治区百色市德保县2020-2021学年七年级上学期数学期中考试试卷
试卷更新日期:2021-09-06 类型:期中考试
一、单选题
-
1. ﹣3的相反数为( )A、﹣3 B、﹣ C、 D、32. 如果水位下降5m记作-5m,那么水位上升2m记作 ( )A、+2m B、-2m C、+3m D、-3m3. 比较数的大小,下列结论错误的是( )A、-5<-3 B、 < < C、- <0< D、2>-3>04. 近似数0.580 0的精确度是( )A、精确到百分位 B、精确到十万分位 C、精确到万分位 D、精确到千分位5. 2019年1月3日,“嫦娥四号”探测器成功着陆在月球背面东经177.6度、南纬45.5度附近,实现了人类首次在月球背面软着陆.数字177.6用科学记数法表示为( )A、0.1776×103 B、1.776×102 C、1.776×103 D、17.76×1026. 数轴上表示-1和表示-7的两点之间的距离是( )A、6 B、-6 C、8 D、-87. 下列不是同类项的是 ( )A、 与 B、12与 C、 与 D、 与8. 下列运算中,正确的是( )A、 B、 C、 D、9. “双12”前,某微商店在京东以 元每个的价格购进充电宝50个,后又从天猫以 元每个的价格购进相同型号的充电宝30个 ,“双12”时以 元每个的价格在平台全部卖出,则该微商( )A、亏损了 B、盈利了 C、不亏不盈 D、亏损还是盈利由 , 的值决定10. 已知 , ,那么 的值为( )A、 B、 C、-1 D、11. 若单项式 与单项式 是同类项,则 与 的值分别是( )A、 , B、 , C、 , D、 ,12. 1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:取正整数5,最少经过下面5步运算可得1,即: ,如果正整数 最少经过6步运算可得到1,则 的值为( )A、 10 B、32 C、64 D、10或64
二、填空题
-
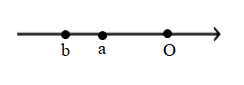
13. 计算: .14. 若 , ,则 的值为.15. 已知 , 两数在数轴上对应的点如图所示,则 (填“<”、“>”或“=”).
 16. 根据如图所示的程序计算,若输入的x的值为-2,则输出的y值为.
16. 根据如图所示的程序计算,若输入的x的值为-2,则输出的y值为.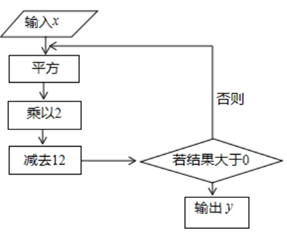 17. 一批上衣的进价为每件 元,在进价的基础上提高50%后作为零售价,由于季节原因,打6折促销,则打折后每件上衣的价格为元.18. 如图,用棋子摆出下列一组图形:
17. 一批上衣的进价为每件 元,在进价的基础上提高50%后作为零售价,由于季节原因,打6折促销,则打折后每件上衣的价格为元.18. 如图,用棋子摆出下列一组图形:
按照这种规律摆下去,第2020个图形用的棋子个数是.
三、解答题
-
19. 计算:20. 计算:21. 计算:22. 计算:23. 先化简,再求值 ,其中 .24. 随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50 km为标准,多于50 km的记为“+”,不足50 km的记为“-”,刚好50 km的记为“0”.
第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程(km)
-8
-11
-14
0
-16
+41
+8
(1)、请求出这七天平均每天行驶多少千米;(2)、若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?25. 阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用整体思想解决下列问题:(1)、把 看成一个整体,合并 .(2)、已知 ,求 的值;(3)、已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.26. 小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)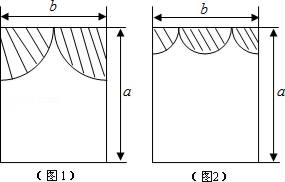 (1)、用代数式表示窗户能射进阳光的面积是.(结果保留π)(2)、当 ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)(3)、小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)
(1)、用代数式表示窗户能射进阳光的面积是.(结果保留π)(2)、当 ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)(3)、小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)