重庆主城区六校联盟2021届数学中考模拟试卷

试卷更新日期：2021-09-06 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的相反数为（）

A、﹣3 B、﹣ $\frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看试题解析
2. 计算m²•m³的结果是（）

A、m⁶ B、m⁵ C、m⁸ D、m⁹

查看试题解析
3. 要使分式 $\frac{1}{x - 2}$ 有意义，则x的取值范围是（）

A、x≠2 B、x≥﹣2 C、x≥2 D、x≠﹣2

查看试题解析
4. 中国载人航天工程办公室15日透露，神舟十二号载人航天飞船预计将于今年6月在酒泉卫星发射中心发射升空，神舟飞船是由专门为其研制的“长征二号”火箭发射升空，火箭的起飞质量为497000千克，数据497000用科学记数法可以表示为（）

A、497×10³ B、0.497×10⁶ C、4.97×10⁵ D、49.7×10⁴

查看试题解析
5. 估计 $\sqrt{2}$ × $\sqrt{14}$ 的值应在（）

A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间

查看试题解析
6. 如图，在△ABC外任取一点O，连接AO、BO、CO，并分别取它们的中点D、E、F，顺次连接DE、EF、DF得到△DEF，则下列说法错误的是（）

A、△DEF与△ABC是位似图形 B、△DEF与△ABC是相似图形 C、△DEF与△ABC的周长比是1：2 D、△DEF与△ABC的面积比是1：2

查看试题解析
7. 如图，△ABC的边AC与⊙O相交于C、D两点，且经过圆心O，边AB与⊙О相切，切点为B，如果∠A＝40°，那么∠C等于（）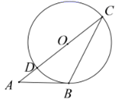

A、50° B、40° C、25° D、20°

查看试题解析
8. 《九章算术》中记载：“今有甲乙二人持钱不知其数.甲得乙半而钱五十，乙得甲太半而亦钱五十.问甲、乙持钱各几何？”其大意是：今有甲、乙两人各带了若干钱，如果甲得到乙所有钱的一半，那么甲共有钱50；如果乙得到甲所有钱的三分之二，那么乙也共有钱50，问甲、乙两人共带了多少钱？设甲带钱为x，乙带钱为y，根据题意，可列方程组为（）

A、 ${\begin{matrix} \frac{x}{2} + y = 50 \\ x + \frac{2 y}{3} = 50 \end{matrix}$ B、 ${\begin{matrix} x + \frac{y}{2} = 50 \\ \frac{2 x}{3} + y = 50 \end{matrix}$ C、 ${\begin{matrix} x + \frac{y}{2} = 50 \\ y + \frac{2}{3} (x + \frac{y}{2}) = 50 \end{matrix}$ D、 ${\begin{matrix} x = 50 + \frac{y}{2} \\ y = 50 + \frac{2 x}{3} \end{matrix}$

查看试题解析
9. 重庆朝天门码头位于置庆市油中半岛的嘉陵江与长江交汇处，是重庆最古老的码头.如图，小王在码头某点E处测得朝天门广场上的某高楼AB的顶端A的仰角为45°，接着他沿着坡度为1：2.4的斜坡EC走了26米到达坡顶C处，到C处后继续朝高楼AB的方向前行16米到D处，在D处测得A的仰角为74°，则此时小王距高楼的距离BD的为（）米（结果精确到1米，参考数据：sin74°≈0.96，cos74°≈0.28，tan74°≈3.49）

A、12 B、13 C、15 D、16

查看试题解析
10. 若关于x的一元一次不等式组 ${\begin{array}{l} 3 x + 1 \leq 2 (x - 2) \\ \frac{x - 2 a}{3} < 1 \end{array}$ 的解集为x≤－5，且关于x的分式方程 $\frac{2 + a x}{3 - x} + 2 = \frac{4}{x - 3}$ 有非负整数解，则符合条件的所有整数a的和为（）

A、－6 B、－4 C、－2 D、0

查看试题解析
11. 已知A、B、C三地顺次在同一直线上，甲、乙两人均骑车从A地出发，以同一路线向C地匀速行驶.甲比乙早出发5分钟，甲到达B地休息了2分钟后，乙追上了甲，接着，甲、乙同时从B地以各自的原速继续向C地行驶.当乙到达C地后，乙立即掉头并以原速的 $\frac{5}{4}$ 按原路返回A地；而甲也立即以原速的 $\frac{4}{3}$ 继续向C地行驶，到达C地就停止.若甲、乙之间的距离y（米）与甲出发的时间x（分）之间的函数关系如图所示，则下列说法错误的是（）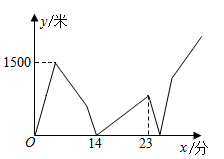

A、两地相距3600米 B、甲、乙两人在第24分钟时第二次相遇 C、甲从A地到C地共用时26分钟 D、当甲到达C地时，乙距B地2475米

查看试题解析
12. 如图，一次函数y＝﹣ $\frac{1}{2}$ x＋6与反比例函数y＝ $\frac{k}{x}$ （k＞0）交于A、B两点，过A、B两点分别作x轴、y轴的平行线交于点C，连接OC交AB于点D，连接OA.若△ADO的面积是△BDC面积的 $\frac{3}{2}$ 倍，则k的值是（）

A、8 B、10 C、10.5 D、12

查看试题解析

二、填空题

13. 计算： ${(π - 3)}^{0} + | - 1 | =$ .

查看试题解析
14. 已知： $\frac{a}{2} = \frac{b}{3}$ ，则 $\frac{3 a + b}{a - 2 b}$ ＝.

查看试题解析
15. 四张形状、大小完全相同的纸片上分别写有数字﹣1，0，2，4，现将写有数字的一面朝下并随机抽出两张纸片，则抽出的两张纸片上的数字之和为偶数的概率为.

查看试题解析
16. 如图，在正方形ABCD中，扇形BAD的半径AB＝4，以AB为直径的圆与正方形的对角线BD相交于O，连接AO.则图中阴影部分的面积为.（结果保留π）

查看试题解析
17. 如图，在△ABC中，∠ACB＝90°，AB＝8，BC＝6，D是AB的中点，将△BCD沿CD翻折至△ABC所在的平面内，得到△ECD，其中点B的对应点是点E，连接AE，则点E到直线AC的距离为.

查看试题解析
18. 新疆是我国最重要的棉花主产区，棉花的种植面积、总产量、单产量都位居世界首位.新疆的长绒棉品质暖和、透气、舒适，做衣服、被子都属于世界顶级，常年供不应求.长绒棉颜色对比分为白棉1级（记为A），白棉2级（记为B），白棉3级（记为C）.某厂家根据消费需求生产了甲、乙、丙三类被子，每床被子均由A、B、C三种棉花搭配而成，每床被子成本均为棉花成本之和.甲类被子每床由1千克A、0.5千克B、1千克C制成；乙类被子由0.5千克A、1千克B、2千克C制成.经核算，甲类被子每床成本是其A种棉花成本的2倍，且甲、乙、丙三类被子的利润率分别为30%、20%、25%，甲、丙两类被子每床售价之比为13：25，已知今年第一季度甲类被子的销售量是丙类被子的销售量的2倍，三类被子的总利润率正好与丙类被子的利润率相同，则乙类与丙类被子的销售量之比为.

查看试题解析

三、解答题

19. 计算：

(1)、（x＋2y）（x-2y）＋4y（x＋y）

(2)、（1 $- \frac{m}{m + 2}$ ）÷ $\frac{m^{2} - 4}{m^{2} + 4 m + 4}$

查看试题解析
20. 如图，在平行四边形ABCD中.

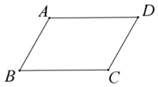(1)、尺规作图：作BC的垂直平分线EF，交BC于点E，交AD与点F；（不写作法，保留作图痕迹）

(2)、连接DE并延长交AB的延长线于点G，求证：AB＝BG.

查看试题解析

21. 今年春季开学后，为了庆祝伟大的中国共产党建党100周年，某校开展了“爱祖国•跟党走”的知识网上答题竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：

A.80≤x＜85，B.85≤x＜90，C.90≤x＜95，D.95≤x≤100）

下面给出了部分信息：

七年级10名学生的竞赛成绩是：90，81，90，86，99，95，96，100，89，84

八年级10名学生的竞赛成绩在C组中的数据是：90，94，94

七，八年级抽取的学生竞赛成绩统计表

年级	七年级	八年级
平均数	91	91
中位数	90	b
众数	c	100
方差	52	50.4

根据以上信息，解答下列问题：

(1)、直接写出上述图表中a、b、c的值；

(2)、根据以上数据，你认为该校七、八年级中哪个年级学生掌握的相关知识较好？请说明理由（一条理由即可）；

(3)、该校七、八年级各600人参加了此次网上答题竞赛活动，估计参加竞赛活动成绩优秀（x≥90）的学生人数是多少？

查看试题解析

22. 某枇杷园种植的枇杷除了运往市区销售外，还可以让市民亲自去生态农业园购买.已知今年4月份该枇杷在市区、园区的销售价格分别为10元/千克、8元/千克，4月份一共销售了3000千克，总销售额为26000元.

(1)、今年4月份该枇杷园在市区、园区销售枇杷各多少千克？

(2)、5月份是枇杷产出旺季.为了促销，生态农业园决定5月份将该枇杷在市区、园区的销售价格均在今年4月份的基础上降低 $\frac{1}{2}$ m%，预计这种枇杷在市区、园区的销售量将在今年4月份的基础上分别增长3m%、25%，要使5月份该枇杷的总销售额达到30000元，求m的值.

查看试题解析

23. 在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程.以下是我们研究函数

y = x | x + 2 | + a x^{2} + k

性质及其应用的部分过程，请按要求完成下列各小题.

x	…	﹣4	﹣3	﹣2	$- \frac{3}{2}$	﹣1	$- \frac{1}{2}$	0	$\frac{1}{2}$	1	…
y	…	7	5	3	$\frac{1}{2}$	﹣1	$- \frac{3}{2}$	﹣1	$\frac{1}{2}$	3	…

(1)、如表是y与x的几组对应值，则a＝， k＝；

(2)、如图，在平面直角坐标系中，已描出了部分点并绘制了部分图象，请把该函数的图象补充完整，并写出该函数的一条性质： ▲ ；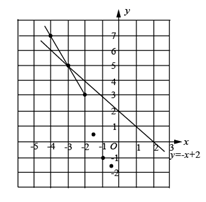

(3)、如图，在平面直角坐标系中作出了函数y＝﹣x＋2的图象，结合你所画的函数图象，直接写出不等式x|x＋2|＋ax²＋x﹣3≥0的解集（结果保留1位小数，误差不超0.2）

查看试题解析

24. 材料1：若将一个自然数各数位上的数字按照从高位到低位排成一列后，后一个数减去前一个数的差是一个常数，则这个自然数叫做“进阶数”.如：四位数1357排列后为：1，3，5，7，因为7﹣5＝5﹣3＝3﹣1＝2，且差为2的常数，故1357是一个差为2的四位“进阶数”.又如，9876，3333也是“进阶数”.
材料2：若一个自然数从左到右各数位上的数字与另一个自然数从右到左各数位上的数字完全相同，则这两个自然数互为“翻转数”.例如：1357与7531，987与789，……，它们都互为“翻转数”.

规定：把最高位数字为x（1≤x≤5，且x为整数），差为2的三位“进阶数”与它的“翻转数”的和与222的商记为F（x）.例如，当5＝x时，三位“进阶数”为579，它的“翻转数”为975，则F（x）＝ $\frac{579 + 975}{222}$ ＝7，所以F（5）＝7

(1)、计算：F（1），F（4）；

(2)、规定：k＝F（m）﹣F（n），当F＝F（m）＋F（n）＝11时，求k的最小值.

查看试题解析
25. 如图，在平面直角坐标系中，抛物线y＝ax²﹣x＋c（a≠0）与x轴交于A（﹣1，0）、B（3，0）两点，直线AC与y轴交于点C，与抛物线交于点D，OA＝OC.

(1)、求该抛物线与直线AC的解析式；

(2)、若点E是x轴下方抛物线上一动点，连接AE、CE.求△ACE面积的最大值及此时点E的坐标；

(3)、将原抛物线沿射线AD方向平移2 $\sqrt{2}$ 个单位长度，得到新抛物线：y₁＝a₁x²＋b₁x＋c₁（a≠0），新抛物线与原抛物线交于点F，在直线AD上是否存在点P，使以点P、D、F为顶点的三角形是等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由.

查看试题解析
26. 如图，在Rt△ABC中，∠ABC＝90°，∠BAC＝30°，点D在直线BC上运动，连接AD，以AD为斜边在直线AD的右侧作Rt△ADE，其中∠AED＝90°，∠DAE＝30°.

(1)、如图1，点D运动到点B的左侧时，DE与AB相交于点O，当AO平分∠DAE时，若DC＝6，求AD的长；

(2)、如图2，点D沿射线BC方向运动过程中，当BD＝AB时，连接BE，过点B作BF⊥BE交EA的延长线于点F，取CD的中点G，连接EG.求证：DE＋AE＝ $\sqrt{6}$ EG；

(3)、如图3，点D沿射线CB方向运动过程中，连接BE，将线段BE绕点E顺时针方向旋转60°，得到线段EH，连接AH、CH.若AB＝6，当CH＋ $\frac{1}{2}$ AH取得最小值时，请直接写出△ABE的面积.

查看试题解析