浙江省杭州市萧山区2021年数学中考二模试卷
试卷更新日期:2021-09-06 类型:中考模拟
一、单选题
-
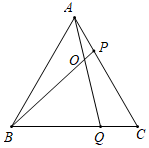
1. 下列运算,结果为正数的是( )A、 B、 C、 D、2. 一组数据-2, ,5,3,1有唯一的众数5,则这组数据的中位数是( )A、-2 B、1 C、3 D、53. 已知 ,则( )A、 B、 C、 D、4. 在平面直角坐标系中,点 与点 关于 轴对称,则( )A、 , B、 , C、 , D、 ,5. 如图,以点 为圆心作圆恰好与直线 相切,则与半径相等的线段是( )
 A、 B、 C、 D、6. 若 , ,则( )A、 B、 C、 D、7. 某商铺促销,单价80元的衬衫按照8折销售仍可获利10元,若这款衬衫的成本价为 元/件,则( )A、 B、 C、 D、8. 点 , , 是反比例函数 图象上的三个点,则 的大小关系是( )A、 B、 C、 D、9. 在菱形ABCD中,记∠ABC=∠α(0°<∠α<90°),菱形的面积记作S,菱形的周长记作C,若AD=2,则( )A、C与∠α的大小有关 B、当∠α=45°时,S= C、A,B,C,D四个点可以在同一个圆上 D、S随∠α的增大而增大10. 已知平面直角坐标系中的动点 , , 满足 , ,其中 ,给出下列说法:①动点 可以运动到原点;②动点 可以运动到第一象限;③动点 在 轴正半轴上;④动点 在第三象限,其中正确说法的序号是( )A、①② B、①③ C、②④ D、③④
A、 B、 C、 D、6. 若 , ,则( )A、 B、 C、 D、7. 某商铺促销,单价80元的衬衫按照8折销售仍可获利10元,若这款衬衫的成本价为 元/件,则( )A、 B、 C、 D、8. 点 , , 是反比例函数 图象上的三个点,则 的大小关系是( )A、 B、 C、 D、9. 在菱形ABCD中,记∠ABC=∠α(0°<∠α<90°),菱形的面积记作S,菱形的周长记作C,若AD=2,则( )A、C与∠α的大小有关 B、当∠α=45°时,S= C、A,B,C,D四个点可以在同一个圆上 D、S随∠α的增大而增大10. 已知平面直角坐标系中的动点 , , 满足 , ,其中 ,给出下列说法:①动点 可以运动到原点;②动点 可以运动到第一象限;③动点 在 轴正半轴上;④动点 在第三象限,其中正确说法的序号是( )A、①② B、①③ C、②④ D、③④二、填空题
-
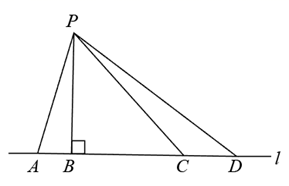
11. 的平方根是12. 不透明袋子中有1个红球和2个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,恰好是红球的概率为.13. 分解因式:a3﹣a= .14. 如图, , 是 的两条切线, , 为切点,若 , ,则 .
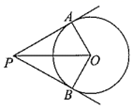 15. 如图所示,在边长相同的小正方形组成的网格中, 与 交于点 ,那么 .
15. 如图所示,在边长相同的小正方形组成的网格中, 与 交于点 ,那么 .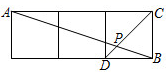 16. 如图,点 是平行四边形 边 上一点,将 沿直线 翻折,点 的对应点 恰好落在 的角平分线 上,若 , , ,则 , .
16. 如图,点 是平行四边形 边 上一点,将 沿直线 翻折,点 的对应点 恰好落在 的角平分线 上,若 , , ,则 , .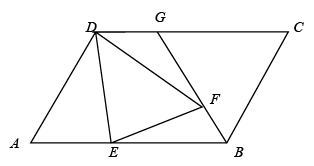
三、解答题
-
17. 下面是圆圆同学计算一道题的过程:
.
圆圆同学这样算正确吗?如果正确请解释理由;如果不正确,请你写出正确的计算过程.
18. 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b)。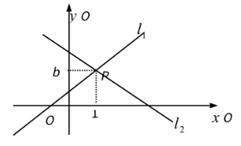 (1)、直接写出x+1>mx+n的解集;(2)、将y=x+1与y=mx+n组成方程组,不解方程组,请直接写出它的解.(3)、直线l3: y=nx+m是否也经过点P?请说明理由。19. 文具店购进了20盒“2B铅笔”,但在销售过程中发现其中混入了若干“HB铅笔”,店员进行统计后发现每盒铅笔中最多混入了2支“HB铅笔”,具体数据如下表:
(1)、直接写出x+1>mx+n的解集;(2)、将y=x+1与y=mx+n组成方程组,不解方程组,请直接写出它的解.(3)、直线l3: y=nx+m是否也经过点P?请说明理由。19. 文具店购进了20盒“2B铅笔”,但在销售过程中发现其中混入了若干“HB铅笔”,店员进行统计后发现每盒铅笔中最多混入了2支“HB铅笔”,具体数据如下表:混入“HB”铅笔数
0
1
2
盒数
6
m
n
(1)、用等式写出m、n满足的关系式;(2)、从20盒中任意选取1盒;①“盒子中没有混入HB铅笔”是 ▲ 事件;
②若“盒中混入1支HB铅笔”的概率为0.25,求m、n的值.
20. 某司机驾驶汽车从甲地去乙地,他以70 km/h的平均速度用3h到达目的地.(1)、当他按原路匀速返回时,汽车的速度 与时间 有怎样的函数关系?(2)、如果该司机返回到甲地的时间不超过2.5h,那么返程的平均速度不能小于多少?21. 如图,在四边形ABCD中,AD∥BC , ∠A=∠BDC .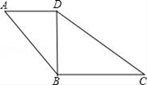 (1)、求证:△ABD∽△DCB;(2)、若AB=12,AD=8,CD=15,求DB的长.
(1)、求证:△ABD∽△DCB;(2)、若AB=12,AD=8,CD=15,求DB的长.