浙江省东阳市2021年数学初中学业水平模拟考试试卷
试卷更新日期:2021-09-06 类型:中考模拟
一、单选题
-
1. 如果向南走2km记作+2km,那么-3km表示( ).A、向东走3km B、向北走3km C、向西走3km D、向南走3km2. 义东高速公路东阳段是今年省重点建设项目,路线全长 ,按双向六车道高速公路标准设计,总投资100.8亿元其中数据100.8亿用科学记数法表示为( )A、 B、 C、 D、3. 下面的几何图形是由四个相同的小正方体搭成的,其中主视图和左视图相同的是( )A、
 B、
B、 C、
C、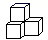 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 解分式方程 时,去分母正确的是( )A、 B、 C、 D、6. 今年是建党100周年,15名同学参加党知识竞赛的成绩如下表所示:
4. 下列计算正确的是( )A、 B、 C、 D、5. 解分式方程 时,去分母正确的是( )A、 B、 C、 D、6. 今年是建党100周年,15名同学参加党知识竞赛的成绩如下表所示:成绩
75
80
85
90
95
100
人数
1
2
4
3
3
2
这些同学党知识竞赛成绩的中位数和众数分别是( )
A、85,85 B、90,85 C、87.5,85 D、90,907. 如图,在 的网格中,每个小正方形的边长为1, 均在格点上, 与 之间的距离为( ) A、 B、2 C、 D、8. 设正比例函数y=mx的图象经过点A(m , 4),且y的值随x值的增大而减小,则m=( )A、2 B、-2 C、4 D、-49. 将正方形纸片按图①方式依次对折得图②的 ,点D是 边上一点,沿线段 剪开,展开后得到一个正八边形,则点D应满足( )
A、 B、2 C、 D、8. 设正比例函数y=mx的图象经过点A(m , 4),且y的值随x值的增大而减小,则m=( )A、2 B、-2 C、4 D、-49. 将正方形纸片按图①方式依次对折得图②的 ,点D是 边上一点,沿线段 剪开,展开后得到一个正八边形,则点D应满足( ) A、 B、 C、 D、10. 如图, 与 均为等边三角形,O为 的中点,点D在边 上,则 的值为( )
A、 B、 C、 D、10. 如图, 与 均为等边三角形,O为 的中点,点D在边 上,则 的值为( ) A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
11. 因式分解: .12. 一个布袋里装有只有颜色不同的3个球,其中一个红球两个白球,从中任意摸出一个球记下颜色后放回,搅匀,再摸出一个球,则摸出的两个球都是白球的概率为.13. 如图,圆锥的底面半径 ,高 ,则圆锥的侧面积等于.
 14. 如图,OP平分∠MON,A是边OM上一点,以点A为圆心、大于点A到ON的距离为半径作弧,交ON于点B、C,再分别以点B、C为圆心,大于 BC的长为半径作弧,两弧交于点D、作直线AD分别交OP、ON于点E、F.若∠MON=60°,EF=1,则OA= .
14. 如图,OP平分∠MON,A是边OM上一点,以点A为圆心、大于点A到ON的距离为半径作弧,交ON于点B、C,再分别以点B、C为圆心,大于 BC的长为半径作弧,两弧交于点D、作直线AD分别交OP、ON于点E、F.若∠MON=60°,EF=1,则OA= .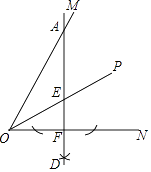 15. 如图,二次函数 的图象经过一个顶点在原点的正方形的另三个顶点,则 .
15. 如图,二次函数 的图象经过一个顶点在原点的正方形的另三个顶点,则 . 16. 将一个较短直角边 的直角三角形纸片沿斜边上的高线 分割成两个小的直角三角形(如图1),将得到的两个直角三角形按图2叠放( 在 边上),当 与点D重合时,图3中两个阴影部分的面积相等.
16. 将一个较短直角边 的直角三角形纸片沿斜边上的高线 分割成两个小的直角三角形(如图1),将得到的两个直角三角形按图2叠放( 在 边上),当 与点D重合时,图3中两个阴影部分的面积相等. (1)、图3中有个等腰三角形.(2)、记两个直角三角形重叠部分的面积为S,则S的取值范围是.
(1)、图3中有个等腰三角形.(2)、记两个直角三角形重叠部分的面积为S,则S的取值范围是.三、解答题
-
17. 计算:18. 解方程:19. 如图 是直三棱柱立柜横截面,立柜的上、下底面是一个等腰直角三角形,腰长为 ,小刚和小强要将这个立柜搬过宽为 的通道( 之间的距离为 ).

 (1)、小刚计算了 中 边上高为m,就知道立柜能搬过这个通道.(2)、小强发现,柜子稍作倾斜,只要满足 都能通过,求m的值.20. 如图,在 中,点O在斜边 上,以O为圆心, 为半径作圆,分别与 相交于点 ,连结 ,作弦 ,垂足为点H,已知 .
(1)、小刚计算了 中 边上高为m,就知道立柜能搬过这个通道.(2)、小强发现,柜子稍作倾斜,只要满足 都能通过,求m的值.20. 如图,在 中,点O在斜边 上,以O为圆心, 为半径作圆,分别与 相交于点 ,连结 ,作弦 ,垂足为点H,已知 . (1)、求证: 是 的切线.(2)、若 ,求弦 的长.21. 已知:如图, 的边 在x轴上, ,点B为 ,抛物线 经过点 ,点P为 的对称中心.
(1)、求证: 是 的切线.(2)、若 ,求弦 的长.21. 已知:如图, 的边 在x轴上, ,点B为 ,抛物线 经过点 ,点P为 的对称中心. (1)、求此抛物线的函数表达式.(2)、平移抛物线,能否使平移后的抛物线同时经过点P,点C?若能,请写出平移方式,并说明理由.22. 五一假期,某旅行团32人在秦王宫景区游玩,他们由成人和儿童组成.已知成人比儿童多12人.(1)、求该旅行团中成人与儿童分别是多少人?(2)、因时间充裕,该团准备让部分成人带领全部儿童去清明上河图景区游玩,清明上河图景区的门票价格为160元/张,成人全票,儿童5折,一名成人可以免费携带一名儿童.并且为安全起见,一个成人最多监护两个儿童.
(1)、求此抛物线的函数表达式.(2)、平移抛物线,能否使平移后的抛物线同时经过点P,点C?若能,请写出平移方式,并说明理由.22. 五一假期,某旅行团32人在秦王宫景区游玩,他们由成人和儿童组成.已知成人比儿童多12人.(1)、求该旅行团中成人与儿童分别是多少人?(2)、因时间充裕,该团准备让部分成人带领全部儿童去清明上河图景区游玩,清明上河图景区的门票价格为160元/张,成人全票,儿童5折,一名成人可以免费携带一名儿童.并且为安全起见,一个成人最多监护两个儿童.①若由成人8人带队,则所需门票的总费用是多少元?
②若剩余经费只有1400元可用于购票,在不超额的前提下,可以安排多少成人带队?求所有满足条件的方案.

