贵州省遵义市红花岗区2021年数学中考二模试卷

试卷更新日期：2021-09-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数2021的相反数是（）

A、2021 B、-2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
2. 为全力抗击“新冠肺炎”疫情，响应政府“停课不停学”号召，在疫情防控期间，教师们纷纷通过网络平台坚持教学，下面是一些网络平台的图标，在这些图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 习近平在全国脱贫攻坚总结表彰大会上庄严宣告，我国脱贫攻坚战取得了全面胜利，现行标准下9899万农村贫困人口全部脱贫，832个贫困县全部摘帽，12.8万个贫困村全部出列，完成了消除绝对贫困的艰巨任务，创造了又一个彪炳史册的人间奇迹！9899万用科学记数法表示为（）

A、 $0.9899 \times 10^{8}$ B、 $9.899 \times 10^{8}$ C、 $9.899 \times 10^{7}$ D、 $98.99 \times 10^{6}$

查看试题解析
4. 下列计算正确的是（）

A、 ${(a + b)}^{2} = a^{2} + b^{2}$ B、 ${(- 2 x^{2})}^{3} = - 8 x^{6}$ C、 $x^{2} y \div \frac{1}{y} = x^{2} (y \neq 0)$ D、 $a^{2} + 2 a^{2} = 3 a^{4}$

查看试题解析
5. 某次校运会共有13名同学报名参加百米赛跑，他们的预赛成绩各不相同，现取其中前6名参加决赛，小勇同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这13名同学成绩的（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
6. 如图，已知直线 $a // b$ ，直角三角形 $A B C$ 中， $∠ C = 90 °$ ，若 $∠ B = 58 °$ ，那么 $∠ 1 - ∠ 2 =$ （）

A、28° B、30° C、32° D、58°

查看试题解析
7. 小幸学习了在数轴上画出表示无理数的点的方法后，进行以下练习：首先画出数轴，原点为O，在数轴上找到表示数2的点A，然后过点A作AB⊥OA，使AB＝3．以点O为圆心，OB为半径作弧，交数轴正半轴于点P，则点P所表示的数介于（　　）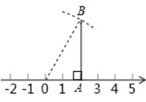

A、3和3.5之间 B、3.5和4之间 C、4和4.5之间 D、4.5和5之间

查看试题解析
8. 若 $x_{1}$ 和 $x_{2}$ 为一元二次方程 $x^{2} + 2 x - 1 = 0$ 的两个根，则 $x_{1}^{2} x_{2} + x_{1} x_{2}^{2}$ 的值为（）

A、2 B、3 C、4 D、 $4 \sqrt{2}$

查看试题解析
9. 背面图案、形状大小都相同的四张卡片的正面分别记录着有关函数 $y = 2 x - 4$ 的四个结论，现将卡片背面朝上，随机抽取一张，抽到卡片上的结论正确的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
10. 如图，已知正五边形 $A B C D E$ 和正 $△ C D F$ ，则 $∠ A F E$ 的度数为（）

A、42° B、48° C、66° D、84°

查看试题解析
11. 如图，有10个形状大小一样的小长方形①，将其中的3个小长方形①放入正方形②中，剩余的7个小长方形①放入长方形③中，其中正方形②中的阴影部分面积为22，长方形③中的阴影部分面积为96，那么一个小长方形①的面积为（）

A、5 B、6 C、9 D、10

查看试题解析
12. 如图，已知菱形A $B C D$ ， $E$ 、 $F$ 、 $G$ 、 $H$ 分别是 $A B$ 、 $B C$ 、 $C D$ 、 $D A$ 边上的点，且满足 $A H = B E = C F = D G = \frac{1}{3} A B$ ，则四边形 $E F G H$ 与菱形 $A B C D$ 的面积比为（）

A、 $\frac{4}{9}$ B、 $\frac{5}{9}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{2}{3}$

查看试题解析

二、填空题

13. 计算： $\sqrt{18} - 2 \sqrt{\frac{1}{2}}$ ＝．

查看试题解析
14. 已知点 $A (m ， n)$ 在双曲线 $y = \frac{k}{x}$ 上，点 $B (- m ， n)$ 在直线 $y = 2 x - 3 k$ 上，则 $\frac{2}{n} + \frac{1}{m}$ 的值为.

查看试题解析
15. 如图，以平行四边形 $A B C D$ 的顶点 $A$ 为圆心， $A B$ 边为半径画弧 $B E$ ，交 $A D$ 边于 $E$ ， $B E$ 弧所在的圆与边 $C D$ 相切于点 $C$ ，若 $A B = 4$ ，则图中阴影部分的面积为.

查看试题解析
16. 如图，已知 $A B$ 是 $⊙ O$ 的直径，且 $A B = 6 \sqrt{3}$ ，弦 $C D ⊥ A B$ ，点 $E$ 是弧 $B C$ 上的点，连接 $A E$ 、 $D E$ ，若 $∠ A + ∠ D = 30 °$ ，则 $C D$ 的长为.

查看试题解析

三、解答题

17.

(1)、计算： $| \sqrt{2} - 3 | + 2 \cos 45 ° + {(- \frac{1}{2})}^{- 2}$

(2)、解分式方程： $\frac{2 x + 1}{x + 3} - 2 = \frac{2}{3 - x}$

查看试题解析
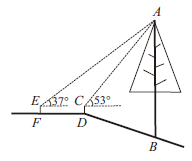
18. 先化简 $(x + 3 - \frac{7}{x - 3}) \div \frac{2 x^{2} - 8 x}{x - 3}$ ，再从 $0 \leq x \leq 4$ 中选一个适合的整数代入求值.

查看试题解析
19. 如图，某山区山坡上有一颗树 $A B$ 与水平面垂直，某数学兴趣小组为了测量其高度，在斜坡边缘 $D$ 处安装了测倾器 $C D$ ，测得树的顶端 $A$ 的仰角为 $53 °$ ，将测倾器向后移动5.6米，安装在 $F$ 点处，测得顶端 $A$ 的仰角为 $37 °$ ，已知此山坡的坡度为 $1 ： 3$ ，测倾器的高 $C D = E F = 0.5$ 米， $F$ 、 $D$ 在同一水平线上，且 $E F$ 、 $C D$ 均垂直于 $F D$ ，求这棵树的高 $A B$ .（参考数据： $\sin 37 ° = \frac{3}{5}$ ， $\cos 37 ° = \frac{4}{5}$ ， $\tan 37 ° = \frac{3}{4}$ ， $\sin 53 ° = \frac{4}{5}$ ， $\cos 53 ° = \frac{3}{5}$ ， $\tan 53 ° = \frac{4}{3}$ ）

查看试题解析
20. 如图，四边形 $A B C D$ 为正方形， $E$ 为 $A D$ 上点，连接 $B E$ ， $∠ A E B = 60 °$ ， $M$ 为 $B E$ 的中点，过点 $M$ 的直线交 $A B$ 、 $C D$ 于 $P$ 、 $Q$ .

(1)、如图1，当 $P Q ⊥ B E$ 时，求证： $B P = 2 A P$ ；

(2)、如图2，若 $∠ A P Q$ 为锐角，且 $P Q = B E$ ，延长 $B E$ 、 $C D$ 交于点 $N$ ，请你猜想 $Q M$ 与 $Q N$ 的数量关系，并说明理由；

查看试题解析
21. 为了迎接体育中考，某校对600名毕业班学生进行了一次体能摸底测试（满分30分），并随机抽取部分学生的测试成绩（单位：分），制成如下图所示的频数分布直方图，已知成绩在15.5~18.5这一组的频率为0.05.请回答下列问题：

(1)、在这个调查中，样本容量为，学生体育测试的平均成绩是（提示：取各组的组中值进行计算）；

(2)、补全成绩在21.5~24.5这组的频数分布直方图；

(3)、学校准备从测试成绩在27.5~30.5这一组同学中，选2名同学当体育集训的督导员，但只有5名同学自愿报名，且5名同学中男生比女生多1名，若学校采取随机抽签的方式确定两名同学，求选中的同学恰好是一男一女的概率.

查看试题解析
22. 甲、乙两家工厂计划每天各生产6万只口罩，但由于转型条件不同，其生产的成本不一样，甲工厂每生产1万只口罩的成本为0.6万元，乙工厂每生产1万只口罩的成本为0.8万元.

(1)、按照计划，甲、乙两家工厂共生产2000万只口罩，且甲工厂生产口罩的总成本不高于乙工厂生产口罩的总成本的 $\frac{3}{4}$ ，求甲工厂最多可生产多少万只口罩？

(2)、实际生产时，甲工厂完全按计划执行，但乙工厂的生产情况发生了一些变化，乙工厂实际每天比计划多生产 $0.1 m (m > 0)$ 万只口罩，每生产1万只口罩的成本比计划少 $0.02 m$ 万元，最终乙工厂实际每天生产口罩的成本比计划少0.25万元，求 $m$ 的值.

查看试题解析
23. 如图1，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴相交于 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C (0 ， 3)$ ，抛物线的顶点 $D$ 的坐标为 $(1 ， 4)$ ，点 $P$ 为第一象限内抛物线上一动点（点 $P$ 与顶点 $D$ 不重合）.

(1)、求抛物线的解析式及 $A$ 、 $B$ 两点的坐标；

(2)、如图1，过点 $P$ 作 $P M ⊥ x$ 轴于 $M$ ，交 $B C$ 于点 $N$ ，若点 $N$ 是 $P M$ 的三等分点，求此时 $P$ 的坐标；

(3)、如图2，当点 $P$ 在抛物线对称轴的右侧时，过点 $P$ 作 $P Q ⊥ A D$ 于点 $Q$ ，设抛物线对称轴与 $x$ 轴交于点 $H$ ，是否存在这样的点 $P$ ，以 $P$ 、 $D$ 、 $Q$ 为顶点的三角形与 $△ A D H$ 相似？若存在，求出 $P$ 点的坐标，若不存在，请说明理由.

查看试题解析
24. 新定义：有一组邻边相等且对角互补的四边形叫做等补四边形.如图1，在四边形 $A B C D$ 中， $A D = C D$ ， $∠ B A D + ∠ B C D = 180 °$ ，则四边形 $A B C D$ 是一个等补四边形.在数学活动课上，巧巧小组对等补四边形 $A B C D$ 进一步探究，发现 $B D$ 平分 $∠ A B C$ .

(1)、巧巧小组提供的解题思路是：如图2，过点 $D$ 分别作 $D E ⊥ B C$ 于 $E$ ， $D F ⊥ B A$ 交 $B A$ 的延长线于 $F$ ，通过证明 $△ A D F ≌ △ C D E$ ，得 $D F = D E$ ，再根据“角的内部到角的两边的距离相等的点在角的平分线上”得到 $B D$ 平分 $∠ A B C$ .请你写出巧巧小组的完整证明过程；

(2)、如图3，在平面直角坐标系中，点 $A$ 、 $B$ 在 $x$ 轴上，以 $A B$ 为直径的 $⊙ M$ 交 $y$ 轴于点 $C$ 、 $D$ ，点 $P$ 为弧 $B C$ 上一动点（不与 $B$ 、 $C$ 重合），求证：四边形 $A C P D$ 始终是一个等补四边形；

(3)、在（2）的条件下，如图4，已知 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，巧巧小组提出了一个问题：连接 $P A$ ， $P C + P D$ 与 $P A$ 的比值是否会随着点 $P$ 的移动而变化？若不变化，请求出其比值；若变化，请说明理由.

查看试题解析