福建厦门同安区2021年数学中考三模试卷
试卷更新日期:2021-09-06 类型:中考模拟
一、单选题
-
1. 下列计算结果等于﹣1的是( )A、﹣1+2 B、(﹣1)0 C、﹣12 D、(﹣1)﹣22. 按照我国《生活垃圾管理条例》要求,到2025年底,我国地级及以上城市要基本建设垃圾类处理系统,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,把一个直角三角尺的直角顶点放在直尺的一边上,则∠1与∠2之间关系一定成立的是( )
3. 如图,把一个直角三角尺的直角顶点放在直尺的一边上,则∠1与∠2之间关系一定成立的是( ) A、∠1=2∠2 B、∠1+∠2=180° C、∠1=∠2 D、∠1+∠2=90°4. 下列运算中,正确的是( )A、(ab2)2=a2b4 B、a2+a2=2a4 C、 D、a6÷a3=a25. 小红同学对数据25,32,23,25,4■,43进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、中位数 B、平均数 C、众数 D、方差6. 如图,数轴上的点 对应的数为 ,则数轴上与数 对应的点可能是( )
A、∠1=2∠2 B、∠1+∠2=180° C、∠1=∠2 D、∠1+∠2=90°4. 下列运算中,正确的是( )A、(ab2)2=a2b4 B、a2+a2=2a4 C、 D、a6÷a3=a25. 小红同学对数据25,32,23,25,4■,43进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、中位数 B、平均数 C、众数 D、方差6. 如图,数轴上的点 对应的数为 ,则数轴上与数 对应的点可能是( ) A、点 B、点 C、点 D、点7. 我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三:人出七,不足四,问人数、物价几何?”意思是:现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱:如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?设有x人,物品的价格为y元,可列方程(组)为( )
A、点 B、点 C、点 D、点7. 我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三:人出七,不足四,问人数、物价几何?”意思是:现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱:如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?设有x人,物品的价格为y元,可列方程(组)为( )
A、 B、 C、 D、 =8. 如图,一块长方体砖块的长、宽、高的比为 ,如果左视面向下放在地上,地面所受压强为 ,则正视面向下放在地上时,地面所受压强为( )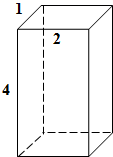 A、 B、 C、 D、9. 如图,点A、B、C在 上, ,垂足分别为D、E,若 ,则 的度数为( )
A、 B、 C、 D、9. 如图,点A、B、C在 上, ,垂足分别为D、E,若 ,则 的度数为( )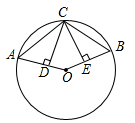 A、 B、 C、 D、10. 已知二次函数 ( 为常数)的图象与x轴有交点,且当 时,y随x的增大而增大,则a的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知二次函数 ( 为常数)的图象与x轴有交点,且当 时,y随x的增大而增大,则a的取值范围是( )A、 B、 C、 D、二、填空题
-
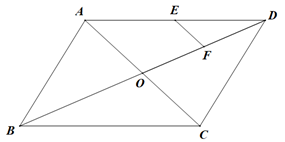
11. 预计到2025年,中国5G用户将超过460 000 000,将460 000 000用科学记数法表示为.12. 如图,在 中,对角线 , 相交于点 ,点 , 分别是 , 的中点,若 ,则 的长是.
 13. 不等式组: 的解集是.14. 4月23日是世界读书日,这天某校为了解学生课外阅读情况,随机收集了30名学生每周课外阅读的时间,统计如下:
13. 不等式组: 的解集是.14. 4月23日是世界读书日,这天某校为了解学生课外阅读情况,随机收集了30名学生每周课外阅读的时间,统计如下:阅读时间( 小时)
人数
12
8
6
4
则每周课外阅读时间在5小时以上的学生概率是.
15. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .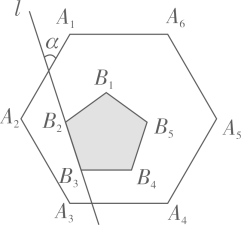 16. 如图,点D是平行四边形OABC内一点,CD与x轴平行,BD与y轴平行,BD= ,∠ADB=135°,S△ABD=2,若反比例函数y= (x>0)的图象经过A、D两点,则k的值是
16. 如图,点D是平行四边形OABC内一点,CD与x轴平行,BD与y轴平行,BD= ,∠ADB=135°,S△ABD=2,若反比例函数y= (x>0)的图象经过A、D两点,则k的值是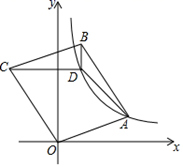
三、解答题
-
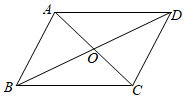
17. 解方程组 .18. 如图,四边形ABCD中,AD∥BC ,AC、BD相交于点O,O是AC的中点.
求证:四边形ABCD是平行四边形.
 19. 先化简,再求值: ,其中x= .20.(1)、如图,在 中, ,请在 边上求作一点 ,使 (要求:尺规作图,保留作图痕迹,不写作法);
19. 先化简,再求值: ,其中x= .20.(1)、如图,在 中, ,请在 边上求作一点 ,使 (要求:尺规作图,保留作图痕迹,不写作法);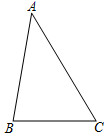 (2)、若 平分 ,且 , ,求 的长.21. “大美武汉·诗意江城”,某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校3000名学生中的部分学生,提供四个景点选择:A、黄鹤楼;B、东湖海洋世界;C、极地海洋世界;D、欢乐谷.要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
(2)、若 平分 ,且 , ,求 的长.21. “大美武汉·诗意江城”,某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校3000名学生中的部分学生,提供四个景点选择:A、黄鹤楼;B、东湖海洋世界;C、极地海洋世界;D、欢乐谷.要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图: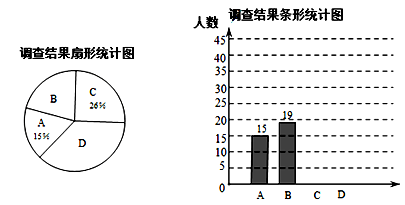
请根据图中提供的信息,解答下列问题:
(1)、一共调查了学生人(2)、扇形统计图中表示“最想去的景点D”的扇形圆心角为度(3)、如果A、B、C、D四个景点提供给学生优惠门票价格分别为20元、30元、40元、60元,根据以上的统计估计全校学生到对应的景点所需要门票总价格是多少元?22. 如图,在平行四边形ABCD中,∠D=60°,对角线AC⊥BC,⊙O经过点A,B,与AC交于点M,连接AO并延长与⊙O交于点F,与CB的延长线交于点E,AB=EB. (1)、求证:EC是⊙O的切线;(2)、若AD=2 ,求 的长(结果保留π).23. 一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
(1)、求证:EC是⊙O的切线;(2)、若AD=2 ,求 的长(结果保留π).23. 一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:x(元/件)
4
5
6
y(件)
10000
9500
9000
(1)、求y与x的函数关系式(不求自变量的取值范围);(2)、在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)、抗疫期间,该商场这种商品售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠m元( ),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.24. 在 中, , ,点 为线段 延长线上一动点,连接 ,将线段 绕点 逆时针旋转,旋转角为 ,得到线段 ,连接 , .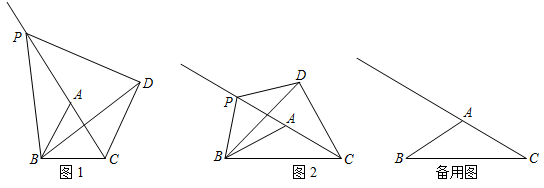 (1)、如图1,当 时,求证: ;(2)、如图2,当 时,猜想 和 的数量关系并说明理由.(3)、当 时,若 , ,求出点 到 的距离.25. 已知抛物线 的图象过点A(3,m).
(1)、如图1,当 时,求证: ;(2)、如图2,当 时,猜想 和 的数量关系并说明理由.(3)、当 时,若 , ,求出点 到 的距离.25. 已知抛物线 的图象过点A(3,m). (1)、当a=-1,m=0时,求抛物线的顶点坐标;(2)、若P(t,n)为该抛物线上一点,且n<m,求t的取值围;(3)、如图,直线 交抛物线于B,C两点,点Q(x,y)是抛物线上点B,C之间的一个动点,作QD⊥x轴交直线 l于点D,作QE⊥y轴于点E,连接DE.设∠QED=b,当 时,b 恰好满足 ,求a的值.
(1)、当a=-1,m=0时,求抛物线的顶点坐标;(2)、若P(t,n)为该抛物线上一点,且n<m,求t的取值围;(3)、如图,直线 交抛物线于B,C两点,点Q(x,y)是抛物线上点B,C之间的一个动点,作QD⊥x轴交直线 l于点D,作QE⊥y轴于点E,连接DE.设∠QED=b,当 时,b 恰好满足 ,求a的值.