西藏2021年中考数学试卷

试卷更新日期：2021-09-06 类型：中考真卷

进入出卷网下载

一、单选题

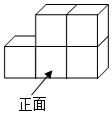
1. ﹣10的绝对值是（）

A、 $\frac{1}{10}$ B、﹣ $\frac{1}{10}$ C、10 D、﹣10

查看试题解析
2. 2020年12月3日.中共中央政治局常务委员会召开会议，听取脱贫攻坚总结评估汇报.中共中央总书记习近平主持会议并发表重要讲话.指出经过8年持续奋斗，我们如期完成了新时代脱贫攻坚目标任务，现行标准下农村贫困人口全部脱贫，贫困县全部摘帽，消除了绝对贫困和区域性整体贫困，近1亿贫困人口实现脱贫，取得了令全世界刮目相看的重大胜利.将100000000用科学记数法表示为（）

A、 0.1×10⁸ B、1×10⁷ C、1×10⁸ D、10×10⁸

查看试题解析
3. 如图是由五个相同的小正方体组成的几何体，其主视图为（）

A、 B、 C、 D、

查看试题解析
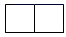4. 数据3，4，6，6，5的中位数是（）

A、4.5 B、5 C、5.5 D、6

查看试题解析
5. 下列计算正确的是（）

A、（a²b）³＝a⁶b³ B、a²＋a＝a³ C、a³•a⁴＝a¹² D、a⁶÷a³＝a²

查看试题解析
6. 把一块等腰直角三角板和一把直尺按如图所示的位置构成，若∠1＝25°，则∠2的度数为（）

A、15° B、20° C、25° D、30°

查看试题解析
7. 如图，在矩形ABCD中，对角线AC与BD相交于点O.点E、F分别是AB，AO的中点，且AC＝8，则EF的长度为（）

A、2 B、4 C、6 D、8

查看试题解析
8. 如图，△BCD内接于⊙O，∠D＝70°，OA⊥BC交⨀O于点A，连接AC，则∠OAC的度数为（）

A、40° B、55° C、70° D、110°

查看试题解析
9. 已知一元二次方程x²﹣10x＋24＝0的两个根是菱形的两条对角线长，则这个菱形的面积为（）

A、6 B、10 C、12 D、24

查看试题解析
10. 将抛物线y＝（x﹣1）²＋2向左平移3个单位长度，再向下平移4个单位长度所得到的抛物线的解析式为（）

A、y＝x²﹣8x＋22 B、y＝x²﹣8x＋14 C、y＝x²＋4x＋10 D、y＝x²＋4x＋2

查看试题解析
11. 如图.在平面直角坐标系中，△AOB的面积为 $\frac{27}{8}$ ，BA垂直x轴于点A，OB与双曲线y＝ $\frac{k}{x}$ 相交于点C，且BC∶OC＝1∶2，则k的值为（）

A、﹣3 B、﹣ $\frac{9}{4}$ C、3 D、 $\frac{9}{2}$

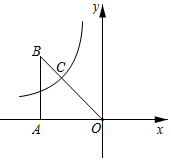查看试题解析
12. 如图，在Rt△ABC中，∠A＝30°，∠C＝90°，AB＝6，点P是线段AC上一动点，点M在线段AB上，当AM＝ $\frac{1}{3}$ AB时，PB＋PM的最小值为（）

A、3 $\sqrt{3}$ B、2 $\sqrt{7}$ C、2 $\sqrt{3}$ ＋2 D、3 $\sqrt{3}$ ＋3

查看试题解析

二、填空题

13. 若 $\sqrt{2 x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
14. 计算：（π﹣3）⁰＋（﹣ $\frac{1}{2}$ ）^﹣²﹣4sin30°＝.

查看试题解析
15. 若一个圆锥的底面半径为2，母线长为6，则该圆锥侧面展开图的圆心角是°．

查看试题解析
16. 若关于x的分式方程 $\frac{2 x}{x - 1}$ ﹣1＝ $\frac{m}{x - 1}$ 无解，则m＝.

查看试题解析
17. 如图.在Rt△ABC中，∠A＝90°，AC＝4.按以下步骤作图：（1）以点B为圆心，适当长为半径画弧，分别交线段BA，BC于点M，N；（2）以点C为圆心，BM长为半径画弧，交线段CB于点D；（3）以点D为圆心，MN长为半径画弧，与第2步中所面的弧相交于点E；（4）过点E画射线CE，与AB相交于点F.当AF＝3时，BC的长是.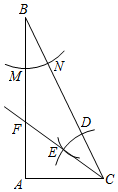

查看试题解析
18. 按一定规律排列的一列数依次为 $\frac{2}{3}$ ， $\frac{1}{4}$ ， $\frac{2}{15}$ ， $\frac{1}{12}$ ， $\frac{2}{35}$ ，…，按此规律排列下去，这列数中的第n个数是.

查看试题解析

三、解答题

19. 解不等式组 ${\begin{matrix} 2 x + 3 > 1 \\ \frac{2 x - 1}{3} \leq \frac{x}{2} \end{matrix}$ ，并把解集在数轴上表示出来.

查看试题解析
20. 先化简，再求值： $\frac{a^{2} + 2 a + 1}{a - 2}$ • $\frac{a - 2}{a^{2} - 1}$ ﹣（ $\frac{1}{a - 1}$ ＋1），其中a＝10.

查看试题解析
21. 如图，AB∥DE，B，C，D三点在同一条直线上，∠A＝90°，EC⊥BD，且AB＝CD.求证：AC＝CE.

查看试题解析
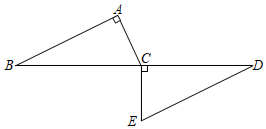22. 列方程（组）解应用题
为振兴农村经济，某县决定购买A，B两种药材幼苗发给农民栽种，已知购买2棵A种药材幼苗和3棵B种药材幼苗共需41元.购买8棵A种药材幼苗和9棵B种药材幼苗共需137元.问每棵A种药材幼苗和每棵B种药材幼苗的价格分别是多少元？

查看试题解析
23. 为铸牢中华民族共同体意识，不断巩固民族大团结，红星中学即将举办庆祝建党100周年“中华民族一家亲，同心共筑中国梦”主题活动.学校拟定了演讲比赛、文艺汇演、书画展览、知识竞赛四种活动方案，为了解学生对活动方案的喜爱情况，学校随机抽取了200名学生进行调查（每人只能选择一种方案），将调结果绘制成如下两幅不完整的统计图，请你根据以下两幅图所给的信息解答下列问题.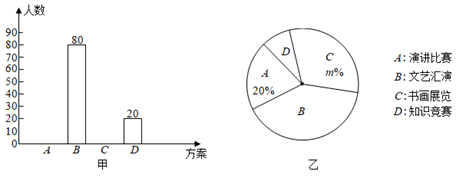

(1)、在抽取的200名学生中，选择“演讲比赛”的人数为，在扇形统计图中，m的值为.

(2)、根据本次调查结果，估计全校2000名学生中选择“文艺汇演”的学生大约有多少人？

(3)、现从喜爱“知识竞赛”的四名同学a、b、c、d中，任选两名同学参加学校知识竞赛，请用树状图或列表法求出a同学参加的概率.

查看试题解析
24. 已知第一象限点P(x，y)在直线y＝﹣x＋5上，点A的坐标为(4，0)，设△AOP的面积为S.

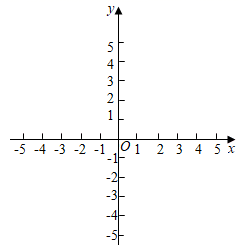(1)、当点P的横坐标为2时，求△AOP的面积；

(2)、当S＝4时，求点P的坐标；

(3)、求S关于x的函数解析式，写出x的取值范围，并在图中画出函数S的图象.

查看试题解析
25. 如图，为了测量某建筑物CD的高度，在地面上取A，B两点，使A、B、D三点在同一条直线上，拉姆同学在点A处测得该建筑物顶部C的仰角为30°，小明同学在点B处测得该建筑物顶部C的仰角为45°，且AB＝10m.求建筑物CD的高度.（拉姆和小明同学的身高忽略不计.结果精确到0.1m， $\sqrt{3}$ ≈1.732）

查看试题解析
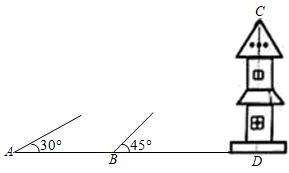26. 如图，AB是⊙O的直径，OC是半径，延长OC至点D.连接AD，AC，BC.使∠CAD＝∠B.

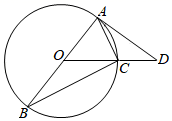(1)、求证：AD是⊙O的切线；

(2)、若AD＝4，tan∠CAD＝ $\frac{1}{2}$ ，求BC的长.

查看试题解析
27. 在平面直角坐标系中，抛物线y＝﹣x²＋bx＋c与x轴交于A，B两点.与y轴交于点C.且点A的坐标为（﹣1，0），点C的坐标为（0，5）.

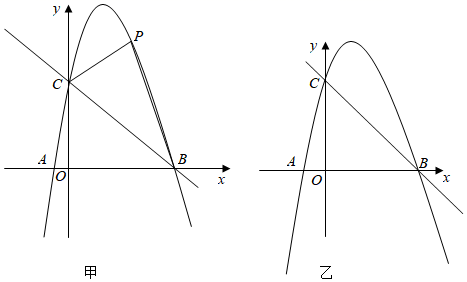(1)、求该抛物线的解析式；

(2)、如图（甲）.若点P是第一象限内抛物线上的一动点.当点P到直线BC的距离最大时，求点P的坐标；

(3)、图（乙）中，若点M是抛物线上一点，点N是抛物线对称轴上一点，是否存在点M使得以B，C，M，N为顶点的四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由.

查看试题解析