江苏省镇江市2021年中考数学试卷

试卷更新日期：2021-09-06 类型：中考真卷

进入出卷网下载

一、填空题

1. -5的绝对值是．

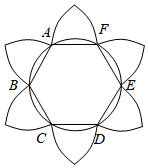
查看试题解析
2. 使 $\sqrt{x - 7}$ 有意义的x的取值范围是.

查看试题解析
3. 8的立方根是．

查看试题解析
4. 如图，花瓣图案中的正六边形ABCDEF的每个内角的度数是.

查看试题解析
5. 一元二次方程 $x (x + 1) = 0$ 的解是.

查看试题解析
6. 小丽的笔试成绩为100分，面试成绩为90分，若笔试成绩、面试成绩按6：4计算平均成绩，则小丽的平均成绩是分.

查看试题解析
7. 某射手在一次训练中共射出了10发子弹，射击成绩如图所示，则射击成绩的中位数是环.

查看试题解析
8. 如图，点D，E分别在△ABC的边AC，AB上，△ADE∽△ABC，M，N分别是DE，BC的中点，若 $\frac{A M}{A N}$ ＝ $\frac{1}{2}$ ，则 $\frac{S_{△ A D E}}{S_{△ A B C}}$ ＝.

查看试题解析
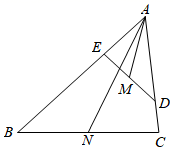9. 如图，点A，B，C，O在网格中小正方形的顶点处，直线l经过点C，O，将 $△$ ABC沿l平移得到 $△$ MNO，M是A的对应点，再将这两个三角形沿l翻折，P，Q分别是A，M的对应点.已知网格中每个小正方形的边长都等于1，则PQ的长为.

查看试题解析
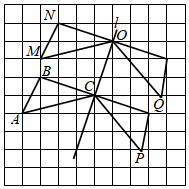10. 已知一次函数的图象经过点(1，2)，且函数值y随自变量x的增大而减小，写出符合条件的一次函数表达式.（答案不唯一，写出一个即可）

查看试题解析
11. 一只不透明的袋子中装有1个黄球，现放若干个红球，它们与黄球除颜色外都相同，搅匀后从中任意摸出两个球，使得P（摸出一红一黄）＝P（摸出两红），则放入的红球个数为.

查看试题解析
12. 如图，等腰三角形ABC中，AB＝AC，BC＝6，cos∠ABC＝ $\frac{1}{3}$ ，点P在边AC上运动（可与点A，C重合），将线段BP绕点P逆时针旋转120°，得到线段DP，连接BD，则BD长的最大值为.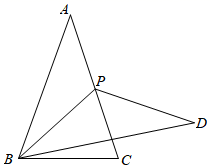

查看试题解析

二、单选题

13. 如图所示，该几何体的俯视图是（）

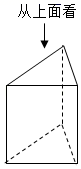A、正方形 B、长方形 C、三角形 D、圆

查看试题解析
14. 2021年1﹣4月份，全国规模以上工业企业利润总额超25900亿元，其中25900用科学记数法表示为（）

A、 25.9×10³ B、2.59×10⁴ C、0.259×10⁵ D、2.59×10⁵

查看试题解析
15. 如图，∠BAC＝36°，点O在边AB上，⊙O与边AC相切于点D，交边AB于点E，F，连接FD，则∠AFD等于（）

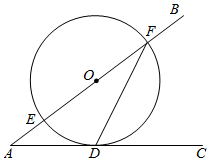A、27° B、29° C、35° D、37°

查看试题解析
16. 如图，输入数值1921，按所示的程序运算（完成一个方框内的运算后，把结果输入下一个方框继续进行运算），输出的结果为（）

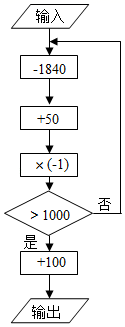A、1840 B、1921 C、1949 D、2021

查看试题解析
17. 设圆锥的底面圆半径为r，圆锥的母线长为l，满足2r+l＝6，这样的圆锥的侧面积（）

A、有最大值 $\frac{9}{4}$ π B、有最小值 $\frac{9}{4}$ π C、有最大值 $\frac{9}{2}$ π D、有最小值 $\frac{9}{2}$ π

查看试题解析
18. 如图，小明在3×3的方格纸上写了九个式子（其中的n是正整数），每行的三个式子的和自上而下分别记为A₁ ， A₂ ， A₃ ，每列的三个式子的和自左至右分别记为B₁ ， B₂ ， B₃ ，其中，值可以等于789的是（）

A、A₁ B、B₁ C、A₂ D、B₃

查看试题解析

三、解答题

19.

(1)、计算：（1﹣ $\sqrt{2}$ ）⁰﹣2sin45°+ $\sqrt{2}$ ；

(2)、化简：（x²﹣1）÷（1﹣ $\frac{1}{x}$ ）﹣x.

查看试题解析
20.

(1)、解方程： $\frac{3}{x}$ ﹣ $\frac{2}{x - 2}$ ＝0；

(2)、解不等式组： ${\begin{matrix} 3 x - 1 \geq x + 1 \\ x + 4 < 4 x - 2 \end{matrix}$ .

查看试题解析
21. 甲、乙、丙三人各自随机选择到A，B两个献血站进行爱心献血.求这三人在同一个献血站献血的概率.

查看试题解析
22. 如图，四边形ABCD是平行四边形，延长DA，BC，使得AE＝CF，连接BE，DF.

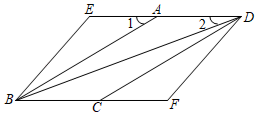(1)、求证： $△ A B E ≌ △ C D F$ ；

(2)、连接BD，∠1＝30°，∠2＝20°，当∠ABE＝°时，四边形BFDE是菱形.

查看试题解析
23. 《九章算术》被历代数学家尊为“算经之首”.下面是其卷中记载的关于“盈不足”的一个问题：今有共买金，人出四百，盈三千四百；人出三百，盈一百.问人数、金价各几何？这段话的意思是：今有人合伙买金，每人出400钱，会剩余3400钱；每人出300钱，会剩余100钱.合伙人数、金价各是多少？请解决上述问题.

查看试题解析

24. 如表是第四至七次全国人口普查的相关数据.

年份	我国大陆人口总数	其中具有大学文化程度的人数	每10万大陆人口中具有大学文化程度的人数
1990年	1133682501	16124678	1422
2000年	1265830000	45710000	3611
2010年	1339724852	119636790	8930
2020年	1411778724	218360767	15467

(1)、设下一次人口普查我国大陆人口共a人，其中具有大学文化程度的有b人，则该次人口普查中每10万大陆人口中具有大学文化程度的人数为；（用含有a，b的代数式表示）

(2)、如果将2020年大陆人口中具有各类文化程度（含大学、高中、初中、小学、其他）的人数分布制作成扇形统计图，求其中表示具有大学文化程度类别的扇形圆心角的度数；（精确到1°）

(3)、你认为统计“每10万大陆人口中具有大学文化程度的人数”这样的数据有什么好处？（写出一个即可）

查看试题解析

25. 如图，点A和点E(2，1)是反比例函数y＝ $\frac{k}{x}$ （x＞0）图象上的两点，点B在反比例函数y＝ $\frac{6}{x}$ （x＜0）的图象上，分别过点A，B作y轴的垂线，垂足分别为点C，D，AC＝BD，连接AB交y轴于点F.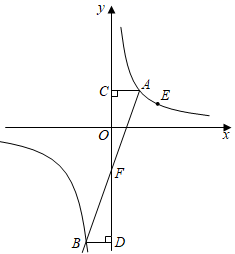

(1)、k＝；

(2)、设点A的横坐标为a，点F的纵坐标为m，求证：am＝﹣2；

(3)、连接CE，DE，当∠CED＝90°时，直接写出点A的坐标：.

查看试题解析
26. 如图1，正方形ABCD的边长为4，点P在边BC上，⊙O经过A，B，P三点.

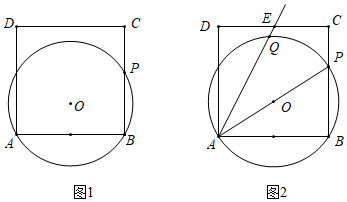(1)、若BP＝3，判断边CD所在直线与⊙O的位置关系，并说明理由；

(2)、如图2，E是CD的中点，⊙O交射线AE于点Q，当AP平分∠EAB时，求tan∠EAP的值.

查看试题解析
27. 将一张三角形纸片ABC放置在如图所示的平面直角坐标系中，点A(﹣6，0)，点B(0，2)，点C(﹣4，8)，二次函数y＝ax²+bx+c（a≠0）的图象经过点A，B，该抛物线的对称轴经过点C，顶点为D.

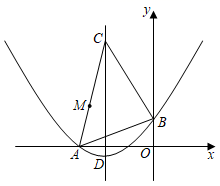(1)、求该二次函数的表达式及点D的坐标；

(2)、点M在边AC上（异于点A，C），将三角形纸片ABC折叠，使得点A落在直线AB上，且点M落在边BC上，点M的对应点记为点N，折痕所在直线l交抛物线的对称轴于点P，然后将纸片展开.
①请作出图中点M的对应点N和折痕所在直线l；（要求：尺规作图，不写作法，保留作图痕迹）

②连接MP，NP，在下列选项中：A.折痕与AB垂直，B.折痕与MN的交点可以落在抛物线的对称轴上，C. $\frac{M N}{M P}$ ＝ $\frac{3}{2}$ ，D. $\frac{M N}{M P}$ ＝ $\sqrt{2}$ ，所有正确选项的序号是 .

③点Q在二次函数y＝ax²+bx+c（a≠0）的图象上，当 $△$ PDQ∼ $△$ PMN时，求点Q的坐标.

查看试题解析
28. 如图1，∠A＝∠B＝∠C＝∠D＝∠E＝∠F＝90°，AB，FE，DC为铅直方向的边，AF，ED，BC为水平方向的边，点E在AB，CD之间，且在AF，BC之间，我们称这样的图形为“L图形”，记作“L图形ABC﹣DEF”.若直线将L图形分成面积相等的两个图形，则称这样的直线为该L图形的面积平分线.

(1)、【活动】
小华同学给出了图1的面积平分线的一个作图方案：如图2，将这个L图形分成矩形AGEF、矩形GBCD，这两个矩形的对称中心O₁ ， O₂所在直线是该L图形的面积平分线.请用无刻度的直尺在图1中作出其他的面积平分线.（作出一种即可，不写作法，保留作图痕迹）

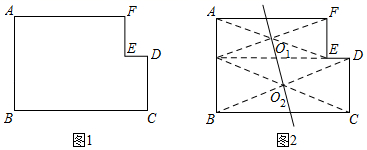(2)、【思考】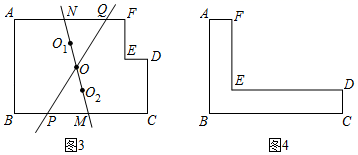

如图3，直线O₁O₂是小华作的面积平分线，它与边BC，AF分别交于点M，N，过MN的中点O的直线分别交边BC，AF于点P，Q，直线PQ（填“是”或“不是”）L图形ABCDEF的面积平分线.

(3)、【应用】
在L图形ABCDEF形中，已知AB＝4，BC＝6.

如图4，CD＝AF＝1.

①该L图形的面积平分线与两条水平的边分别相交于点P，Q，求PQ长的最大值；

②该L图形的面积平分线与边AB，CD分别相交于点G，H，当GH的长取最小值时，BG的长为 ▲ .

(4)、设 $\frac{C D}{A F}$ ＝t（t＞0），在所有的与铅直方向的两条边相交的面积平分线中，如果只有与边AB，CD相交的面积平分线，直接写出t的取值范围.

查看试题解析