江苏省淮安市2021年中考数学试卷
试卷更新日期:2021-09-06 类型:中考真卷
一、单选题
-
1. -5的绝对值等于( )A、-5 B、5 C、 D、2. 第七次全国人口普查结果显示,我国人口受教育水平明显提高,具有大学文化程度的人数约为218360000,将218360000用科学记数法表示为( )A、0.21836×109 B、2.1386×107 C、21.836×107 D、2.1836×1083. 计算(x5)2的结果是( )A、x3 B、x7 C、x10 D、x254. 如图所示的几何体的俯视图是( )
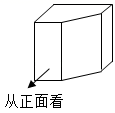 A、
A、 B、
B、 C、
C、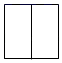 D、
D、 5. 下列事件是必然事件的是( )A、没有水分,种子发芽 B、如果a、b都是实数,那么a+b=b+a C、打开电视,正在播广告 D、抛掷一枚质地均匀的硬币,正面向上6. 如图,直线a、b被直线c所截,若a∥b,∠1=70°,则∠2的度数是( )
5. 下列事件是必然事件的是( )A、没有水分,种子发芽 B、如果a、b都是实数,那么a+b=b+a C、打开电视,正在播广告 D、抛掷一枚质地均匀的硬币,正面向上6. 如图,直线a、b被直线c所截,若a∥b,∠1=70°,则∠2的度数是( )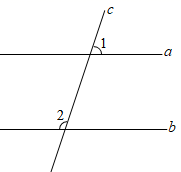 A、70° B、90° C、100° D、110°7. 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A、70° B、90° C、100° D、110°7. 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )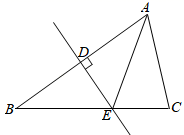 A、2 B、4 C、6 D、88. 《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的 ,则甲有50钱,乙若得到甲所有钱的 ,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )A、 B、 C、 D、
A、2 B、4 C、6 D、88. 《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的 ,则甲有50钱,乙若得到甲所有钱的 ,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )A、 B、 C、 D、二、填空题
-
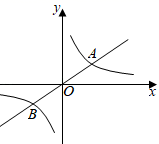
9. 分解因式: = .10. 现有一组数据4、5、5、6、5、7,这组数据的众数是.11. 分式方程 =1的解是.12. 若圆锥的侧面积为18π,底面半径为3,则该圆锥的母线长是.13. 一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是.14. 如图,正比例函数y=k1x和反比例函数y= 图象相交于A、B两点,若点A的坐标是(3,2),则点B的坐标是.
 15. 如图,AB是⊙O的直径,CD是⊙O的弦,∠CAB=55°,则∠D的度数是.
15. 如图,AB是⊙O的直径,CD是⊙O的弦,∠CAB=55°,则∠D的度数是.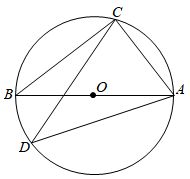 16. 如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是.
16. 如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是.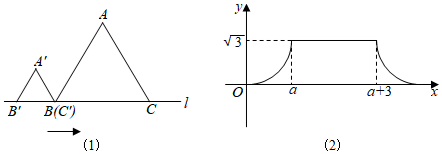
三、解答题
-
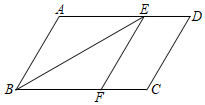
17.(1)、计算: ﹣(π﹣1)0﹣sin30°;(2)、解不等式组: .18. 先化简,再求值:( +1)÷ ,其中a=﹣4.19. 已知:如图,在▱ABCD中,点E、F分别在AD、BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
 20. 市环保部门为了解城区某一天18:00时噪声污染情况,随机抽取了城区部分噪声测量点这一时刻的测量数据进行统计,把所抽取的测量数据分成A、B、C、D、E五组,并将统计结果绘制了两幅不完整的统计图表.
20. 市环保部门为了解城区某一天18:00时噪声污染情况,随机抽取了城区部分噪声测量点这一时刻的测量数据进行统计,把所抽取的测量数据分成A、B、C、D、E五组,并将统计结果绘制了两幅不完整的统计图表.组别
噪声声级x/dB
频数
A
55≤x<60
4
B
60≤x<65
10
C
65≤x<70
m
D
70≤x<75
8
E
75≤x<80
n
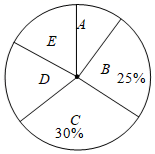
请解答下列问题:
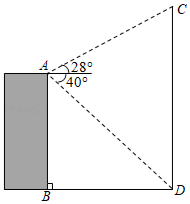
(1)、m= , n=;(2)、在扇形统计图中D组对应的扇形圆心角的度数是°;(3)、若该市城区共有400个噪声测量点,请估计该市城区这一天18:00时噪声声级低于70dB的测量点的个数.21. 在三张形状、大小、质地均相同的卡片上各写一个数字,分别为1、2、﹣1,现将三张卡片放入一只不透明的盒子中,搅匀后任意抽出一张,记下数字后放回,搅匀后再任意抽出一张记下数字.(1)、第一次抽到写有负数的卡片的概率是;(2)、用画树状图或列表等方法求两次抽出的卡片上数字都为正数的概率.22. 如图,平地上一幢建筑物AB与铁塔CD相距50m,在建筑物的顶部A处测得铁塔顶部C的仰角为28°、铁塔底部D的俯角为40°,求铁塔CD的高度.(参考数据:sin28°≈0.47,cos28°≈0.8,tan28°≈0.53,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
 23. 如图,方格纸上每个小正方形的边长均为1个单位长度,△ABC的顶点A、B、C都在格点上(两条网格线的交点叫格点).请仅用无刻度的直尺按下列要求画图,并保留画图痕迹(不要求写画法).
23. 如图,方格纸上每个小正方形的边长均为1个单位长度,△ABC的顶点A、B、C都在格点上(两条网格线的交点叫格点).请仅用无刻度的直尺按下列要求画图,并保留画图痕迹(不要求写画法).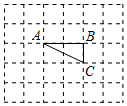 (1)、将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B1,点C的对应点为C1 , 画出△AB1C1;(2)、连接CC1 , △ACC1的面积为;(3)、在线段CC1上画一点D,使得△ACD的面积是△ACC1面积的 .24. 如图,在Rt△ABC中,∠ACB=90°,点E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)、将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B1,点C的对应点为C1 , 画出△AB1C1;(2)、连接CC1 , △ACC1的面积为;(3)、在线段CC1上画一点D,使得△ACD的面积是△ACC1面积的 .24. 如图,在Rt△ABC中,∠ACB=90°,点E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE. (1)、判断直线DE与⊙O的位置关系,并说明理由;(2)、若CD=3,DE= ,求⊙O的直径.25. 某超市经销一种商品,每件成本为50元.经市场调研,当该商品每件的销售价为60元时,每个月可销售300件,若每件的销售价每增加1元,则每个月的销售量将减少10件.设该商品每件的销售价为x元,每个月的销售量为y件.(1)、求y与x的函数表达式;(2)、当该商品每件的销售价为多少元时,每个月的销售利润最大?最大利润是多少?26. (知识再现)
(1)、判断直线DE与⊙O的位置关系,并说明理由;(2)、若CD=3,DE= ,求⊙O的直径.25. 某超市经销一种商品,每件成本为50元.经市场调研,当该商品每件的销售价为60元时,每个月可销售300件,若每件的销售价每增加1元,则每个月的销售量将减少10件.设该商品每件的销售价为x元,每个月的销售量为y件.(1)、求y与x的函数表达式;(2)、当该商品每件的销售价为多少元时,每个月的销售利润最大?最大利润是多少?26. (知识再现)学完《全等三角形》一章后,我们知道“斜边和一条直角边分别相等的两个直角三角形全等(简称HL定理)”是判定直角三角形全等的特有方法.
 (1)、(简单应用)
(1)、(简单应用)如图(1),在△ABC中,∠BAC=90°,AB=AC,点D、E分别在边AC、AB上.若CE=BD,则线段AE和线段AD的数量关系是.
(2)、(拓展延伸)在△ABC中,∠BAC= (90°< <180°),AB=AC=m,点D在边AC上.
若点E在边AB上,且CE=BD,如图(2)所示,则线段AE与线段AD相等吗?如果相等,请给出证明;如果不相等,请说明理由.
(3)、若点E在BA的延长线上,且CE=BD.试探究线段AE与线段AD的数量关系(用含有a、m的式子表示),并说明理由.27. 如图,在平面直角坐标系中,二次函数y= x2+bx+c的图象与x轴交于点A(﹣3,0)和点B(5,0),顶点为点D,动点M、Q在x轴上(点M在点Q的左侧),在x轴下方作矩形MNPQ,其中MQ=3,MN=2.矩形MNPQ沿x轴以每秒1个单位长度的速度向右匀速运动,运动开始时,点M的坐标为(﹣6,0),当点M与点B重合时停止运动,设运动的时间为t秒(t>0).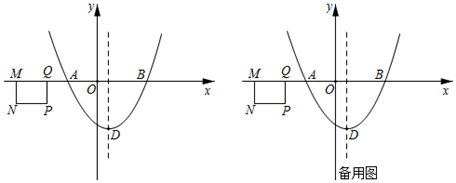 (1)、b= , c=.(2)、连接BD,求直线BD的函数表达式.(3)、在矩形MNPQ运动的过程中,MN所在直线与该二次函数的图象交于点G,PQ所在直线与直线BD交于点H,是否存在某一时刻,使得以G、M、H、Q为顶点的四边形是面积小于10的平行四边形?若存在,求出t的值;若不存在,请说明理由.(4)、连接PD,过点P作PD的垂线交y轴于点R,直接写出在矩形MNPQ整个运动过程中点R运动的路径长.
(1)、b= , c=.(2)、连接BD,求直线BD的函数表达式.(3)、在矩形MNPQ运动的过程中,MN所在直线与该二次函数的图象交于点G,PQ所在直线与直线BD交于点H,是否存在某一时刻,使得以G、M、H、Q为顶点的四边形是面积小于10的平行四边形?若存在,求出t的值;若不存在,请说明理由.(4)、连接PD,过点P作PD的垂线交y轴于点R,直接写出在矩形MNPQ整个运动过程中点R运动的路径长.