初中数学浙教版九年级上册3.6圆内接四边形同步练习
试卷更新日期：2021-09-06 类型：同步测试
一、单选题
-
1. 如图，已知四边形ABCD内接于⊙O，∠ABC=70°，则∠ADC的度数是（ ）
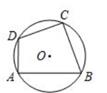A、70° B、110° C、130° D、140°2. 如图，四边形ABCD是 的内接四边形，若 ，则 等于（ ）
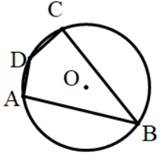A、 B、 C、 D、3. 在内接四边形 中， 只可能是下列四个选项中的（ ）A、 B、 C、 D、4. 如图，已知 是半圆 的直径， ， 是 的中点，那么 的度数是（ ）
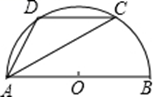A、 B、 C、 D、5. 如图，点 都是 上的点， ，则 （ ）
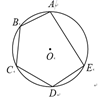A、 B、 C、 D、6. 如图，四边形ABCD是圆内接四边形，E是BC延长线上一点，若∠BAD＝105°，则∠DCE的大小是（ ）
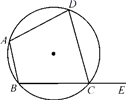A、115° B、105° C、100° D、95°7. 如图，点C在 上，点D在半径OA上，则下列结论正确的是（ ）
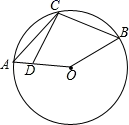A、∠DCB+ ∠O=180° B、∠ACB+ ∠O=180° C、∠ACB+∠O=180° D、∠CAO+∠CBO=180°8. 如图，四边形ABCD是⊙O的内接四边形，AB＝AD，若∠C＝68°，则∠ABD的度数为（ ）
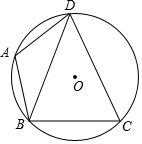A、34° B、56° C、68° D、112°9. 如图，有一圆内接正八边形 ABCDEFGH，若△ADE的面积为10，则正八边形 ABCDEFGH的面积为（ ）
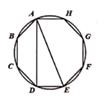A、40 B、50 C、60 D、8010. 如图，四边形ABCD内接于⊙O，DA=DC，∠CBE=50°，则∠DAC的大小为（ ）
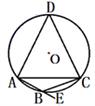A、130° B、100° C、65° D、50°二、填空题
-
11. 圆内接四边形ABCD中，∠A：∠B：∠C＝1：2：4，则∠D＝度．12. 已知点A、B、C、D均在圆上，AD∥BC，AC 平分∠BCD，∠ADC=120°，四边形的周长为10cm．，则∠ABC的度数为 ．
13. 如图，在圆内接四边形ABCD中， 、 、 的度数之比为 ，则 .
14. 如图，四边形ABCD为⊙O的内接四边形，已知∠A∶∠B∶∠C∶∠D=7∶9∶11∶9，则∠C= ．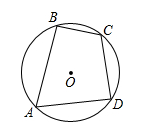
15. 如图，在⊙O的内接四边形ABCD中，AB＝AD，∠BCD＝140°.若点E在 上，则∠E＝°.
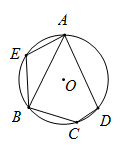16. 如图，四边形ABCD内接于圆O，AD∥BC，∠DAB=48°，则∠AOC的度数是.
三、解答题
-
17. 如图，四边形ABCD是⊙O的内接四边形，若∠BOD=88°，求∠BCD的度数．
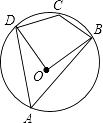18.如图，已知A、B、C、D是⊙O上的四点，延长DC，AB相交于点E，若DA=DE，求证：△BCE是等腰三角形．
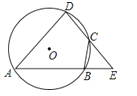19.如图，四边形ABCD内接于⊙O，∠ABC=130°，求∠OAC的度数．
20.如图，已知四边形ABCD内接于圆，对角线AC与BD相交于点E，F在AC上，AB=AD，∠BFC=∠BAD=2∠DFC．
（1）若∠DFC=40°，求∠CBF的度数；
（2）求证：CD⊥DF．
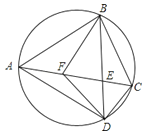21.如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E，F．
（1）若∠E+∠F=α，求∠A的度数（用含α的式子表示）；
（2）若∠E+∠F=60°，求∠A的度数．
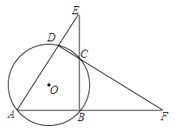
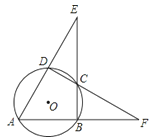22.如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．
（1）当∠E=∠F时，求∠ADC的度数；
（2）当∠A=55°，∠E=30°时，求∠F的度数；
（3）若∠E=α，∠F=β，且α≠β．请你用含有α、β的代数式表示∠A的大小．
23.如图，正三角形的边长为6cm，剪去三个角后成一个正六边形．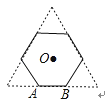
(1)、求这个正六边形的边长(2)、求这个正六边形的边心距(3)、设这个正六边形的中心为O，一边为AB，则AB绕点O旋转一周所得的图形是怎样的？（作图表示出来）并求出这条线段AB划过的面积．24.同圆或等圆中，圆心角互余的两个扇形叫做互余共轭扇形．如图⊙O内接八边形中，已知AB=BC=CD=DE=2，EF=FG=GH=HA=2 ．
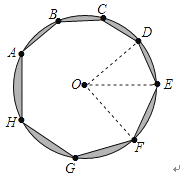(1)、扇形DOE与扇形EOF是否互余共轭扇形？请推理说明(2)、求⊙O的半径(3)、求阴影部分的面积．25.如图，圆心角120°的扇形OMN，绕着正六边形ABCDEF的中心O旋转，OM交AB于H，ON交CD于K，OM＞OA．
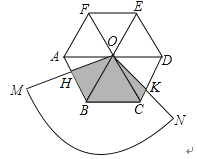(1)、证明：△AOH≌△COK(2)、若AB=2，求正六边形ABCDEF与扇形OMN重叠部分的面积．四、综合题
-
26. 综合题：(1)、已知：如图1，四边形ABCD内接于⊙O，延长BC至E．求证：∠A+∠BCD=180°，∠DCE=∠A．
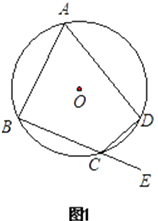(2)、依已知条件和（1）中的结论：①如图2，若点C在⊙O外，且A、C两点分别在直线BD的两侧．试确定∠A+∠BCD与180°的大小关系；
②如图3，若点C在⊙O内，且A、C两点分别在直线BD的两侧．试确定∠A+∠BCD与180°的大小关系．
