湖南省娄底市2020-2021学年高二上学期数学期中考试试卷
试卷更新日期:2021-09-06 类型:期中考试
一、单选题
-
1. 已知全集 ,集合 ,则 为( )A、 B、 C、 D、2. 2018°是( )A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角3. 在新高考改革中,一名高一学生在确定选修物理的情况下,想从政治,地理,生物,化学中再选两科学习,则所选两科中一定有地理的概率是( )A、 B、 C、 D、4. 已知椭圆 的焦点在y轴上,长轴长是短轴长的两倍,则 ( )A、 B、2 C、 D、45. 设向量 , ,且 ,则 ( )A、1 B、2 C、-1 D、-26. 设 ,则 的大小关系为( )A、 B、 C、 D、7. 已知函数=ax , =xa ,=logax(其中 且 ),在同一坐标系中画出其中两个函数在第一象限内的大致图像,其中正确的是( )A、
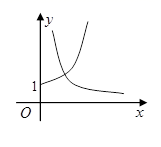 B、
B、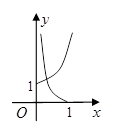 C、
C、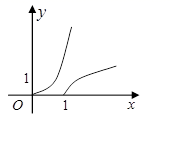 D、
D、 8. 在数列 中,已知 , , ,则 等于( )A、 B、 C、 D、
8. 在数列 中,已知 , , ,则 等于( )A、 B、 C、 D、二、多选题
-
9. 给出下列四个关系式,其中不正确的是( ).A、 B、 C、 D、10. 设 , , ,以下四个命题中正确的是( ).A、若 为定值 ,则 有最大值 B、若 ,则 有最大值4 C、若 ,则 有最小值4 D、若 总成立,则 的取值范围为11. 已知双曲线C的标准方程为 ,则( )A、双曲线C的离心率等于半焦距 B、双曲线 与双曲线C有相同的渐近线 C、双曲线C的一条渐近线被圆 截得的弦长为 D、直线 与双曲线C的公共点个数只可能为0,1,212. 如图,正方体 的棱长为1,线段 上有两个动点E、F,且 ,则下列结论中正确的是( )
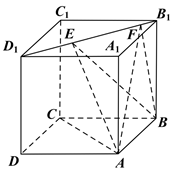 A、线段 上存在点E、F使得 B、 平面ABCD C、 的面积与 的面积相等 D、三棱锥A-BEF的体积为定值
A、线段 上存在点E、F使得 B、 平面ABCD C、 的面积与 的面积相等 D、三棱锥A-BEF的体积为定值三、填空题
-
13. 已知p:“ ”,q:“x=4”,则p是q的条件.14. 双曲线 的渐近线方程为.15. 若 , ,则函数 有零点的概率为.16. 已知数列 的前n项和Sn=2an-1(n∈N*),设bn=1+log2an , 则数列 的前n项和Tn= .
四、解答题
-
17. 已知向量 .记 .(1)、求 的最小正周期及单调增区间;(2)、在 中,角 的对边分别为 若 ,求 的值.18. 在① ,② ,③ 三个条件中任选一个,补充在下面的问题中,并解答.
设 是公比大于0的等比数列,其前n项和为 是等差数列.已知 , ,__________.
(1)、求 和 的通项公式;(2)、设 求 .19. 如图已知四棱锥A-BCC1B1底面为矩形,侧面ABC为等边三角形,且矩形BCC1B1与三角形ABC所在的平面互相垂直,BC=4,BB1=2,D为AC的中点.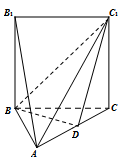 (1)、求证: 平面 ;(2)、求点D到平面ABC1的距离.
(1)、求证: 平面 ;(2)、求点D到平面ABC1的距离.