初中数学浙教版九年级上册3.5 圆周角同步练习
试卷更新日期：2021-09-06 类型：同步测试
一、单选题
-
1. 如图，AB是 的直径，点C，D在 上， ，则 的大小是（ ）
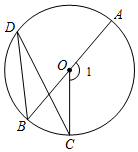A、 B、 C、 D、2. 如图，A ， B ， C是⊙O上的三点，若 ，则 的度数是（ ）
A、40° B、35° C、30° D、25°3. 如图，点A ， B ， C为⊙O上的三点，∠AOB ∠BOC ， ∠BAC＝30°，则∠AOC的度数为（ ）
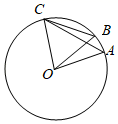A、100° B、90° C、80° D、60°4. 如图，A，B，C是半径为1的⊙O上的三个点，若AB＝ ，∠CAB＝30°，则∠ABC的度数为（ ）
A、95° B、100° C、105° D、110°5. 如图，已知 为 的直径，点C在 上， ，则 的度数为（ ）
A、 B、 C、 D、6. 如图，AB是⊙O的直径，C，D两点在⊙O上，若∠C＝40°，则∠ABD的度数为（ ）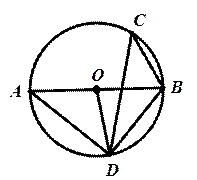
A、40° B、50° C、80° D、90°7. 如图，AB为⊙O的直径，C，D为⊙O上的点， ＝ .若∠CBA＝40°，则∠CBD的大小为（ ）
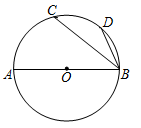A、50° B、40° C、25° D、20°8. 如图， 为 的直径， 为 的弦，若 ，则 的度数为（ ）
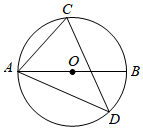A、 B、 C、 D、9. 如图， 是 的直径， 是 的切线， ， 交 于点 ， 是 上一点，延长 交 于点 ，则 的度数是（ ）
A、35° B、40° C、45° D、50°10. 如图，矩形 中， ， ．若 是矩形 边上一动点，且使得 ，则这样的点 有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图，D为⊙O上一点， ，∠AOB＝50°，则∠ADC的度数是.
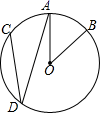12. 如图，AB是⊙O的直径，BC是⊙O的弦.若∠OBC＝60°，则∠BAC=.
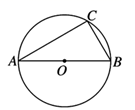13. 如图，点 ， ， 在 上， ，则 的度数为 ．
14. 如图， 是 的直径，点 在 上，若 ，则 °.
15. 如图， 为 的直径， 为 的弦， ，则 的度数为.
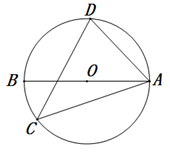16. 如图，等边 的三个顶点在圆 上， 是直径，则 度， 度， 度．
三、解答题
-
17. 如图， 为等边三角形，将 边绕点 顺时针旋转 ，得到线段 连接 ，求 的度数﹒
18. 如图所示，△ABC内接于⊙O，AB＝AC，D在 上，连接CD交AB于点E，B是 的中点，求证：∠B＝∠BEC.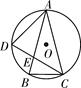
19. 如图，A ， D是半圆上的两点，O为圆心，BC是直径，∠D＝35°，求∠OAC的度数．
20. AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q.若AB=2，则线段BQ的长为多少？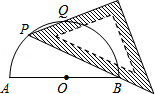
21. 如图所示，圆O为△ABC的外接圆，AM，AT分别为中线和角平分线，过点B和点C的圆O的切线相交于点P，连结AP，与BC和圆O分别相交于点D、E.
求证：点T是△AME的内心。
四、综合题
-
22. 如图， 是 直径， ， 是圆上点且在 同侧．
(1)、如果 ，则 °．(2)、如果 ， ，求 度数．23. 已知：如图△ABC内接于圆O，AB=AC，D为弧BC上任意一点，连结AD，BD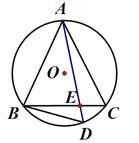
(1)、若∠ADB=65°，求∠BAC的度数(2)、求证：∠ABD=∠AEB24. 如图AB是半圆的直径，图1中，点C在半圆外；图2中，点C在半圆内，请仅用无刻度的直尺按要求画图．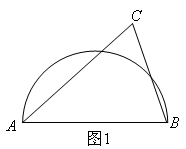
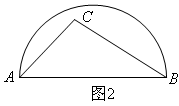(1)、在图1中，画出△ABC的三条高的交点；(2)、在图2中，画出△ABC中AB边上的高．25. 如图， 的直径AB的长为10，弦AC的长为 的平分线交 于点D．
(1)、求BC的长；(2)、求弦BD的长．26. 如图，已知AB、AD是⊙O的弦，点C是DO的延长线与弦AB的交点，∠ABO=30°，OB=2．
(1)、求弦AB的长；
(2)、若∠D=20°，求∠BOD的度数．27. 如图，AB是⊙O的直径，弦CD⊥AB于点E，点P⊙O上，∠1=∠C．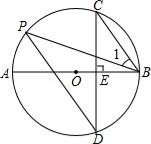
(1)、求证：CB∥PD；(2)、若∠ABC=55°，求∠P的度数．28. 已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D
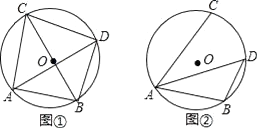(1)、如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；
(2)、如图②，若∠CAB=60°，求BD的长．29. 如图，在锐角△ABC中，AB＞AC，AD⊥BC于点D，以AD为直径的⊙O分别交AB，AC于点E，F，连接DE，DF.
(1)、求证：∠EAF＋∠EDF＝180°.(2)、已知P是射线DC上一个动点，当点P运动到PD＝BD时，连接AP，交⊙O于点G，连接DG.设∠EDG＝∠α，∠APB＝∠β，那么∠α与∠β有何数量关系？试证明你的结论(在探究∠α与∠β的数量关系时，必要时可直接运用(1)的结论进行推理与解答)．