初中数学浙教版九年级上册3.4 圆心角同步练习
试卷更新日期:2021-09-06 类型:同步测试
一、单选题
-
1. 如图, 是 的直径, , , 则 的度数是( ).
 A、52° B、57° C、66° D、78°2. 下列说法中,正确的是( )A、等弦所对的弧相等 B、在同圆或等圆中,相等的弧所对的弦相等 C、圆心角相等,所对的弦相等 D、弦相等所对的圆心角相等3. 如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB的度数是( )
A、52° B、57° C、66° D、78°2. 下列说法中,正确的是( )A、等弦所对的弧相等 B、在同圆或等圆中,相等的弧所对的弦相等 C、圆心角相等,所对的弦相等 D、弦相等所对的圆心角相等3. 如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB的度数是( )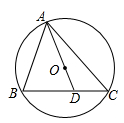 A、70° B、80° C、82° D、85°4. 下图中 是圆心角的是( )A、
A、70° B、80° C、82° D、85°4. 下图中 是圆心角的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图, 是 的直径, , 是 的两条弦, ,连接 ,若 ,则 的度数是( )
5. 如图, 是 的直径, , 是 的两条弦, ,连接 ,若 ,则 的度数是( ) A、10° B、20° C、30° D、40°6. 如图,在△ABC中,∠C=90°, 的度数为α , 以点C为圆心,BC长为半径的圆交AB于点D , 交AC于点E , 则∠A的度数为( )
A、10° B、20° C、30° D、40°6. 如图,在△ABC中,∠C=90°, 的度数为α , 以点C为圆心,BC长为半径的圆交AB于点D , 交AC于点E , 则∠A的度数为( ) A、45º- α B、 α C、45º+ α D、25º+ α7. 如图,点A,B,D在⊙O上,∠A=15°,BC是⊙O的切线,点B为切点,OD的延长线交BC于点C,若BC的长为2,则DC的长是( )
A、45º- α B、 α C、45º+ α D、25º+ α7. 如图,点A,B,D在⊙O上,∠A=15°,BC是⊙O的切线,点B为切点,OD的延长线交BC于点C,若BC的长为2,则DC的长是( ) A、1 B、4-2 C、2 D、4 -48. 如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )
A、1 B、4-2 C、2 D、4 -48. 如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )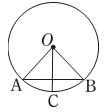 A、40° B、45° C、50° D、60°9. 如图, , 是 的直径, ,若 ,则 的度数是( )
A、40° B、45° C、50° D、60°9. 如图, , 是 的直径, ,若 ,则 的度数是( )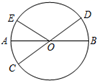 A、32° B、60° C、68° D、64°10. 如图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是( )
A、32° B、60° C、68° D、64°10. 如图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是( )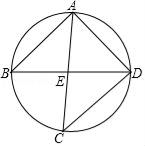 A、AB=AD B、BE=CD C、AC=BD D、BE=AD
A、AB=AD B、BE=CD C、AC=BD D、BE=AD二、填空题
-
11. 如图, , 是圆O的两条相等的弦,弧 ,弧 的度数分别为30度,120度,P为劣弧 上一点,则 °.
 12. 如图,在⊙O中, ,∠1=30°,则∠2=°.
12. 如图,在⊙O中, ,∠1=30°,则∠2=°.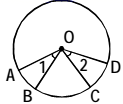 13. 如图,在⊙O中, ,AB=3,则AC=.
13. 如图,在⊙O中, ,AB=3,则AC=.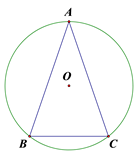 14. 将一个圆分割成3个扇形,使它们的圆心角的度数比为2:3:4,则这三个扇形的圆心角最小为。15. 已知AB、CD是⊙O的两条弦,若 ,且AB=2,则CD= .16. 如图,在⊙O中, ,若∠AOB=40°,则∠COD= .
14. 将一个圆分割成3个扇形,使它们的圆心角的度数比为2:3:4,则这三个扇形的圆心角最小为。15. 已知AB、CD是⊙O的两条弦,若 ,且AB=2,则CD= .16. 如图,在⊙O中, ,若∠AOB=40°,则∠COD= .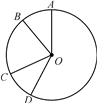 17. 如图的齿轮有30个齿,每两齿之间的间隔相等,则相邻两齿间的圆心角 等于度.
17. 如图的齿轮有30个齿,每两齿之间的间隔相等,则相邻两齿间的圆心角 等于度.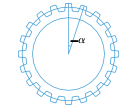
三、解答题
-
18. 已知:A、B、C、D是⊙O上的四个点,且 ,求证:AC=BD .
 19. 如图,正方形ABCD内接于⊙O,M为弧CD的中点,连接AM,BM,求证:AM=BM.
19. 如图,正方形ABCD内接于⊙O,M为弧CD的中点,连接AM,BM,求证:AM=BM. 20. 如图,点A,B,C,D在⊙O上,BD=AC.求证:AB=CD.
20. 如图,点A,B,C,D在⊙O上,BD=AC.求证:AB=CD. 21. 如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
21. 如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
 22. O为等腰△ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.求证:
22. O为等腰△ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.求证:(1)∠AOE=∠BOD;
(2)= .
四、综合题
-
23. 我们学习了“圆心角、弧、弦的关系”,实际上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”如下:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距(弦心距指从圆心到弦的距离,如图1中的OC、OC′,弦心距也可以说成圆心到弦的垂线段的长度)中有一组量相等,那么它们对应的其余各组量也相等.请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题:
如图2,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A、B、C、D.
 (1)、求证:AB=CD;(2)、若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.24.
(1)、求证:AB=CD;(2)、若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.24.O为等腰△ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.
 (1)、求证:∠AOE=∠BOD.
(1)、求证:∠AOE=∠BOD.
(2)、求证:




 与
与 的大小有什么关系?为什么?
的大小有什么关系?为什么? 