初中数学浙教版九年级上册3.3垂径定理 同步练习
试卷更新日期:2021-09-06 类型:同步测试
一、单选题
-
1. 如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP=2,则CD的长为( )
 A、 B、 C、 D、2. 如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5,则AB的长为( )
A、 B、 C、 D、2. 如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5,则AB的长为( ) A、8 B、12 C、16 D、23. 如图,AB为圆O的直径,C、D两点均在圆上,其中OD⊥AC交AC于E点.若DE=1,BC=6,则AC=( )
A、8 B、12 C、16 D、23. 如图,AB为圆O的直径,C、D两点均在圆上,其中OD⊥AC交AC于E点.若DE=1,BC=6,则AC=( ) A、3 B、 C、5 D、4. 已知,如图 的直径为 ,弦 垂直平分半径 ,则弦 的长为( )
A、3 B、 C、5 D、4. 已知,如图 的直径为 ,弦 垂直平分半径 ,则弦 的长为( ) A、 B、 C、 D、5. 下列说法正确的是( )A、垂直于弦的直线平分弦所对的两条弧 B、平分弦的直径垂直于弦 C、垂直于直径平分这条直径 D、弦的垂直平分线经过圆心6. 水平放置的圆柱形排水管道截面半径为1 m.若管道中积水最深处为0.4 m,则水面宽度为( )
A、 B、 C、 D、5. 下列说法正确的是( )A、垂直于弦的直线平分弦所对的两条弧 B、平分弦的直径垂直于弦 C、垂直于直径平分这条直径 D、弦的垂直平分线经过圆心6. 水平放置的圆柱形排水管道截面半径为1 m.若管道中积水最深处为0.4 m,则水面宽度为( ) A、0.8 m B、1.2 m C、1.6 m D、1.8 m7. 如图,⊙O的直径CD垂直弦AB于点E , 且CE=2,DE=8,则BE的长为( )
A、0.8 m B、1.2 m C、1.6 m D、1.8 m7. 如图,⊙O的直径CD垂直弦AB于点E , 且CE=2,DE=8,则BE的长为( ) A、2 B、4 C、6 D、88. 如图, 与 轴交于点 , ,圆心 的横坐标为 ,则 的半径为( )
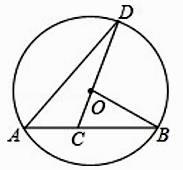
A、2 B、4 C、6 D、88. 如图, 与 轴交于点 , ,圆心 的横坐标为 ,则 的半径为( ) A、3 B、4 C、5 D、69. 如图, 是 的直径,弦 交 于点 , , , ,则 的长为( )
A、3 B、4 C、5 D、69. 如图, 是 的直径,弦 交 于点 , , , ,则 的长为( )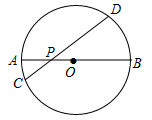 A、 B、 C、 D、1210. 《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为 1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )
A、 B、 C、 D、1210. 《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为 1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )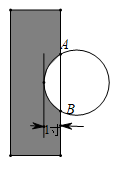 A、13 B、24 C、26 D、28
A、13 B、24 C、26 D、28二、填空题
-
11. 赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径=米.
 12. 如图,已知AB是半圆O的直径,弦CD∥AB , CD=8.AB=10,则CD与AB之间的距离是 .
12. 如图,已知AB是半圆O的直径,弦CD∥AB , CD=8.AB=10,则CD与AB之间的距离是 . 13. 如图,一个宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”,“8”(单位:cm),那么,该圆的半径为.
13. 如图,一个宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”,“8”(单位:cm),那么,该圆的半径为. 14. 如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D,且OD=DC,P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则S△PAB的最大值为.
14. 如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D,且OD=DC,P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则S△PAB的最大值为. 15. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的半径为cm.
15. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的半径为cm. 16. ⊙O半径为5,弦AB=6cm,CD=8cm,且AB∥CD.则AB与CD之间的距离 .
16. ⊙O半径为5,弦AB=6cm,CD=8cm,且AB∥CD.则AB与CD之间的距离 .三、解答题
-
17. ⊙O的半径为5cm,弦AB=6cm,CD=8cm,且AB∥CD,求两弦之间的距离.18. 如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
 19. 如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,求弦BD的长
19. 如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,求弦BD的长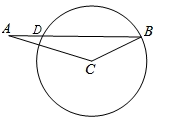 20. 已知:如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且OE=OF.求证:AE=BF.
20. 已知:如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且OE=OF.求证:AE=BF.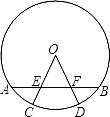
四、综合题
-
21. 如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D.
 (1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长
(1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长
22. 如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm, (1)、求⊙O的半径;(2)、求O到弦BC的距离.23. 一次函数 的图象与轴的负半轴相交于点 ,与 轴的正半轴相交于点 ,且 . 的外接圆的圆心 的横坐标为 .
(1)、求⊙O的半径;(2)、求O到弦BC的距离.23. 一次函数 的图象与轴的负半轴相交于点 ,与 轴的正半轴相交于点 ,且 . 的外接圆的圆心 的横坐标为 . (1)、求一次函数的解析式;(2)、求图中阴影部分的面积.24. 已知:如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E.
(1)、求一次函数的解析式;(2)、求图中阴影部分的面积.24. 已知:如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E. (1)、求证:∠CDB=∠A;(2)、若BD=5,AD=12,求CD的长.25. 好山好水好江山,石拱桥在江山处处可见,小明要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面宽度16m时,拱顶高出水平 面4m,货船宽12m,船舱顶部为矩形并高出水面3m。
(1)、求证:∠CDB=∠A;(2)、若BD=5,AD=12,求CD的长.25. 好山好水好江山,石拱桥在江山处处可见,小明要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面宽度16m时,拱顶高出水平 面4m,货船宽12m,船舱顶部为矩形并高出水面3m。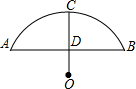 (1)、请你帮助小明求此圆弧形拱桥的半径。(2)、小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由。
(1)、请你帮助小明求此圆弧形拱桥的半径。(2)、小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由。