初中数学浙教版九年级上册3.2 图形的旋转同步练习
试卷更新日期:2021-09-06 类型:同步测试
一、单选题
-
1. 如图,在平面内将五角星绕其中心旋转180°后所得到的图案是( )
 A、
A、 B、
B、 C、
C、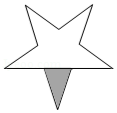 D、
D、 2. 在平面直角坐标系中,点A的坐标为(2,3),将点 绕原点逆时针旋转90°得到点 ,则点 的坐标为( )A、(-3,2) B、(3,-2) C、(3,2) D、(-2,-3)3. 如图,将 绕点O逆时针旋转60°后得到 ,若 , ,则 ( )
2. 在平面直角坐标系中,点A的坐标为(2,3),将点 绕原点逆时针旋转90°得到点 ,则点 的坐标为( )A、(-3,2) B、(3,-2) C、(3,2) D、(-2,-3)3. 如图,将 绕点O逆时针旋转60°后得到 ,若 , ,则 ( ) A、25° B、35° C、45° D、55°4. 如图,将 绕点 顺时针旋转得到 ,且点 恰好在 上, ,则 的度数是( )
A、25° B、35° C、45° D、55°4. 如图,将 绕点 顺时针旋转得到 ,且点 恰好在 上, ,则 的度数是( ) A、 B、 C、 D、5. 如图,△AOB中,OA=4,OB=6,AB=2 ,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )
A、 B、 C、 D、5. 如图,△AOB中,OA=4,OB=6,AB=2 ,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )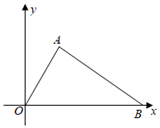 A、(4,2)或(﹣4,2) B、(2 ,﹣4)或(﹣2 ,4) C、(﹣2 ,2)或(2 ,﹣2) D、(2,﹣2 )或(﹣2,2 )6. 如图,将 绕着点 顺时针旋转,得到 (点 落在 外),若 , ,则旋转角度是( ).
A、(4,2)或(﹣4,2) B、(2 ,﹣4)或(﹣2 ,4) C、(﹣2 ,2)或(2 ,﹣2) D、(2,﹣2 )或(﹣2,2 )6. 如图,将 绕着点 顺时针旋转,得到 (点 落在 外),若 , ,则旋转角度是( ). A、20° B、30° C、40° D、50°7. 如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按逆时针方向旋转90°后,得到△A'B'C′,则点A′的坐标是( )
A、20° B、30° C、40° D、50°7. 如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按逆时针方向旋转90°后,得到△A'B'C′,则点A′的坐标是( ) A、(5,1) B、(5,﹣1) C、(﹣1,5) D、(1,﹣5)8. 如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD , 若 ,则∠ABE的度数为( )
A、(5,1) B、(5,﹣1) C、(﹣1,5) D、(1,﹣5)8. 如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD , 若 ,则∠ABE的度数为( ) A、25° B、30° C、35° D、40°9. 如图,在 ABC中,∠CAB=70°,将 ABC绕点A逆时针旋转到 的位置,使得 ∥AB , 则 的度数是( )
A、25° B、30° C、35° D、40°9. 如图,在 ABC中,∠CAB=70°,将 ABC绕点A逆时针旋转到 的位置,使得 ∥AB , 则 的度数是( ) A、70° B、35° C、40° D、50°10. 如图,将 纸片绕点C顺时针旋转 得到 ,连接 ,若 ,则 的度数为( )
A、70° B、35° C、40° D、50°10. 如图,将 纸片绕点C顺时针旋转 得到 ,连接 ,若 ,则 的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,△ABC绕点A按逆时针方向旋转50°后的图形为△AB1C1 , 则∠ABB1= .
 12. 如图,在平面直角坐标系中,每个小正方形边长均为1,将 ABC绕P点逆时针旋转至 ,使点B′恰好落在y轴上,则旋转中心P的坐标是.
12. 如图,在平面直角坐标系中,每个小正方形边长均为1,将 ABC绕P点逆时针旋转至 ,使点B′恰好落在y轴上,则旋转中心P的坐标是. 13. 如图,在方格纸上建立的平面直角坐标系中,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△FEC , 则点A的对应点F的坐标是 .
13. 如图,在方格纸上建立的平面直角坐标系中,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△FEC , 则点A的对应点F的坐标是 . 14. 如图,在平面直角坐标系中, 的直角顶点C的坐标为 ,点A在x轴正半轴上,且 .将 绕点C逆时针旋转 ,则旋转后点A的对应点的坐标为 .
14. 如图,在平面直角坐标系中, 的直角顶点C的坐标为 ,点A在x轴正半轴上,且 .将 绕点C逆时针旋转 ,则旋转后点A的对应点的坐标为 .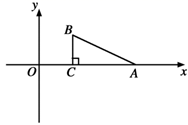 15. 如图,将Rt△ABC(∠BAC=65°)绕点A顺时针旋转到△AB1C1的位置,使得点C,A,B1在同一直线上,则旋转角度为.
15. 如图,将Rt△ABC(∠BAC=65°)绕点A顺时针旋转到△AB1C1的位置,使得点C,A,B1在同一直线上,则旋转角度为. 16. 如图,在凸四边形 中, , ,则线段 的长等于 .
16. 如图,在凸四边形 中, , ,则线段 的长等于 .
三、解答题
-
17. 如图,将 以点 为旋转中心,顺时针旋转 ,得到 ,过点 作 ,交 的延长线于点 ,求证: .
 18. 如图
18. 如图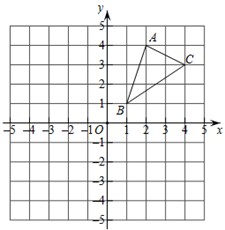
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)写出A2 和C2两点坐标.19. 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形.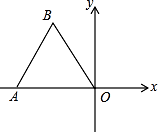 (1)、写出△OAB各顶点的坐标;(2)、以点O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,写出A′,B′的坐标.
(1)、写出△OAB各顶点的坐标;(2)、以点O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,写出A′,B′的坐标.
20. 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2 . (1)、在网格中画出△A1B1C1;(2)、在网格中画出A1B2C2 .21.
(1)、在网格中画出△A1B1C1;(2)、在网格中画出A1B2C2 .21.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(Ⅰ)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(Ⅱ)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.

四、综合题
-
22. 如图,在8×8的方格纸中,每个小方格的顶点称为格点,请按要求画格点四边形ABCD .
 (1)、在图1中画平行四边形ABCD , 使点P是它的对称中心.(2)、在图2中画四边形ABCD , 使得∠D=90°,且PB∥CD .23. 如图1,把△ABC沿直线BC平移线段BC的长度,得到△ECD;如图2,以BC为轴,把△ABC沿BC翻折180°,可以得到△DBC;如图3,以点A为中心,把△ABC旋转180°,可以得到△AED . 像这样,其中一个三角形是由另一个三角形按平移、翻折、旋转等方法得到的,这种只改变位置,不改变形状、大小的图形变换,叫做三角形的全等变换.回答下列问题:
(1)、在图1中画平行四边形ABCD , 使点P是它的对称中心.(2)、在图2中画四边形ABCD , 使得∠D=90°,且PB∥CD .23. 如图1,把△ABC沿直线BC平移线段BC的长度,得到△ECD;如图2,以BC为轴,把△ABC沿BC翻折180°,可以得到△DBC;如图3,以点A为中心,把△ABC旋转180°,可以得到△AED . 像这样,其中一个三角形是由另一个三角形按平移、翻折、旋转等方法得到的,这种只改变位置,不改变形状、大小的图形变换,叫做三角形的全等变换.回答下列问题: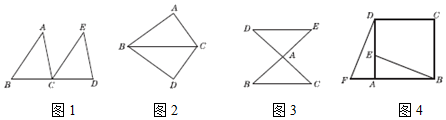 (1)、在图4中,可以使△ABE通过平移、翻折、旋转中的哪一种方法得到△ADF?(2)、图中线段BE与DF相等吗?为什么?24. 如图,在等腰 中,AC=AB,∠CAB=90°,E是BC上一点,将E点绕A点逆时针旋转90°到AD,连接DE、CD.
(1)、在图4中,可以使△ABE通过平移、翻折、旋转中的哪一种方法得到△ADF?(2)、图中线段BE与DF相等吗?为什么?24. 如图,在等腰 中,AC=AB,∠CAB=90°,E是BC上一点,将E点绕A点逆时针旋转90°到AD,连接DE、CD. (1)、求证: ;(2)、当BC=6,CE=2时,求DE的长.25. 如图,点E为正方形ABCD的边AB上一点,AB=12,AE=5,将△DAE旋转后能与△DCF重合。
(1)、求证: ;(2)、当BC=6,CE=2时,求DE的长.25. 如图,点E为正方形ABCD的边AB上一点,AB=12,AE=5,将△DAE旋转后能与△DCF重合。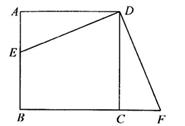 (1)、旋转中心是哪一点?(2)、旋转的最小角是多少度?(3)、求四边形DEBF的周长和面积。26. 如图
(1)、旋转中心是哪一点?(2)、旋转的最小角是多少度?(3)、求四边形DEBF的周长和面积。26. 如图
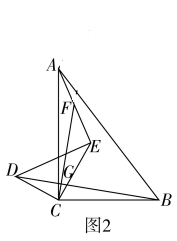 (1)、如图1.在Rt△ACB中,∠ACB=90°,AC=8,BC=6,点D、E分别在边CA,CB上且CD=3,CE=4,连接AE,BD,F为AE的中点,连接CF交BD于点G,则线段CG所在直线与线段BD所在直线的位置关系是.(提示:延长CF到点M,使FM=CF,连接AM)(2)、将△DCE绕点C逆时针旋转至图2所示位置时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)、将△DCE绕点C逆时针在平面内旋转,在旋转过程中,当B,D,E三点在同一条直线上时,CF的长为.27. 操作与探索:
(1)、如图1.在Rt△ACB中,∠ACB=90°,AC=8,BC=6,点D、E分别在边CA,CB上且CD=3,CE=4,连接AE,BD,F为AE的中点,连接CF交BD于点G,则线段CG所在直线与线段BD所在直线的位置关系是.(提示:延长CF到点M,使FM=CF,连接AM)(2)、将△DCE绕点C逆时针旋转至图2所示位置时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)、将△DCE绕点C逆时针在平面内旋转,在旋转过程中,当B,D,E三点在同一条直线上时,CF的长为.27. 操作与探索:已知点O为直线AB上一点,作射线OC,将直角三角板ODE放置在直线上方(如图①),使直角顶点与点O重合,一条直角边OD重叠在射线OA上,将三角板绕点O旋转.
 (1)、当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC;(2)、若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角;(3)、若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
(1)、当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC;(2)、若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角;(3)、若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.