初中数学浙教版八年级上册第5章 一次函数单元检测

试卷更新日期：2021-09-06 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 2018年10月，历时九年建设的港珠澳大桥正式通车，住在珠海的小亮一家，决定自驾去香港旅游，经港珠澳大桥去香港全程108千米，汽车行进速度v为110千米/时，若用s (千米)表示小亮家汽车行驶的路程，行驶时间用t (小时)表示，下列说法正确的是（    ）
    A、s是自变量， t是因变量 B、s是自变量， v是因变量 C、t是自变量， s是因变量 D、v是自变量， t是因变量

    查看试题解析

  • 2. 在函数 y=−2x−5 中， b 的值为（    ）
    A、-5 B、2 C、5 D、-2

    查看试题解析

  • 3. 下列各曲线表示y是x的函数的是（    ）

    A、① B、①② C、①②③ D、①②③④

    查看试题解析

  • 4. 某商城进一批苹果，在6月27日按照早中晚三个批次销售，销售情况如表，在该变化过程中，常量是（     ）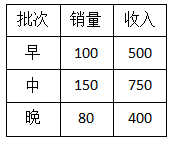

    A、批次 B、销售量 C、收入 D、单价

    查看试题解析

  • 5. 已知y是x的正比例函数，且函数图象经过点 (4 ， −6) ，则在此正比例函数图象上的点是（   ）
    A、(2 ， 3) B、(−6 ， 4) C、(3 ， −2) D、(−4 ， 6)

    查看试题解析

  • 6. 对于一次函数 y=kx+b （ k ， b 为常数，且 k≠0 ）表中给出5组自变量及其对应的函数值，其中只有1个函数值计算有误，则这个错误的函数值是（   ）

    x

    …

    −1

    0

    1

    2

    3

    …

    y

    …

    −2

    1

    4

    8

    10

    …
    A、1 B、4 C、8 D、10

    查看试题解析

  • 7. 已知点（﹣1，y1）、（3，y2）在一次函数y＝﹣x＋2的图象上，则y1、y2、0的大小关系是（    ）
    A、0＜y1＜y2 B、y1＜0＜y2 C、y1＜y2＜0 D、y2＜0＜y1

    查看试题解析

  • 8. 将直线y＝4x＋3向下平移5个单位后，所得直线的表达式是（   ）
    A、y＝4（x＋5）x＋3 B、y＝4（x﹣5）x＋3 C、y＝4x＋8 D、y＝4x﹣2

    查看试题解析

  • 9. 如图，正比例函数 y=kx （ k ≠0）和一次函数 y=ax+b （ a ≠0）的图象相交于点A（1，1），则不等式 kx≥ax+b 的解集是（   ）

    A、x ≤1 B、x≥1 C、x ＜1 D、x ＞1

    查看试题解析

  • 10. 如图，设甲、乙两车在同一直线公路上匀速行驶，开始甲车在乙车的前面，当乙车追上甲车后，两车停下来，把乙车的货物转给甲车，然后甲车继续前行，乙车原地返回．设x小时后两车间的距离为y千米，y关于x的函数关系如图所示，则乙车的速度为（    ）

    A、50千米/小时 B、45千米/小时 C、40千米/小时 D、35千米/小时

    查看试题解析

二、填空题

  • 11. 我们知道，地面有一定的温度，高空也有一定的温度，且高空中的温度是随着距地面高度的变化而变化的，如果表示 t 某高空中的温度， h 表示距地面的高度，则是自变量.

    查看试题解析

  • 12. 一列慢车从 A 地驶往 B 地，一列快车从 B 地驶往 A 地.两车同时出发，各自抵达目的地后停止，如图所示，折线表示两车之间的距离 y （km）与慢车行驶时间 t （h）之间的关系.当快车到达 A 地时，慢车与 B 地的距离为km.

    查看试题解析

  • 13. 甲、乙两人同时从 A 、 B 两地出发相向而行，甲先步行到达 B 地后原地休息，甲、乙两人的距离 y(km) 与乙步行的时间 x(h) 之间的函数关系的图象如图，则步行全程甲比乙少用小时.

    查看试题解析

  • 14. 将直线 y=3x−1 向上平移两个单位长度后，得到的直线解析式是

    查看试题解析

  • 15. 某函数的图象经过（1， −1 ），且函数y的值随自变量x的值增大而增大．请你写出一个符合上述条件的函数关系式： ．

    查看试题解析

  • 16. 小球从离地面为h（单位：m）的高处自由下落，落到地面所用时间为t（单位：s），经过实验，发现h与 t2 成正比例关系，当 h=20 时， t=2 ，则当 h=10 时，t的值是 ．

    查看试题解析

三、解答题

  • 17.

    下表给出了橘农王林去年橘子的销售额（元）随橘子卖出质量（千克）的变化的有关数据：

    （1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？

    （2）当橘子卖出5千克时，销售额是多少？

    （3）估计当橘子卖出50千克时，销售额是多少？

    查看试题解析

  • 18. 求下列函数中自变量的取值范围．

    ①y= −52x−1 ②y= 2x−1 ．

    查看试题解析

  • 19. 如图，已知直线l1经过点A（0，-1）与点P（2，3），另一条直线l2经过点P，且与y轴交于点B（0，m）．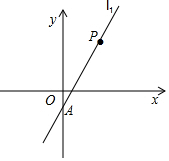

    (1)、求直线l1的解析式；
    (2)、若△APB的面积为3，求m的值．

    查看试题解析

  • 20. 如图，直线 l1 的解析式为： y=−3x+3 ，且 l1 与x轴交于点D，直线 l2 经过点A，B，直线 l1 ， l2 交于点C.

    (1)、求直线 l2 的解析表达式；
    (2)、求 ΔADC 的面积.

    查看试题解析

  • 21. 下图反映的过程是小明从家去菜地浇水，又去玉米地锄草，然后回家．其中x表示时间，y表示小明离他家的距离．根据图象回答下列问题：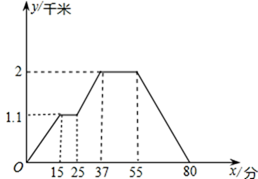

    ①菜地离小明家多远？小明走到菜地用了多少时间？

    ②小明给菜地浇水用了多少时间？

    ③玉米地离菜地、小明家多远？小明从玉米地走回家平均速度是多少？

    查看试题解析

四、综合题

  • 22. 某中学计划暑假期间安排2名老师带领部分学生参加红色旅游.甲､乙两家旅行社的服务质量相同，且报价都是每人1000元，经协商，甲旅行社的优惠条件是：老师､学生都按八折收费：乙旅行社的优惠条件是：两位老师全额收费，学生都按七五折收费，
    (1)、设参加这次红色旅游的老师学生共有 x 名， y甲 ， y乙 （单位：元）分别表示选择甲、乙两家旅行社所需的费用，求 y甲 ， y乙 关于 x 的函数解析式；
    (2)、该校选择哪家旅行社支付的旅游费用较少?

    查看试题解析

  • 23. 甲、乙两家商场平时以同样的价格出售相同的商品.“五一”期间两家商场都让利酬宾，其中甲商场所有商品按 8 折出售，乙商场对一次购物中超过 200 元后的价格部分打 6 折.设 x （单位：元）表示商品原价， y甲 （单位：元）表示在甲商场购物金额， y乙 （单位：元）表示在乙商场购物金额.

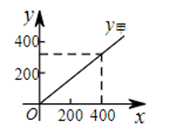    (1)、就两家商场的让利方式分别写出 y甲 ， y乙 关于x的函数解析式；
    (2)、y甲关于x的函数图象如图所示，请在同一直角坐标系中画出 y乙 关于x的函数图象；
    (3)、“五一”期间，如何选择这两家商场去购物更省钱？

    查看试题解析

  • 24. 我市全民健身中心面向学生推出假期游泳优惠活动，活动方案如下：

    方案一：购买一张学生卡，每次游泳费用按六折优惠；

    方案二：不购买学生卡，每次游泳费用按八折优惠．

    设某学生假期游泳x(次)，按照方案一所需费用为y1(元)，且y1=k1x+b；按照方案二所需费用为y2(元)，且y2=k2x．其函数图象如图所示．

    (1)、求y1关于x的函数关系式，并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用；
    (2)、求打折前的每次游泳费用和k2的值；
    (3)、八年级学生小明计划假期前往全民健身中心游泳8次，选择哪种方案所需费用更少？说明理由．

    查看试题解析