北师版数学九年级上册第一次月考试卷A卷
试卷更新日期:2021-09-05 类型:月考试卷
一、单选题
-
1. 一元二次方程 ,配方后可形为( )A、 B、 C、 D、2. 数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是( )
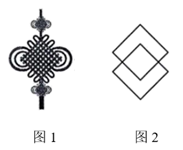 A、用3个相同的菱形放置,最多能得到6个菱形 B、用4个相同的菱形放置,最多能得到16个菱形 C、用5个相同的菱形放置,最多能得到27个菱形 D、用6个相同的菱形放置,最多能得到41个菱形3. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( )
A、用3个相同的菱形放置,最多能得到6个菱形 B、用4个相同的菱形放置,最多能得到16个菱形 C、用5个相同的菱形放置,最多能得到27个菱形 D、用6个相同的菱形放置,最多能得到41个菱形3. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( )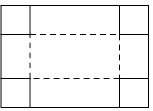 A、(30﹣2x)(40﹣x)=600 B、(30﹣x)(40﹣x)=600 C、(30﹣x)(40﹣2x)=600 D、(30﹣2x)(40﹣2x)=6004. 折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )A、 B、2 C、 D、45. 若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为( )A、 B、4 C、25 D、56. 如图,在矩形ABCD中,AB=5,BC=5 ,点P在线段BC上运动(含B、C两点),连接AP , 以点A为中心,将线段AP逆时针旋转60°到AQ , 连接DQ , 则线段DQ的最小值为( )
A、(30﹣2x)(40﹣x)=600 B、(30﹣x)(40﹣x)=600 C、(30﹣x)(40﹣2x)=600 D、(30﹣2x)(40﹣2x)=6004. 折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )A、 B、2 C、 D、45. 若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为( )A、 B、4 C、25 D、56. 如图,在矩形ABCD中,AB=5,BC=5 ,点P在线段BC上运动(含B、C两点),连接AP , 以点A为中心,将线段AP逆时针旋转60°到AQ , 连接DQ , 则线段DQ的最小值为( )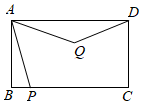 A、 B、 C、 D、37. 已知一元二次方程 的两根为 , ,则 的值为( )A、-7 B、-3 C、2 D、58. 如图,在平行四边形 中, , .连接AC , 过点B作 ,交DC的延长线于点E , 连接AE , 交BC于点F . 若 ,则四边形ABEC的面积为( )
A、 B、 C、 D、37. 已知一元二次方程 的两根为 , ,则 的值为( )A、-7 B、-3 C、2 D、58. 如图,在平行四边形 中, , .连接AC , 过点B作 ,交DC的延长线于点E , 连接AE , 交BC于点F . 若 ,则四边形ABEC的面积为( )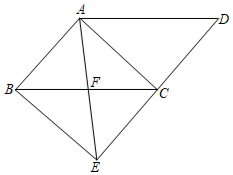 A、 B、 C、6 D、9. 已知方程 的两根分别为 , ,则 的值为( )A、1 B、-1 C、2021 D、-202110. 一个四边形顺次添加下列中的三个条件便得到正方形:
A、 B、 C、6 D、9. 已知方程 的两根分别为 , ,则 的值为( )A、1 B、-1 C、2021 D、-202110. 一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( )
A、仅① B、仅③ C、①② D、②③11. 关于x的方程 有两个实数根 , ,且 ,那么m的值为( )A、-1 B、-4 C、-4或1 D、-1或412. 如图所示,在矩形纸片 中, ,点 分别是矩形的边 上的动点,将该纸片沿直线 折叠.使点 落在矩形边 上,对应点记为点 ,点 落在 处,连接 与 交于点 .则下列结论成立的是( )① ;②当点 与点 重合时 ;③ 的面积 的取值范围是 ;④当 时, .
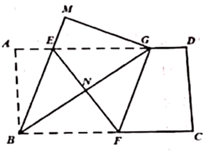 A、①③ B、③④ C、②③ D、②④
A、①③ B、③④ C、②③ D、②④二、填空题
-
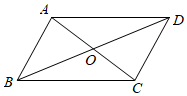
13. 中国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为 .14. 如图,在平行四边形 中,对角线 、 相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使平行四边形 是矩形.
 15. 已知:m2﹣2m﹣1=0,n2+2n﹣1=0且mn≠1,则 的值为 .16. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.
15. 已知:m2﹣2m﹣1=0,n2+2n﹣1=0且mn≠1,则 的值为 .16. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.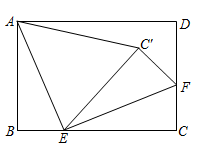 17. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.18. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)
17. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.18. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)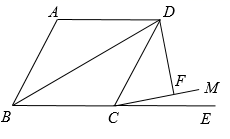
三、解答题
-
19. 解方程:20. 解方程:(x-1)(2x+3)=(2x+3).21. 解下列方程:(1)、x2﹣6x﹣3=0;(2)、3x(x﹣1)=2(1﹣x).22. 如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F , 且AF=AD , 连接BF , 求证:四边形ABFC是矩形.
 23. 已知关于x的一元二次方程x2-(m-3)x-m=0(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两实根为x1、x2 , 且x12+x22-x1x2=7,求m的值。24. 如图,在 中,点O是 的中点,连接 并延长交 的延长线于点E , 连接 、 .
23. 已知关于x的一元二次方程x2-(m-3)x-m=0(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两实根为x1、x2 , 且x12+x22-x1x2=7,求m的值。24. 如图,在 中,点O是 的中点,连接 并延长交 的延长线于点E , 连接 、 . (1)、求证:四边形 是平行四边形;(2)、若 ,判断四边形 的形状,并说明理由.25. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?26. 如图,在 中, 的角平分线交 于点D, .
(1)、求证:四边形 是平行四边形;(2)、若 ,判断四边形 的形状,并说明理由.25. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?26. 如图,在 中, 的角平分线交 于点D, .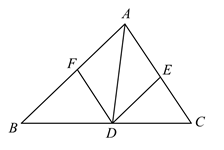 (1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.
(1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.