2021年苏科版数学七年级上册2.3 数轴 同步练习(提优版)
试卷更新日期:2021-09-05 类型:同步测试
一、单选题
-
1. 下列图形是数轴的是A、
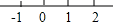 B、
B、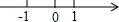 C、
C、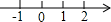 D、
D、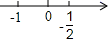 2. A为数轴上表示3的点,将点A沿数轴向左平移7个单位到点B,再由B向右平移6个单位到点C,则点C表示的数是( )A、0 B、1 C、2 D、33. 数轴上两点A、B;其中点A表示的数是2,点B到点A的距离是4个单位长度,则点B表示的数是( )A、6 B、-2 C、±4 D、6或﹣24. 数轴上点A和点B表示的数分别为-4和2,若要使点A到点B的距离是2,则应将点A向右移动( )A、4个单位长度 B、6个单位长度 C、4个单位长度或8个单位长度 D、6个单位长度或8个单位长度5. 如图,将刻度尺放在数轴上(数轴的单位长度是1 cm),刻度尺上“0 cm”和“3 cm”分别对应数轴上的3和0,那么刻度尺上“5.8 cm”对应数轴上的数为( )
2. A为数轴上表示3的点,将点A沿数轴向左平移7个单位到点B,再由B向右平移6个单位到点C,则点C表示的数是( )A、0 B、1 C、2 D、33. 数轴上两点A、B;其中点A表示的数是2,点B到点A的距离是4个单位长度,则点B表示的数是( )A、6 B、-2 C、±4 D、6或﹣24. 数轴上点A和点B表示的数分别为-4和2,若要使点A到点B的距离是2,则应将点A向右移动( )A、4个单位长度 B、6个单位长度 C、4个单位长度或8个单位长度 D、6个单位长度或8个单位长度5. 如图,将刻度尺放在数轴上(数轴的单位长度是1 cm),刻度尺上“0 cm”和“3 cm”分别对应数轴上的3和0,那么刻度尺上“5.8 cm”对应数轴上的数为( ) A、 B、 C、 D、6. 北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下:( )
A、 B、 C、 D、6. 北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下:( )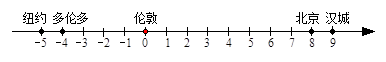
如果将两地国际标准时间的差简称为时差,那么
A、汉城与纽约的时差为13小时 B、汉城与多伦多的时差为13小时 C、北京与纽约的时差为14小时 D、北京与多伦多的时差为14小时7. 小丽在纸上画了一条数轴后,折叠纸面,使数轴上表示1的点与表示-5的点重合;若数轴上A、B两点之间的距离为7(A在B的左侧),且A、B两点经上述折叠后重合,则A点表示的数为( )
A、-3.5 B、3.5 C、-4.5 D、-5.58. 如图是北京地铁一号线部分站点的分布示意图,在图中以正东为正方向建立数轴,有如下四个结论:①当表示天安门东的点所表示的数为0,表示天安门西的点所表示的数为﹣3.5时,表示东单的点所表示的数为6;②当表示天安门东的点所表示的数为0,表示天安门西的点所表示的数为﹣7时,表示东单的点所表示的数为12;③当表示天安门东的点所表示的数为1,表示天安门西的点所表示的数为﹣2.5时,表示东单的点所表示的数为7;④当表示天安门东的点所表示的数为2,表示天安门西的点所表示的数为﹣5时,表示东单的点所表示的数为14;上述结论中,所有正确结论的序号是( )
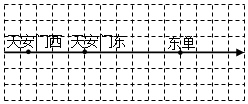 A、①②③ B、②③④ C、①④ D、①②③④9. 如图所示,将圆的周长分为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数1所对应的点重合,再让圆沿着数轴按逆时针方向滚动,那么数轴上的数 -2020将与圆周上的数字( )重合.
A、①②③ B、②③④ C、①④ D、①②③④9. 如图所示,将圆的周长分为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数1所对应的点重合,再让圆沿着数轴按逆时针方向滚动,那么数轴上的数 -2020将与圆周上的数字( )重合. A、0 B、1 C、2 D、310. 点A,B是数轴上两点,位置如图,点P,Q是数轴上两动点,点P由点A点出发,以1单位长度/秒的速度在数轴上运动,点Q由点B点出发,以2单位长度/秒的速度在数轴上运动.若两点同时开始和结束运动,设运动时间为t秒.下面是四位同学的判断:
A、0 B、1 C、2 D、310. 点A,B是数轴上两点,位置如图,点P,Q是数轴上两动点,点P由点A点出发,以1单位长度/秒的速度在数轴上运动,点Q由点B点出发,以2单位长度/秒的速度在数轴上运动.若两点同时开始和结束运动,设运动时间为t秒.下面是四位同学的判断:①小康同学:当t=2时,点P和点Q重合.
②小柔同学:当t=6时,点P和点Q重合.
③小议同学:当t=2时,PQ=8.
④小科同学:当t=6时,PQ=18.
以上说法可能正确的是( )
 A、①②③ B、②③④ C、①③④ D、①②③④
A、①②③ B、②③④ C、①③④ D、①②③④二、填空题
-
11. 在数轴上表示 与 的两个点之间的距离是.12. M、N是数轴上的两个点,线段MN的长度为3,若点M表示的数为-1,则点N表示的数为.13. 已知A、B是数轴上的点,点A向左移动3个单位长度后与点B重合.若点B表示的数是 ,则点A表示的数是.14. 若数轴上点A到原点的距离为3,点B到原点的距离为5,则A、B两点的距离为 .15. 点A,点B在数轴上分别表示 6.5,x.点B在点A的左边,且点A,点B之间有9个整数,则x的取值范围为 .16. 数轴上表示的数是整数的点称为整点,某数轴的单位长度是1cm,若在这个数轴上任意画出一条长2000cm的线段AB,则线段AB盖住的整点的个数是.17. 如图,已知数轴上的点C表示的数为6,点A表示的数为-4,点B是AC的中点,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,运动时间为1秒(t> 0),另一动点Q,从B出发,以每秒1个单位长度的速度沿数轴向左匀速运动,且P,Q同时出发,当t为秒时,点P与点Q之间的距离为2个单位长度。
 18. 如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第1次点A向左移动3个单位长度至点A1 , 第2次从点A1向右移动6个单位长度至点A2 , 第3次从点A2向左移动9个单位长度至点A3 , …,按照这种移动方式进行下去,点A4表示的数,是 , 如果点An与原点的距离不小于20,那么n的最小值是 .
18. 如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第1次点A向左移动3个单位长度至点A1 , 第2次从点A1向右移动6个单位长度至点A2 , 第3次从点A2向左移动9个单位长度至点A3 , …,按照这种移动方式进行下去,点A4表示的数,是 , 如果点An与原点的距离不小于20,那么n的最小值是 .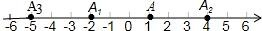
三、解答题
-
19. 一只电子蚂蚁在数轴上从-3出发向左运动2个单位长度到点A处,再向右运动4个单位长度到点C处.
(1)画出数轴标出A、C所表示的数;
(2)这只电子蚂蚁一共运动多少个单位长度?20. 已知A,B两点在数轴上表示的数分别是 和12,现A,B两点分别以1个单位/秒,3个单位秒的速度向左运动,A比B早1秒出发,问B出发后几秒原点恰好在两点正中间? 21. 已知快递公司坐落在一条东西走向的街道上,某快递员从快递公司取件后在这条街道上送快递,他先向东骑行1千米到达A店,继续向东骑行2千米到达B店,然后向西骑行5千米到达C店,最后回到快递公司。(1)、以快递公司为原点,以向东方向为正方向,用1厘米表示1千米,画出数轴,并在数轴上表示出A,B,C三个店的位置。(2)、C店离A店有多远?(3)、快递员一共骑行了多少千米?22. 如图A在数轴上所对应的数为﹣2.
21. 已知快递公司坐落在一条东西走向的街道上,某快递员从快递公司取件后在这条街道上送快递,他先向东骑行1千米到达A店,继续向东骑行2千米到达B店,然后向西骑行5千米到达C店,最后回到快递公司。(1)、以快递公司为原点,以向东方向为正方向,用1厘米表示1千米,画出数轴,并在数轴上表示出A,B,C三个店的位置。(2)、C店离A店有多远?(3)、快递员一共骑行了多少千米?22. 如图A在数轴上所对应的数为﹣2.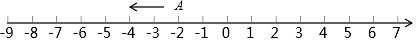 (1)、点B在点A右边距A点4个单位长度,求点B所对应的数;(2)、在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.(3)、在(2)的条件下,现A点静止不动,B点沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.23.
(1)、点B在点A右边距A点4个单位长度,求点B所对应的数;(2)、在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.(3)、在(2)的条件下,现A点静止不动,B点沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.23.如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.

(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C表示的数是什么数 ,这个数是多少;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是多少;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3
①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
24. 如图,在一条不完整的数轴上从左到右有点A , B , C , 其中AB=2BC , 设点A , B , C所对应数的和是m . (1)、若点C为原点,BC=1,则点A , B所对应的数分别为 , , m的值为;(2)、若点B为原点,AC=6,求m的值.(3)、若原点O到点C的距离为8,且OC=AB , 求m的值.25. 已知在纸面上有一数轴(如图),折叠纸面.(1)、若1表示的点与-1表示的点重合,则-7表示的点与数表示的点重合;(2)、若-1表示的点与5表示的点重合,回答以下问题:
(1)、若点C为原点,BC=1,则点A , B所对应的数分别为 , , m的值为;(2)、若点B为原点,AC=6,求m的值.(3)、若原点O到点C的距离为8,且OC=AB , 求m的值.25. 已知在纸面上有一数轴(如图),折叠纸面.(1)、若1表示的点与-1表示的点重合,则-7表示的点与数表示的点重合;(2)、若-1表示的点与5表示的点重合,回答以下问题:①13表示的点与数表示的点重合;
②若数轴上A、B两点之间的距离为2015(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
26. 如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是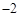 。
。 
已知点A是数轴上的点,完成下列各题:
(1)、如果点A表示的数是3,将点A先向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是 , A、B两点间的距离为;(2)、如果点A表示的数是-4,将点A先向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是 , A、B两点间的距离为;(3)、一般地,如果点A表示的数是m,将点A先向右移动n个单位长度,再向左移动t个单位长度,那么终点B表示的数是 , A、B两点间的距离为。