初中数学人教版九年级上册——第二十二章二次函数检测题③
试卷更新日期:2021-09-05 类型:单元试卷
一、单选题
-
1. 下列函数中,是二次函数的是( )A、y=ax2+bx+c B、y=(x+2)(x﹣2)﹣x2 C、y= D、y=(x-3)x2. 二次函数 的图像大致为( )A、
 B、
B、 C、
C、 D、
D、 3. 函数y=ax2+ax+a(a≠0)的图象可能是下列图象中的( )A、
3. 函数y=ax2+ax+a(a≠0)的图象可能是下列图象中的( )A、 B、
B、 C、
C、 D、
D、 4. 抛物线y= ,y=x2 , y=﹣x2的共同性质是:
4. 抛物线y= ,y=x2 , y=﹣x2的共同性质是:①都是开口向上;
②都以点(0,0)为顶点;
③都以y轴为对称轴;
④都关于x轴对称.
其中正确的个数有( )
A、1个 B、2个 C、3个 D、4个5. 在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是( )A、y=(x+1)2+1 B、y=(x﹣3)2+1 C、y=(x﹣3)2﹣5 D、y=(x+1)2+26. 长方形的周长为24cm,其中一边为x(其中x>0),面积为ycm2 , 则这样的长方形中y与x的关系可以写为( )
A、y=x2 B、y=(12﹣x2) C、y=(12﹣x)•x D、y=2(12﹣x)7. 如图,抛物线y=ax2+bx+c与x轴的负半轴交于点A,B(点A在点B的右边),与y轴的正半轴交于点C,且OA=OC=1,则下列关系中正确的是( )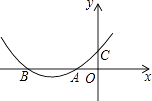 A、a+b=1 B、b<2a C、a﹣b=﹣1 D、ac<08. 关于二次函数 ,下列说法错误的是( )A、若将图象向上平移10个单位,再向左平移2个单位后过点 ,则 B、当 时,y有最小值 C、 对应的函数值比最小值大7 D、当 时,图象与x轴有两个不同的交点9. 已知二次函数y=x2-4x+2,若-1≤x≤1时,则y的取值范围( )A、y≥ 7 B、y≤-1 C、-1≤y≤7 D、-2≤y≤710. 二次函数 的图象如图所示,下列结论中:① ;② ( 的实数);③ ;④在 中存在一个实数 、使得 其中正确的有( )
A、a+b=1 B、b<2a C、a﹣b=﹣1 D、ac<08. 关于二次函数 ,下列说法错误的是( )A、若将图象向上平移10个单位,再向左平移2个单位后过点 ,则 B、当 时,y有最小值 C、 对应的函数值比最小值大7 D、当 时,图象与x轴有两个不同的交点9. 已知二次函数y=x2-4x+2,若-1≤x≤1时,则y的取值范围( )A、y≥ 7 B、y≤-1 C、-1≤y≤7 D、-2≤y≤710. 二次函数 的图象如图所示,下列结论中:① ;② ( 的实数);③ ;④在 中存在一个实数 、使得 其中正确的有( ) A、 个 B、 个 C、 个 D、 个
A、 个 B、 个 C、 个 D、 个二、填空题
-
11. 二次函数 的图象开口向上且过原点,则a=.12. 如图,抛物线 与直线 的两个交点坐标分别为 , ,则关于x的方程 的解为.
 13. 已知抛物线y=x2﹣4x+m与x轴交于A、B两点,若A的坐标是(﹣1,0),则B的坐标是 .14. 如图,小滕用铁栅栏及一面墙(墙足够长)围成了一个矩形自行车场地ABCD,在AB和BC边各有一个2m宽的小门(不用铁栅栏),小滕共用了铁栅栏40米,则矩形ABCD的面积的最大值为m2.
13. 已知抛物线y=x2﹣4x+m与x轴交于A、B两点,若A的坐标是(﹣1,0),则B的坐标是 .14. 如图,小滕用铁栅栏及一面墙(墙足够长)围成了一个矩形自行车场地ABCD,在AB和BC边各有一个2m宽的小门(不用铁栅栏),小滕共用了铁栅栏40米,则矩形ABCD的面积的最大值为m2.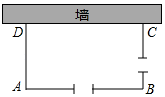 15. 已知 , 是抛物线 上的两点,且 ,若 ,则 (填“ ”、“ ”或“ ”)16. 若抛物线C1:y=x2+mx+2与抛物线C2:y=x2﹣3x+n关于y轴对称,则m+n=.
15. 已知 , 是抛物线 上的两点,且 ,若 ,则 (填“ ”、“ ”或“ ”)16. 若抛物线C1:y=x2+mx+2与抛物线C2:y=x2﹣3x+n关于y轴对称,则m+n=.三、解答题
-
17. 已知二次函数y=x2﹣2mx+m2+3(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?
(3)将抛物线y=x2﹣2mx+m2+3(m是常数)图象在对称轴左侧部分沿直线y=3翻折得到新图象为G,若与直线y=x+2有三个交点,请直接写出m的取值范围.
18. 汽车租赁行业现在火爆起来.小明开办了一家汽车租赁公司,拥有汽车20辆,在旺季每辆车的每天租金为600元时,可全部租出:当每辆车的每天租金增加50元时,未租出的车将增加一辆,租出的车辆每辆每天需要维护费200元,未租出的车辆每辆每天需要维护费100元,每天其他开销共计1000元.(1)当每辆车的租金为1000元时,每天能租出多少辆车?每天净收益为多少元?
(2)当每辆车的每天租金定为多少元时,租赁公司的每天净收益最大?最大净收益为多少元?(每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销)
19. 如图,点 在函数 的图象上.已知 的横坐标分别为-2、4,直线 与 轴交于点 ,连接 .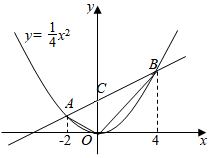 (1)、求直线 的函数表达式;(2)、求 的面积;(3)、若函数 的图象上存在点 ,使得 的面积等于 的面积的一半,则这样的点 共有个.
(1)、求直线 的函数表达式;(2)、求 的面积;(3)、若函数 的图象上存在点 ,使得 的面积等于 的面积的一半,则这样的点 共有个.