初中数学人教版九年级上册——22.2二次函数与一元二次方程
试卷更新日期:2021-09-05 类型:同步测试
一、单选题
-
1. 二次函数 (a,b,c为常数,且 )中的x与y的部分对应值如下表:
x
-1
0
1
3
y
-1
3
5
3
下列结论:① ;② ;③当 时,y随着x的增大而减小;④-1和3是方程 的根,其中正确的个数为( )
A、1个 B、2个 C、3个 D、4个2. 如图,是抛物线 ( )图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线 ( )与抛物线交于A,B两点,下列结论:① ; ②抛物线与x轴的另一个交点是( ,0);③方程 有两个相等的实数根;④当时 ,有 ;⑤若 ,且 ;则 .则命题正确的个数为( )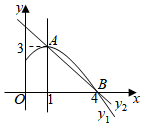 A、5个 B、4个 C、3个 D、2个3. 如图,抛物线 的对称轴为直线 ,若关于 的一元二次方程 ( 为实数)在 的范围内有解,则 的取值错误的是( )
A、5个 B、4个 C、3个 D、2个3. 如图,抛物线 的对称轴为直线 ,若关于 的一元二次方程 ( 为实数)在 的范围内有解,则 的取值错误的是( )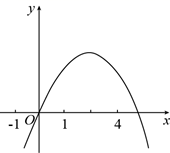 A、 B、 C、 D、4. 若函数 的图象如图所示,则关于x的一元二次方程 的根的情况为( )
A、 B、 C、 D、4. 若函数 的图象如图所示,则关于x的一元二次方程 的根的情况为( ) A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 已知二次函数y=﹣ +bx+c的图象经过(﹣1,0)与(5,0)两点,且关于x的方程﹣x2+bx+c+d=0有两个根,其中一个根是6,则d的值为( )A、5 B、7 C、12 D、﹣76. 关于x的一元二次方程 (t为实数)有且只有一个根在 的范围内,则t的取值范围是( )A、 B、 C、 或 D、7. 已知二次函数y=ax2+bx+c,且a<0,a-b+c>0,则一定有( )A、 B、 C、 D、8. 若方程ax2+bx+c=0(a>0)的两个根是﹣3和1,则对于二次函数y=ax2+bx+c,当y>0时,x的取值范围是( )A、﹣3<x<1 B、x<﹣3或x>1 C、x>﹣3 D、x<19. 根据下列表格的对应值:判断方程ax2+bx+c=0(a≠0)的一个根x的大致范围是( )
A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 已知二次函数y=﹣ +bx+c的图象经过(﹣1,0)与(5,0)两点,且关于x的方程﹣x2+bx+c+d=0有两个根,其中一个根是6,则d的值为( )A、5 B、7 C、12 D、﹣76. 关于x的一元二次方程 (t为实数)有且只有一个根在 的范围内,则t的取值范围是( )A、 B、 C、 或 D、7. 已知二次函数y=ax2+bx+c,且a<0,a-b+c>0,则一定有( )A、 B、 C、 D、8. 若方程ax2+bx+c=0(a>0)的两个根是﹣3和1,则对于二次函数y=ax2+bx+c,当y>0时,x的取值范围是( )A、﹣3<x<1 B、x<﹣3或x>1 C、x>﹣3 D、x<19. 根据下列表格的对应值:判断方程ax2+bx+c=0(a≠0)的一个根x的大致范围是( )x
6.17
6.18
6.19
6.20
ax2+bx+c
−0.03
−0.01
0.02
0.04
A、6.19<x<6.20 B、6.18<x<6.19 C、6.17<x<6.18 D、6<x<6.1710. 如图,一次函数y1=2x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣2)x+c的图象可能是( )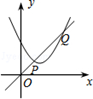 A、
A、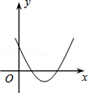 B、
B、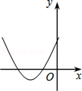 C、
C、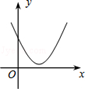 D、
D、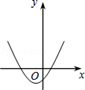
二、填空题
-
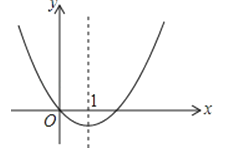
11. 已知抛物线 与 轴交点的坐标分别为 , ,则一元二次方程 的根为.12. 若一元二次方程2x2﹣2x+m=0有实数根,则m的取值范围是.13. 抛物线y=ax2+bx+c经过A(﹣1,4),B(2,4),则关于x的一元二次方程a(x﹣3)2﹣4=3b﹣bx﹣c的解为.14. 将二次函数 的图象向左平移1个单位,再向上平移1个单位若得到的函数图象与直线 有两个交点,则a的取值范围是.15. 二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是 .
 16. 如图,已知顶点为 的抛物线 经过点 ,下列结论:① ;② ;③若点 在抛物线上,则 ;④关于 的一元二次方程 的两根为 和 ,其中正确的是.
16. 如图,已知顶点为 的抛物线 经过点 ,下列结论:① ;② ;③若点 在抛物线上,则 ;④关于 的一元二次方程 的两根为 和 ,其中正确的是.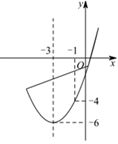
三、解答题
-
17. 已知二次函数 .求证:不论 为何实数,此二次函数的图象与 轴都有两个不同交点.18. 已知二次函数 .(1)、求证:二次函数的图象必过点 ;(2)、若点 , 在函数图象上, ,求该函数的表达式;(3)、若该函数图象与x轴有两个交点 , ,求证: .19. 如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.
 (1)、求抛物线的解析式;(2)、过点A的直线交直线BC于点M.
(1)、求抛物线的解析式;(2)、过点A的直线交直线BC于点M.①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.