初中数学浙教版八年级上册第3章 一元一次不等式单元检测
试卷更新日期:2021-09-05 类型:单元试卷
一、单选题
-
1. 我市某一天的最高气温是30℃,最低气温是20℃,则当天我市气温t(℃)( )A、20<t<30 B、20≤t≤30 C、20≤t<30 D、20<t≤302. 若 ,则下列各式中错误的是( )A、 B、 C、 D、3. 不等式 的解集在数轴上表示正确的是( )A、
 B、
B、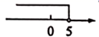 C、
C、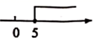 D、
D、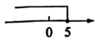 4. 已知a、b、c均为实数,若a>b,c≠0,下列结论不一定正确的是( )A、a+c>b+c B、c-a<c-b C、 D、a2>ab>b25. 已知m<n , 则下列不等式中错误的是( )A、3m<3n B、m+1<n+1 C、m﹣n<0 D、﹣m<﹣n6. 若 是关于x的不等式 的一个解,则a的取值范围是( )A、 B、 C、 D、7. 下列说法正确的是( )A、x=2不是不等式x+2>2的解 B、x=2是不等式x+2>2的解集 C、方程x+y=3无解 D、不等式x+2>2有无数个解8. 不等式 的解集是( )A、 B、 C、 D、9. 解集是如图所示的不等式组为( )
4. 已知a、b、c均为实数,若a>b,c≠0,下列结论不一定正确的是( )A、a+c>b+c B、c-a<c-b C、 D、a2>ab>b25. 已知m<n , 则下列不等式中错误的是( )A、3m<3n B、m+1<n+1 C、m﹣n<0 D、﹣m<﹣n6. 若 是关于x的不等式 的一个解,则a的取值范围是( )A、 B、 C、 D、7. 下列说法正确的是( )A、x=2不是不等式x+2>2的解 B、x=2是不等式x+2>2的解集 C、方程x+y=3无解 D、不等式x+2>2有无数个解8. 不等式 的解集是( )A、 B、 C、 D、9. 解集是如图所示的不等式组为( ) A、 B、 C、 D、10. 若关于x的不等式组 的所有整数解的和为0,则m的值不可能是( )A、3 B、3.5 C、3.7 D、4
A、 B、 C、 D、10. 若关于x的不等式组 的所有整数解的和为0,则m的值不可能是( )A、3 B、3.5 C、3.7 D、4二、填空题
-
11. 已知a的2倍比1大,其数量关系用不等式表示.12. “ 的2倍与 的差小于 ”用不等式表示.13. 已知m、n是整数,如果关于x的不等式组 仅有三个整数解:﹣1,0,1,则mn的值为 .14. 甲、乙两队进行篮球对抗赛,每场比赛都要分出胜负,比赛规定每队胜1场得3分,负1场扣1分,两队一共比赛了10场,若甲队得分不低于14分,则甲队至少要胜场.15. 自主创业的小李经营一家工厂、生产甲、乙两种产品.根据生产规定,每件甲产品需分别在一台 设备上加工 小时,一台 设备上加工 小时,每件可获得利润 元;每件乙产品需分别在一台 设备上加工4小时,一台 设备上加工 小时,每件可获得利润 元.已知 设备、 设备、 设备各只有一台,且每天最多能加工的时间分别是 小时,要使每天的利润不低于 元,每天可生产甲产品件,乙产品件.(写出一种满足条件的生产方案即可)16. 某学校的编程课上,一位同学设计了一个运算程序,如图所示.按上述程序进行运算,程序运行到“判断结果是否大于23”为一次运行.若该程序只运行了2次就停止了,则x的取值范围是.

三、解答题
-
17. 把下列不等式化成x>a或x<a的形式.
(1)2x+5>3;
(2)﹣6(x﹣1)<0.
18. 赵军说不等式2a>3a永远不会成立,因为如果在这个不等式两边同除以a,就会出现2>3这样的错误结论.你同意他的说法对吗?若同意说明其依据,若不同意说出错误的原因.19. 某种饮料重约300g,罐上注有“蛋白质含量≥0.5%”,其中蛋白质的含量为多少克?20. 已知关于x的不等式(1﹣a)x>2,两边都除以(1﹣a),得x< , 试化简:|a﹣1|+|a+2|.21. 解不等式(组),并在数轴上表示解集:(1)、(2)、22. 根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:若a﹣b>0,则a>b;若a﹣b=0,则a=b;若a﹣b<0,则a<b.反之也成立.这种比较大小的方法称为“求差法比较大小”.请运用这种方法尝试解决下面的问题:
(1)、比较4+3a2﹣2b+b2与3a2﹣2b+1的大小;(2)、若2a+2b﹣1>3a+b,则a、b的大小关系(直接写出答案).23. 新冠疫情期间,某校九年级提前开学,根据政府疫情防控要求,学校后勤部老师购买了一批 口罩.由于疫情得到很好的拉制,七八年级的同学相继返校,学校后勤部老师又购买了一批一次性医用口罩,但物资清单不慎被墨汁覆盖,老师只记得 口罩的单价比一次性医用口罩的单价多12元,两次购买的数量相同.疫情物资清单
口罩类型
单价(元/个)
总费用(元)
数量(个)
15000
一次性
3000
(1)、两种类型口罩的单价备是多少元?(2)、后来一位爱心人士捐资6000元到学校用于购买口罩,学校还需要600个口罩,后勤部老师最多可以购买多少个 口罩?24. 某学校组织师生共300人参加一次社会实践活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个。(1)、求每辆大客车和每辆小客车的乘客座位数;(2)、由于最后参加活动的人数增加了30人,学校决定调整租车方案.在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值。25. 为了更好地保护环境,污水处理公司决定购买10台甲、乙两种型号的污水处理设备,经调查,购买一台甲型设备比购买一台乙型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元.(1)、求甲、乙两种型号设备每台各多少万元?(2)、已知甲型设备每月处理污水240吨,乙型设备每月处理污水200吨,该地每月需要处理的污水不低于2040吨.若污水处理公司购买污水处理设备的资金不超过105万元,请你为污水处理公司设计一种最省钱的购买方案。