湘教版数学九年级上册《 第3章 图形的相似》单元测试B卷
试卷更新日期:2021-09-04 类型:单元试卷
一、单选题
-
1. 若 ,且 ,则 的值是( )A、2 B、4 C、6 D、82. 下列四组线段中,是成比例线段的是( )A、2cm,3cm,4cm,5cm B、3cm,6cm,0.2dm,5cm C、2cm,4cm,6cm,8cm D、12cm,8cm,15cm,10cm3. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( )
 A、 B、 C、1 D、4. 如图,矩形OABC的面积为36,它的对角线OB与双曲线y 相交于点D , 且OD:OB=2:3,则k的值为( )
A、 B、 C、1 D、4. 如图,矩形OABC的面积为36,它的对角线OB与双曲线y 相交于点D , 且OD:OB=2:3,则k的值为( )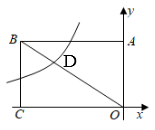 A、12 B、﹣12 C、16 D、﹣165. 如图,四边形ABCD是平行四边形,点E在CD边上,则下列结论错误的是( )
A、12 B、﹣12 C、16 D、﹣165. 如图,四边形ABCD是平行四边形,点E在CD边上,则下列结论错误的是( ) A、 B、 C、 D、6. 如图, 、 交于 点, ,则下列结论一定正确的是( )
A、 B、 C、 D、6. 如图, 、 交于 点, ,则下列结论一定正确的是( ) A、 B、 C、 D、7. 如图,在平面直角坐标系中,矩形 与矩形 是以点 为位似中心的位似图形,点 的坐标为 ,若 ,则 的长是( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,矩形 与矩形 是以点 为位似中心的位似图形,点 的坐标为 ,若 ,则 的长是( ) A、3 B、4 C、4.5 D、68. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( )
A、3 B、4 C、4.5 D、68. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( ) A、2 B、4 C、6 D、89. 下列四个命题:①直径是圆的对称轴;②若两个相似四边形的相似比是1:3,则它们的周长比是1:3,面积比是1:6;③同一平面内垂直于同一直线的两条直线互相平行;④对角线相等且互相垂直的平行四边形是正方形.其中真命题有( )A、①③ B、①④ C、③④ D、②③④10. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )
A、2 B、4 C、6 D、89. 下列四个命题:①直径是圆的对称轴;②若两个相似四边形的相似比是1:3,则它们的周长比是1:3,面积比是1:6;③同一平面内垂直于同一直线的两条直线互相平行;④对角线相等且互相垂直的平行四边形是正方形.其中真命题有( )A、①③ B、①④ C、③④ D、②③④10. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )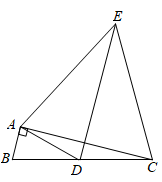 A、 B、 C、 D、211. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的相似比是( )
A、 B、 C、 D、211. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的相似比是( )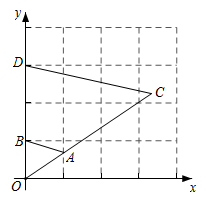 A、2:1 B、1:2 C、3:1 D、1:312. 如图,平行四边形 的对角线 、 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( )
A、2:1 B、1:2 C、3:1 D、1:312. 如图,平行四边形 的对角线 、 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( ) A、5.5 B、5 C、4 D、3
A、5.5 B、5 C、4 D、3二、填空题
-
13. 若 ,则 .14. 若 , , , 是成比例线段,其中 , , ,则线段 .15. 如图,△ABC中,AB=AC,∠B=72°,∠ACB的平分线CD交AB于点D,则点D是线段AB的黄金分割点.若AC=2,则BD=.
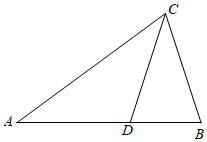 16. 如图,矩形ABCD中,AD AB , 点E在BC边上,且AE=AD , DF⊥AE于点F , 连接DE , BF , BF的延长线交DE于点O , 交CD于点G . 以下结论:①AF=DC , ②OF:BF=CE:CG , ③S△BCG S△DFG , ④图形中相似三角形有6对,则正确结论的序号是 .
16. 如图,矩形ABCD中,AD AB , 点E在BC边上,且AE=AD , DF⊥AE于点F , 连接DE , BF , BF的延长线交DE于点O , 交CD于点G . 以下结论:①AF=DC , ②OF:BF=CE:CG , ③S△BCG S△DFG , ④图形中相似三角形有6对,则正确结论的序号是 . 17. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=.
17. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=. 18. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.
18. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.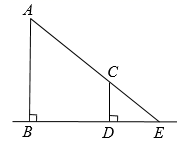
三、解答题
-
19. △ABC在边长为l的正方形网格中如图所示.
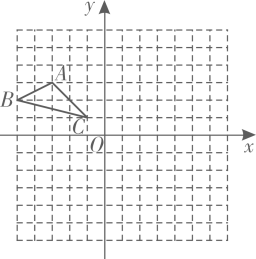
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
20. 如图,利用标杆 测量楼高,点A,D,B在同一直线上, , ,垂足分别为E,C.若测得 , , ,楼高 是多少? 21. 如图,边长为1的正方形 中,点E为 的中点.连接 ,将 沿 折叠得到 交 于点G , 求 的长.
21. 如图,边长为1的正方形 中,点E为 的中点.连接 ,将 沿 折叠得到 交 于点G , 求 的长.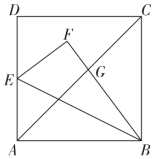 22. 如图,在平行四边形 中,E为 边的中点,连接 ,若 的延长线和 的延长线相交于点F.
22. 如图,在平行四边形 中,E为 边的中点,连接 ,若 的延长线和 的延长线相交于点F.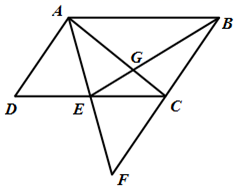 (1)、求证: ;(2)、连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.23. 如图,在 中,点E、F分别在边 、 上,且 .
(1)、求证: ;(2)、连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.23. 如图,在 中,点E、F分别在边 、 上,且 .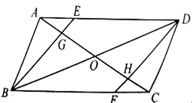 (1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.24. 如图,在正方形ABCD中,点E,F分别为边BC,CD上的点,且AE⊥BF于点P,G为AD的中点,连接GP,过点P作PH⊥GP交AB于点H,连接GH.
(1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.24. 如图,在正方形ABCD中,点E,F分别为边BC,CD上的点,且AE⊥BF于点P,G为AD的中点,连接GP,过点P作PH⊥GP交AB于点H,连接GH. (1)、求证:BE=CF;(2)、若AB=6,BE BC,求GH的长.25. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .
(1)、求证:BE=CF;(2)、若AB=6,BE BC,求GH的长.25. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .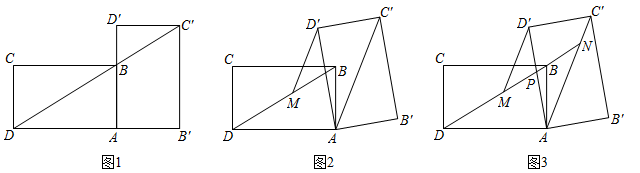
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.