湘教版数学九年级上册同步训练《3.5 相似三角形的应用》
试卷更新日期:2021-09-03 类型:同步测试
一、单选题
-
1. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )
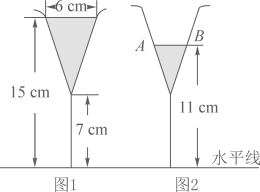 A、 B、 C、 D、2. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、3. 大约在两千四五百年前,如图1墨子和他的学生做了世界上第一个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为 ,像距为 ,蜡烛火焰倒立的像的高度是 ,则蜡烛火焰的高度是( )
A、 B、 C、 D、2. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、3. 大约在两千四五百年前,如图1墨子和他的学生做了世界上第一个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为 ,像距为 ,蜡烛火焰倒立的像的高度是 ,则蜡烛火焰的高度是( )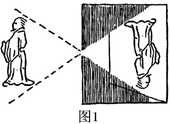
 A、 B、 C、 D、4. 某校兴趣小组为了测量教学大楼的高度,用1.5m的竹竿作为测量工具.在阳光明媚的某天,该兴趣小组移动竹竿,使得竹竿顶端的影子与楼顶的影子在地面 处重合,如图,测得 , ,则教学楼 的高是( )
A、 B、 C、 D、4. 某校兴趣小组为了测量教学大楼的高度,用1.5m的竹竿作为测量工具.在阳光明媚的某天,该兴趣小组移动竹竿,使得竹竿顶端的影子与楼顶的影子在地面 处重合,如图,测得 , ,则教学楼 的高是( ) A、 B、 C、 D、5. 如图,阳光透过窗户洒落在地面上,已知窗户 高 ,光亮区的顶端距离墙角 ,光亮区的底端距离墙角 ,则窗户的底端距离地面的高度( )为( )
A、 B、 C、 D、5. 如图,阳光透过窗户洒落在地面上,已知窗户 高 ,光亮区的顶端距离墙角 ,光亮区的底端距离墙角 ,则窗户的底端距离地面的高度( )为( ) A、 B、 C、 D、6. 如图,为了测量某棵树的高度,小刚用长为2m的竹竿作测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距6m,与树距15m,那么这颗树的高度为( )
A、 B、 C、 D、6. 如图,为了测量某棵树的高度,小刚用长为2m的竹竿作测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距6m,与树距15m,那么这颗树的高度为( )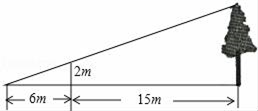 A、5m B、7m C、7.5m D、21m7. 如图,在三角形纸片中, , , .将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )
A、5m B、7m C、7.5m D、21m7. 如图,在三角形纸片中, , , .将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )



 A、①②③ B、①②④ C、①③④ D、①②③④8. 如图,身高1.5米的小西站在点D处,此时路灯M照射的影子AD为2.5米,小西沿着 的方向行走4.5米至点F,此时影子 为1米,则路灯BM的高度为( )
A、①②③ B、①②④ C、①③④ D、①②③④8. 如图,身高1.5米的小西站在点D处,此时路灯M照射的影子AD为2.5米,小西沿着 的方向行走4.5米至点F,此时影子 为1米,则路灯BM的高度为( )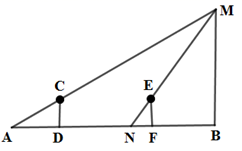 A、3米 B、3.5米 C、4.5米 D、6米9. 如图,锐角三角形 ,边 ,高 ,其内接的正方形的一边在 上,其余两个顶点分别在 , 上,则正方形的边长 为( )
A、3米 B、3.5米 C、4.5米 D、6米9. 如图,锐角三角形 ,边 ,高 ,其内接的正方形的一边在 上,其余两个顶点分别在 , 上,则正方形的边长 为( )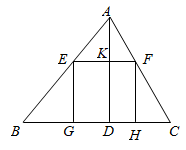 A、2.6 B、2.4 C、3 D、1.210. 如图,在数学实践活动课上,小明同学打算通过测量树的影长计算树的高度,阳光下他测得长1m的竹竿落在地面上的影长为0.9m,在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上,他测得这棵树落在地面上的影长BD为2.7m,落在墙面上的影长CD为1.0m,则这棵树的高度是( )
A、2.6 B、2.4 C、3 D、1.210. 如图,在数学实践活动课上,小明同学打算通过测量树的影长计算树的高度,阳光下他测得长1m的竹竿落在地面上的影长为0.9m,在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上,他测得这棵树落在地面上的影长BD为2.7m,落在墙面上的影长CD为1.0m,则这棵树的高度是( )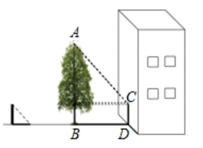 A、6.0m B、5.0m C、4.0m D、3.0m
A、6.0m B、5.0m C、4.0m D、3.0m二、填空题
-
11. 如图,已知李明的身高为1.8m,他在路灯下的影长为2m,李明距路灯杆底部为3m,则路灯灯泡距地面的高度为m;
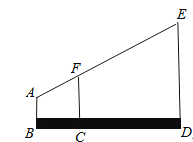
 12. 《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形 ,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线 与边 相交于点F,如果测得 米,那么塔与树的距离 为米.
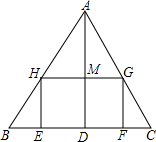
12. 《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形 ,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线 与边 相交于点F,如果测得 米,那么塔与树的距离 为米. 13. 如图,已知在 中, , , ,正方形 的顶点G、F分别在边 、 上,点D、E在斜边 上,那么正方形 的边长为 .
13. 如图,已知在 中, , , ,正方形 的顶点G、F分别在边 、 上,点D、E在斜边 上,那么正方形 的边长为 . 14. 如图所示是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的半径为0.8m,桌面距离地面1m,若灯泡距离地面3m,则地面上阴影部分的面积为m2(结果保留 .
14. 如图所示是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的半径为0.8m,桌面距离地面1m,若灯泡距离地面3m,则地面上阴影部分的面积为m2(结果保留 . 15. 如图, 是 内一点,过点 分别作直线平行于 各边,形成三个小三角形面积分别为 ,则
15. 如图, 是 内一点,过点 分别作直线平行于 各边,形成三个小三角形面积分别为 ,则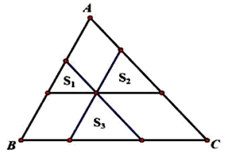 16. 如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为m.
16. 如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为m.
三、解答题
-
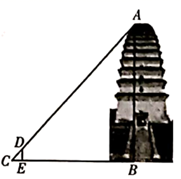
17. 小雁塔位于西安市南郊的荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.数学活动小组的同学对该塔进行了测量,测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为38米,塔的顶端为点A,且 ,在点E处竖直放一根标杆,其顶端为D, ,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得 米.已知标杆 米,求该塔的高度AB.
 18. 身高1.6米的张军同学在某一时刻测得自己的影长为1.4米,此刻她想测量学校旗杆的高度,但当她马上测量旗杆的影长时,发现因旗杆靠近一幢建筑物,影子一部分落在地面上,一部分落在墙上(如图),他先测得留在墙上的影子 米,又测地面部分的影长 米,你能根据上述数据帮张军同学测出旗杆的高度吗?
18. 身高1.6米的张军同学在某一时刻测得自己的影长为1.4米,此刻她想测量学校旗杆的高度,但当她马上测量旗杆的影长时,发现因旗杆靠近一幢建筑物,影子一部分落在地面上,一部分落在墙上(如图),他先测得留在墙上的影子 米,又测地面部分的影长 米,你能根据上述数据帮张军同学测出旗杆的高度吗? 19. 如图,为了估算河的宽度,我们可以在河对岸选定一点A,再在河的这一边选定点B和点C,使得AB⊥BC,然后选定点E,使EC⊥BC,确定BC与AE的交点D,若测得BD=180米,DC=60米,EC=50米,你能知道小河的宽是多少吗?
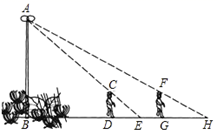
19. 如图,为了估算河的宽度,我们可以在河对岸选定一点A,再在河的这一边选定点B和点C,使得AB⊥BC,然后选定点E,使EC⊥BC,确定BC与AE的交点D,若测得BD=180米,DC=60米,EC=50米,你能知道小河的宽是多少吗?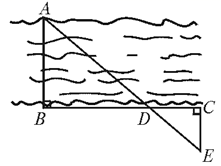 20. 如图,花丛中一根灯杆 上有一盏路灯 ,灯光下,小明在 点处的影长 米,沿 方向走到点 , 米,这时小明的影长 米,如果小明的身高为1.7米,求路灯 离地面的高度.
20. 如图,花丛中一根灯杆 上有一盏路灯 ,灯光下,小明在 点处的影长 米,沿 方向走到点 , 米,这时小明的影长 米,如果小明的身高为1.7米,求路灯 离地面的高度.