湘教版数学九年级上册同步训练《3.4 相似三角形的判定与性质》
试卷更新日期:2021-09-03 类型:同步测试
一、单选题
-
1. 已知 ,它们的周长分别为30和15,且 ,则 的长为A、3 B、2 C、4 D、52. 如图,已知 ∽ ,则下列哪条线段与 的比等于相似比( ).
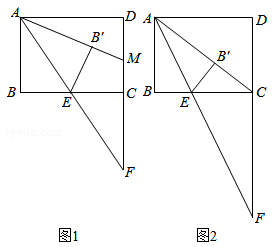
 A、 B、 C、 D、3. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( )
A、 B、 C、 D、3. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( ) A、2 B、4 C、6 D、84. 在四边形 中 ,对角线 与 交于 ,过点 作 的平行线,交 、 于 、 .若 , 与 的面积比为 ,则 的长是( )
A、2 B、4 C、6 D、84. 在四边形 中 ,对角线 与 交于 ,过点 作 的平行线,交 、 于 、 .若 , 与 的面积比为 ,则 的长是( ) A、 B、 C、 D、5. 如图,在 中, , ,则 的值是( )
A、 B、 C、 D、5. 如图,在 中, , ,则 的值是( )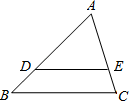 A、 B、1 C、 D、6. 如图,四边形 中, 为对角线 上一点,过点 作 ,交 于点 ,过点 作 ,交 于点 ,则下列所给的结论中,不一定正确的是( ).
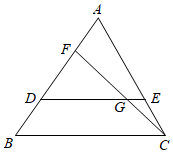
A、 B、1 C、 D、6. 如图,四边形 中, 为对角线 上一点,过点 作 ,交 于点 ,过点 作 ,交 于点 ,则下列所给的结论中,不一定正确的是( ).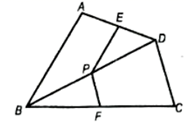 A、 B、 C、 D、7. 如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( )
A、 B、 C、 D、7. 如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( ) A、1:2 B、1:3 C、2:3 D、3:48. 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m , n),则大三角形中与之对应的顶点坐标为( )
A、1:2 B、1:3 C、2:3 D、3:48. 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m , n),则大三角形中与之对应的顶点坐标为( ) A、(﹣2m , ﹣2n) B、(2m , 2n) C、(﹣2n , ﹣2m) D、(2n , 2m)9. 如图,在平行四边形 中, , , 的面积为25,则四边形 的面积为( )
A、(﹣2m , ﹣2n) B、(2m , 2n) C、(﹣2n , ﹣2m) D、(2n , 2m)9. 如图,在平行四边形 中, , , 的面积为25,则四边形 的面积为( ) A、25 B、9 C、21 D、1610. 已知点 在第一象限,且 ,点 在 轴上,当 为直角三角形时,点 的坐标为( )A、 , 或 B、 , 或 C、 , 或 D、 , 或
A、25 B、9 C、21 D、1610. 已知点 在第一象限,且 ,点 在 轴上,当 为直角三角形时,点 的坐标为( )A、 , 或 B、 , 或 C、 , 或 D、 , 或二、填空题
-
11. 如图,在 中, , ,点P是 边的中点,点Q是 边上一动点,若 与 相似,则 的长为 .
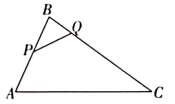 12. 如图,在 中,点D , E分别是 的中点, 与 相交于点F , 若 ,则 的长是 .
12. 如图,在 中,点D , E分别是 的中点, 与 相交于点F , 若 ,则 的长是 .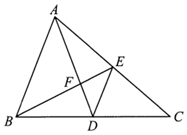 13. 如果两个相似三角形对应边上的中线之比为5:4.那么这两个三角形的周长之比为.14. 如图, 中, ,点D是边 上的一个动点(点D与点 不重合),若再增加一个条件,就能使 与 相似,则这个条件可以是(写出一个即可).
13. 如果两个相似三角形对应边上的中线之比为5:4.那么这两个三角形的周长之比为.14. 如图, 中, ,点D是边 上的一个动点(点D与点 不重合),若再增加一个条件,就能使 与 相似,则这个条件可以是(写出一个即可). 15. 如图,矩形ABCD中,AB=2,BC= ,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=.
15. 如图,矩形ABCD中,AB=2,BC= ,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=.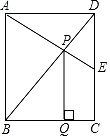 16. 如图,点C在 的内部,∠OCA=∠OCB , 与 互补,若 , ,则 .
16. 如图,点C在 的内部,∠OCA=∠OCB , 与 互补,若 , ,则 .
三、解答题
-
17. 如图,点D在△ABC的边AB上,AC2=AD•AB , 求证:△ACD∽△ABC .
 18. 如图,已知 ,求证: .
18. 如图,已知 ,求证: .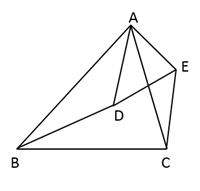 19. 已知:在 中,点D、E分别在AC、AB上,且满足 ,求证: .
19. 已知:在 中,点D、E分别在AC、AB上,且满足 ,求证: .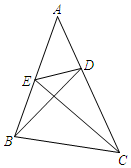 20. 如图,在 和 中,D、 分别是AB、 上一点, .
20. 如图,在 和 中,D、 分别是AB、 上一点, .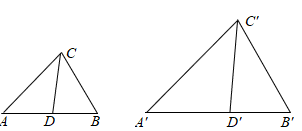 (1)、当 时,求证: 证明的途径可以用如框图表示,请填写其中的空格
(1)、当 时,求证: 证明的途径可以用如框图表示,请填写其中的空格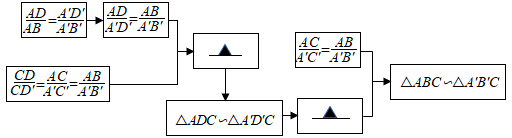 (2)、当 时,判断 与 是否相似,并说明理由
(2)、当 时,判断 与 是否相似,并说明理由