高中数学人教A版(2019)选择性必修一立体几何与空间向量章节检测
试卷更新日期:2021-09-03 类型:单元试卷
一、单选题
-
1. 设 , 是两个不同的平面, 是一条直线,以下结论正确的是( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则2. 如图, 为圆锥底面直径,点 是底面圆 上异于 的动点,已知 ,圆锥侧面展开图是圆心角为 的扇形,当 与 所成角为 时, 与 所成角为( )
 A、 B、 C、 D、3. 阿基米德是伟大的古希腊数学家,他和高斯、牛顿并列为世界三大数学家,他一生最为满意的一个数学发现就是“圆柱容球”定理,即圆柱容器里放了一个球,该球顶天立地,四周碰边(即球与圆柱形容器的底面和侧面都相切),球的体积是圆柱体积的三分之二,球的表面积也是圆柱表面积的三分之二.今有一“圆柱容球”模型,其圆柱表面积为 ,则该模型中球的体积为( )A、 B、4π C、 D、4. 如图所示,正方体 中,点 , , , , 分别为棱 , , , , 的中点.则下列叙述中正确的是( )
A、 B、 C、 D、3. 阿基米德是伟大的古希腊数学家,他和高斯、牛顿并列为世界三大数学家,他一生最为满意的一个数学发现就是“圆柱容球”定理,即圆柱容器里放了一个球,该球顶天立地,四周碰边(即球与圆柱形容器的底面和侧面都相切),球的体积是圆柱体积的三分之二,球的表面积也是圆柱表面积的三分之二.今有一“圆柱容球”模型,其圆柱表面积为 ,则该模型中球的体积为( )A、 B、4π C、 D、4. 如图所示,正方体 中,点 , , , , 分别为棱 , , , , 的中点.则下列叙述中正确的是( ) A、直线 平面 B、直线 平面 C、平面 平面 D、平面 平面5. 已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为 ,底面是边长为 的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )A、 B、 C、 D、6. 《九章算术》是中国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.例如,堑堵指底面为直角三角形且侧棱垂直于底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵 中, ,若 ,当阳马 的体积最大时,堑堵 中异面直线 所成角的大小是( )
A、直线 平面 B、直线 平面 C、平面 平面 D、平面 平面5. 已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为 ,底面是边长为 的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )A、 B、 C、 D、6. 《九章算术》是中国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.例如,堑堵指底面为直角三角形且侧棱垂直于底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵 中, ,若 ,当阳马 的体积最大时,堑堵 中异面直线 所成角的大小是( ) A、 B、 C、 D、7. 如图,在正方体ABCD﹣A1B1C1D1中,AM⊥平面A1BD,垂足为M,以下四个结论中正确的个数为( )
A、 B、 C、 D、7. 如图,在正方体ABCD﹣A1B1C1D1中,AM⊥平面A1BD,垂足为M,以下四个结论中正确的个数为( )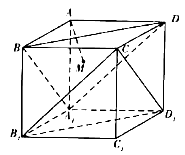
①AM垂直于平面CB1D1;②直线AM与BB1所成的角为45°;③AM的延长线过点C1;④直线AM与平面A1B1C1D1所成的角为60°
A、1 B、2 C、3 D、48. 如图,在矩形ABCD中,AB=2,AD=1,M为AB的中点,将△ADM沿DM翻折.在翻折过程中,当二面角A—BC—D的平面角最大时,其正切值为( ) A、 B、 C、
A、 B、 C、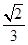 D、
D、
二、多选题
-
9. 在长方体 中, , , 分别是 上的动点,下列结论正确的是( )A、对于任意给定的点P,存在点 使得 B、对于任意给定的点Q,存在点 使得 C、当 时, D、当 时, 平面10. 在南方不少地区,经常看到人们头戴一种用木片、竹篾或苇蒿等材料制作的斗笠,用来遮阳或避雨,随着旅游和文化交流活动的开展,斗笠也逐渐成为一种时尚旅游产品.有一种外形为圆锥形的斗笠,称为“灯罩斗笠”,根据人的体型、高矮等制作成大小不一的型号供人选择使用,不同型号的斗笠大小经常用帽坡长(母线长)和帽底宽(底面圆直径长)两个指标进行衡量,现有一个“灯罩斗笠”,帽坡长20厘米,帽底宽 厘米,关于此斗笠,下面说法正确的是( )
 A、斗笠轴截面(过顶点和底面中心的截面图形)的顶角为 B、过斗笠顶点和斗笠侧面上任意两母线的截面三角形的最大面积为 平方厘米 C、若此斗笠顶点和底面圆上所有点都在同一个球上,则该球的表面积为 平方厘米 D、此斗笠放在平面上,可以盖住的球(保持斗笠不变形)的最大半径为 厘米11. 如图,在正方体 中, 是棱 上的动点.则下列结论正确的是( )
A、斗笠轴截面(过顶点和底面中心的截面图形)的顶角为 B、过斗笠顶点和斗笠侧面上任意两母线的截面三角形的最大面积为 平方厘米 C、若此斗笠顶点和底面圆上所有点都在同一个球上,则该球的表面积为 平方厘米 D、此斗笠放在平面上,可以盖住的球(保持斗笠不变形)的最大半径为 厘米11. 如图,在正方体 中, 是棱 上的动点.则下列结论正确的是( ) A、 平面 B、 C、直线 与 所成角的范围为 D、二面角 的大小为12. 如图,正方体 的棱长为1,动点E在线段 上,F、M分别是AD、CD的中点,则下列结论中正确的是( )
A、 平面 B、 C、直线 与 所成角的范围为 D、二面角 的大小为12. 如图,正方体 的棱长为1,动点E在线段 上,F、M分别是AD、CD的中点,则下列结论中正确的是( ) A、 B、 平面 C、存在点E,使得平面 平面 D、三棱锥 的体积为定值
A、 B、 平面 C、存在点E,使得平面 平面 D、三棱锥 的体积为定值三、填空题
-
13. 已知某圆锥底面圆的半径 ,侧面展开图是一个半圆,则此圆锥的体积为.14. 设 是不同的直线, 是不同的平面,则下列命题正确的是 .
①若 ,则 或 .
②若 ,则 或 .
③若 ,则 或 与 相交.
④若 ,则 或 .
15. 如图所示,平面 平面 , ,四边形 为正方形,且 ,则异面直线 与 所成角的余弦值为 . 16. 在《九章算术》中,将四个面都是直角三角形的四面体称之为鳖臑,在体积为 的鳖臑 中, 平面 ,且 , ,则该鳖臑外接球的表面积为 .
16. 在《九章算术》中,将四个面都是直角三角形的四面体称之为鳖臑,在体积为 的鳖臑 中, 平面 ,且 , ,则该鳖臑外接球的表面积为 .四、解答题
-
17. 如图,四棱锥 的底面 为直角梯形, ,且
为等边三角形,平面 平面 ;点 分别为 的中点.
 (1)、证明: 平面 ;(2)、求直线 与平面 所成角的正弦值.18. 已知多面体 中, 为正方形,平面 平面 , , , , , .
(1)、证明: 平面 ;(2)、求直线 与平面 所成角的正弦值.18. 已知多面体 中, 为正方形,平面 平面 , , , , , . (1)、证明: ;(2)、求平面 与平面 所成锐二面角的余弦值.19. 在图1所示的平面图形 中, 是边长为4的等边三角形, 是 的平分线,且 , 为 的中点,以 为折痕将 折起得到四棱锥 (如图2).
(1)、证明: ;(2)、求平面 与平面 所成锐二面角的余弦值.19. 在图1所示的平面图形 中, 是边长为4的等边三角形, 是 的平分线,且 , 为 的中点,以 为折痕将 折起得到四棱锥 (如图2). (1)、设平面 和 的交线为 ,在四棱雉 的棱 上求一点 ,使直线 ;(2)、若二面角 的大小为 ,求平面 和 所成锐二面角的余弦值.20. 如图,在三棱柱 中,平面 平面
(1)、设平面 和 的交线为 ,在四棱雉 的棱 上求一点 ,使直线 ;(2)、若二面角 的大小为 ,求平面 和 所成锐二面角的余弦值.20. 如图,在三棱柱 中,平面 平面 (1)、证明:平面 平面 ;(2)、若 与平面 所成角的正弦值为 ,求二面角 的余弦值.
(1)、证明:平面 平面 ;(2)、若 与平面 所成角的正弦值为 ,求二面角 的余弦值.

