浙江省绍兴市嵊州市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-09-03 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{1}{x - 1}$ 有意义，x的取值应满足（）

A、x≠1 B、x＝1 C、x＞1 D、x＜1

查看试题解析
2. 某种肺炎病毒的直径大约是0.00000013米，数据0.00000013用科学记数法可表示为（）

A、130×10^﹣9 B、1.3×10^﹣8 C、1.3×10^﹣7 D、0.13×10^﹣6

查看试题解析
3. 下列运算正确的是（　　）

A、a³+a³=2a⁶ B、（x²）³=x⁵ C、2a⁶÷a³=2a² D、x³•x²=x⁵

查看试题解析
4. 如图，平行线AB ， CD被直线AE所截，∠1＝80°，则∠2的度数是（）

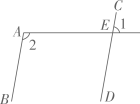A、80° B、90° C、100° D、110°

查看试题解析
5. 小林家今年1―5月份的用电量情况如图所示，由图可知，相邻的两个月中，用电量变化最大的是（）

A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月

查看试题解析
6. 下面的计算过程中，从哪一步开始出现错误（）.

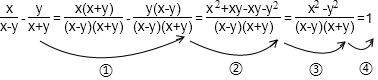A、① B、② C、③ D、④

查看试题解析
7. 关于x的分式方程 $\frac{x - 3}{x - 1} = \frac{m}{x - 1}$ 有增根，则m的值是（）

A、﹣2 B、3 C、﹣3 D、2

查看试题解析
8. 用加减消元法解二元一次方程组 ${\begin{matrix} x + 3 y = 4 ① \\ 2 x - y = 1 ② \end{matrix}$ 时，下列方法中无法消元的是（）

A、①×2﹣② B、②×（﹣3）﹣① C、①×（﹣2）+② D、①﹣②×3

查看试题解析
9. 对于1到9的四个整数a，b，c，n（四个数中n最大），我们规定符号（ $\bar{a b c}$ ）_n的意义是：（ $\bar{a b c}$ ）_n＝a•n²+b•n+c•n⁰.例如：（ $\bar{245}$ ）₇＝2×7²+4×7+5×7⁰＝131，（ $\bar{245}$ ）₆＝2×6²+4×6+5×6⁰＝101.（ $\bar{234}$ ）_b+1﹣（ $\bar{234}$ ）_b﹣1＝70，则（ $\bar{234}$ ）_b的值为（）

A、45 B、48 C、153 D、156

查看试题解析
10. 如图，将长方形纸片沿EB，CF折叠成图1，使AB，CD在同一直线上，再沿BF折叠成图2，使点D落在点D'处，BD'交CF于点P，若∠CEB＝37°，则∠CPB的度数为（）

A、110° B、111° C、112° D、113°

查看试题解析

二、填空题

11. 计算：（4a²﹣7a）÷7a＝.

查看试题解析
12. 若x²﹣10x+m是一个完全平方式，则m的值为 .

查看试题解析
13. 已知二元一次方程3x+2y＝10，用含x的代数式表示y，则y＝.

查看试题解析
14. 已知a﹣5b＝0，则分式 $\frac{a - 2 b}{b}$ 的值为 .

查看试题解析
15. 将40个数据分成6组，第一组到第四组的频数分别为9，5，8，6，第六组的频率是0.1，则第五组的频率是 .

查看试题解析
16. 关于x，y的二元一次方程组 ${\begin{matrix} x + y = 9 k \\ x - y = 5 k \end{matrix}$ 的解也是二元一次方程2x+y＝16的解，则k的值为 .

查看试题解析
17. 若 $4 x - 3 y - 3 = 0$ ，则10^4x÷10^3y=.

查看试题解析
18. 如图，长方形ABCD的长AD为6，宽AB为4，将这个长方形向上平移2个单位，再向右平移2个单位，得到长方形EFGH，则阴影部分的面积为 .

查看试题解析
19. 如图，AB∥CD，∠BOC＝100°，BE，CF分别平分∠ABO，∠OCD，则∠2﹣∠1＝.

查看试题解析
20. 将12张长为a，宽为b（a＞b）的小长方形纸片，按如图方式不重叠地放在大长方形ABCD内，未被覆盖的部分用阴影表示，若阴影部分的面积是大长方形面积的 $\frac{1}{3}$ ，则小长方形纸片的长a与宽b的比值为 .

查看试题解析

三、解答题

21. 计算：

(1)、（ $\sqrt{3}$ ）⁰+（ $\frac{1}{2}$ ）^﹣2；

(2)、（x+y）²﹣（x﹣y）（x+y）.

查看试题解析
22. 解下列方程（组）：

(1)、 ${\begin{matrix} 3 x + 2 y = 13 \\ 3 x - 2 y = 5 \end{matrix}$ ；

(2)、 $\frac{6}{1 - x^{2}} = \frac{3}{1 - x}$ .

查看试题解析
23. 分解因式：

(1)、25a²﹣4；

(2)、3ax²﹣6axy+3ay².

查看试题解析

24. 某市在开展线上教学活动期间，为更好地组织初中学生居家体育锻炼，随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查（每人必须且只选其中一项），得到如下两幅不完整的统计图表，请根据图表信息回答下列问题：

类别	项目	人数
A	跳绳	59
B	健身操	▲
C	俯卧撑	31
D	开合跳	▲
E	其它	22

(1)、求参与问卷调查的学生总人数.

(2)、在参与问卷调查的学生中，最喜爱“开合跳”的学生有多少人？

(3)、该市共有初中学生约8000人，估算该市初中学生中最喜爱“健身操”的人数.

查看试题解析

25. 如图，D是BC上一点，DE∥AB，交AC于点E.

(1)、若∠1＝∠A，判断DF与AC是否平行，并说明理由；

(2)、若DF∥AC，∠B+∠C＝120°，求∠1的度数.

查看试题解析
26. 2021年是中国共产党成立100周年，为了让学生重温红色经典，传承革命精神，学校组织193名学生乘车去参观距学校6km的红色基地.现已预备了大客车和小客车共8辆，其中大客车每辆可坐51人，小客车每辆可坐8人，刚好都坐满.

(1)、学校预备了几辆大客车，几辆小客车？

(2)、为磨练自己意志，一部分学生改为步行前往红色基地，其余学生乘大客车出发，已知大客车速度是步行速度的6倍，他们同时出发，步行的学生晚50分钟到达基地，求步行的速度.

查看试题解析
27. 如图，直线AB、CD被DQ所截，AB∥CD，∠BDC＝50°，点E是直线CD上的动点（点E与点D不重合），连结BE，作∠ABE的角平分线交直线CD于点F.

(1)、如图1，点E在点D左侧，若∠DBE＝20°，求∠EBF的度数.

(2)、①如图2，点E在点D左侧，BG是∠ABF的角平分线，求∠FBG的度数.
②若F'是BF反向延长线上的一点，求∠F'BG的度数.

查看试题解析