四川省遂宁市城区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-09-03 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $x = 2$ 是关于 $x$ 的一元一次方程 $a x + 1 = 5$ 的解，那么 $a$ 的值为（）

A、 $- 3$ B、 $- 2$ C、 $2$ D、 $3$

查看试题解析
2. 下列图案中，是轴对称图形但不是中心对称图形的是（）

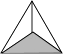A、 B、 C、 D、

查看试题解析
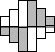3. 已知三角形的两边长分别是4和9，则此三角形第三条边的长可能是（）

A、3 B、4 C、6 D、15

查看试题解析
4. 已知等式 $3 a = 2 b - 4$ ，则下列等式中不成立的是（）

A、 $3 a - 2 b = - 4$ B、 $3 a - 1 = 2 b - 5$ C、 $3 a c = 2 b c - 4$ D、 $3 a (c + 1) = (2 b - 4) (c + 1)$

查看试题解析
5. 若m＞n，则下列各式不一定成立的是（）

A、2m＞m＋n B、1－m＜1－n C、 $m^{2} > n^{2}$ D、 $2 m + 1 > 2 n - 3$

查看试题解析
6. 若一个正多边形的一个内角为 $144 °$ ，则这个图形为正（）边形

A、八 B、九 C、七 D、十

查看试题解析
7. 小飞家房屋装修时，选中了一种漂亮的正八边形地砖，建材店老板告诉她，只用一种八边形地砖是不能铺满地面的，但可以与另外一种形状的地砖混合使用，你认为要使地面铺满，小飞应选择另一种（）形状的地砖

A、正三角形 B、正方形 C、正五边形 D、正六边形

查看试题解析
8. 下列说法中错误的是（）

A、三角形的一个外角大于任何一个内角 B、有一个内角是直角的三角形是直角三角形 C、任意三角形的外角和都是 $360^{\circ}$ D、三角形的中线、角平分线，高线都是线段

查看试题解析
9. 若 $2 x + 5 y - 3 z = 2$ ， $3 x + 8 z = 3$ ，则x＋y＋z的值等于（）

A、0 B、2 C、1 D、无法求出

查看试题解析
10. 若方程组 ${\begin{array}{l} 2 x + y = 3 \\ (k - 1) x + (k + 1) y = 4 \end{array}$ 的解中，x与y相等，则k的值是（）

A、3 B、2 C、0 D、10

查看试题解析
11. 关于 $x$ 的不等式 $x - 2 m < 0$ 的正整数解是1、2、3，那么m的取值范围是（）

A、 $\frac{3}{2} < m \leq 2$ B、 $\frac{3}{2} \leq m \leq 2$ C、 $\frac{3}{2} \leq m < 2$ D、 $\frac{3}{2} < m < 2$

查看试题解析
12. 如图所示，将边长为 $8 cm$ 的正方形 $A B C D$ 先向上平移 $4 cm$ ，再向右平移 $2 cm$ ，得到正方形 $A^{'} B^{'} C^{'} D^{'}$ ，此时阴影部分的面积为（）

A、 $24 {cm}^{2}$ B、 $26 {cm}^{2}$ C、 $18 {cm}^{2}$ D、 $20 {cm}^{2}$

查看试题解析
13. 如图，将△ABC绕着点B逆时针旋转45°后得到△A'BC′，若∠A＝120°，∠C＝35°，则∠A'BC的度数为（）

A、20° B、25° C、30° D、35°

查看试题解析
14. 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重.问：每只雀、燕的重量各为多少?设一只雀的重量为x斤，一只燕的重量为y斤，则可列方程组为（）

A、 ${\begin{cases} 5 x + 6 y = 1 \\ 5 x - y = 6 y - x \end{cases}$ B、 ${\begin{cases} 6 x + 5 y = 1 \\ 5 x + y = 6 y + x \end{cases}$ C、 ${\begin{cases} 5 x + 6 y = 1 \\ 4 x + y = 5 y + x \end{cases}$ D、 ${\begin{cases} 6 x + 5 y = 1 \\ 4 x - y = 5 y - x \end{cases}$

查看试题解析
15. 甲、乙两位同学在解关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} 2 x + a y = 1 \\ b x - y = 2 \end{array}$ 时，甲同学看错 $a$ 得到方程组的解为 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ ，乙同学看错 $b$ 得到方程组的解为 ${\begin{array}{l} x = 2 \\ y = - 3 \end{array}$ ，则 $x + y$ 的值为（）

A、 $0$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、 $\frac{5}{4}$

查看试题解析
16. 现规定一种运算： $a * b = a b + a - b$ ，其中 $a ， b$ 为常数，若 $2 * 3 + m * 1 = 6$ ，则不等式 $\frac{3 x + 2}{2} < m$ 的解集是（）

A、 $x < - 2$ B、 $x < - 1$ C、 $x < 0$ D、 $x > 2$

查看试题解析
17. 已知等腰三角形的两边长分别为a、b，且a、b满足 $| 2 a - b - 1 | + {(b - a - 2)}^{2} = 0$ ，则此等腰三角的周长是（）

A、8 B、11 C、13 D、11或13

查看试题解析
18. 下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有1个空心小圆圈，第②个图形中一共有6个空心小圆圈，第③个图形中一共有13个空心小圆圈，…，按此规律排列，则第⑥个图形中空心圆圈的个数为（）

A、46 B、48 C、56 D、58

查看试题解析

二、填空题

19. 关于x的方程（k-4）x^|k|-3+1=0是一元一次方程，则k的值是.

查看试题解析
20. 关于x，y的二元一次方程2x＋3y＝12的非负整数解有组.

查看试题解析
21. 三元一次方程组 $\{\begin{matrix} x + y = 5 \\ y + z = 9 \\ z + x = 8 \end{matrix}$ 的解是

查看试题解析
22. 若关于x，y的二元一次方程组 ${\begin{array}{l} 2 x + y = - 4 m + 5 \\ x + 2 y = m + 4 \end{array}$ 的解满足 ${\begin{array}{l} x - y > - 6 \\ x + y < 8 \end{array}$ ，求m的取值范围.

查看试题解析
23. 如图所示，∠1+∠2+∠3+∠4+∠5+∠6=度．

查看试题解析
24. 在直角三角形 $A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点 $D$ ， $B E$ 平分 $∠ A B C$ 交 $A C$ 于点 $E$ ， $A D$ 、 $B E$ 相交于点 $F$ ，过点 $D$ 作 $D G / / A B$ ，过点 $B$ 作 $B G ⊥ D G$ 交 $D G$ 于点 $G$ .下列结论：① $∠ A F B = 135 °$ ；② $∠ B D G = 2 ∠ C B E$ ；③ $B C$ 平分 $∠ A B G$ ；④ $∠ B E C = ∠ F B G$ .其中正确的是.

查看试题解析

三、解答题

25.

(1)、解方程：y– $\frac{y - 1}{2} = 2 - \frac{y + 2}{5}$ .

(2)、解方程组： ${\begin{array}{l} x - 2 y = 3 \\ 12 x + 7 y = 5 \end{array}$

查看试题解析
26. 解不等式组： ${\begin{array}{l} \frac{x - 3}{2} + 3 \geq 4 \\ 1 - 3 (x - 1) < 8 - x \end{array}$ 并将其解集在数轴上表示出来；

查看试题解析
27. 如图，在8×8的正方形网格中，每个小正方形的边长均为1个单位，△ABC的三个顶点都在格点上.

（1）在网格中画出△ABC关于直线MN的对称图形△A₁B₁C₁；
（2）在网格中画出△ABC向下平移3个单位长度，再向右平移3得到的△A₂B₂C₂；
（3）在网格中画出△ABC绕点C逆时针旋转90°后的图形△A₃B₃C₃.

查看试题解析
28. 如图，△ABC中，AD平分∠BAC，P为AD延长线上一点，PE⊥BC于E，已知∠ACB＝80°，∠B＝24°，求∠P的度数.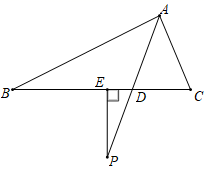

查看试题解析
29. 我们知道，任意一个正整数x都可以进行这样的分解：x=m×n（m，n是正整数，且m≤n），在x的所有这种分解中，如果m，n两因数之差的绝对值最小，我们就称m×n是x的最佳分解．并规定：f（x）= $\frac{m}{n}$ .
例如：18可以分解成1×18，2×9或3×6，因为18-1>9-2>6-3，所以3×6是18的最佳分解，所以f（18）= $\frac{3}{6}$ = $\frac{1}{2}$ ．

(1)、填空：f（6）= ， f（9）=；

(2)、一个两位正整数t（t=10a+b，1≤a≤b≤9，a，b为正整数），交换其个位上的数字与十位上的数字，得到的新数减去原数所得的差为54，求出所有满足条件的两位正整数，并求f（t）的最大值．

查看试题解析
30. 2018年宜宾市创建全国文明城市的过程中，某小区决定购买文明用语提示牌和文明信息公示栏.若购买2个提示牌和3个公示栏需要510元；购买3个提示牌和5个公示栏需要840元.

(1)、求提示牌和公示栏的单价各是多少元？

(2)、若该小区购买提示牌和公示栏共50个，要求购买公示栏至少12个，且总费用不超过3200元.请你列举出所有购买方案，并指出哪种方案费用最少，最少费用为多少元？

查看试题解析
31. 如图（1），直角△ABC与直角△BCD中∠ACB＝90°，∠A＝30°，∠D＝45°，固定△BCD，将△ABC绕点C按顺时针方向旋转一个大小为 $α$ 的角（0°＜ $α$ ≤180°）得△ACB′.

(1)、在旋转过程中，当B'C⊥BD时， $α$ ＝°；

(2)、如图（2），旋转过程中，若边AB'与边BC相交于点E，与边BD相交于点F，连接AD，设∠DAB'＝ $θ$ ，∠BCB'＝ $β$ ，∠ADB＝ $γ$ ，试探究 $θ$ ＋ $β$ ＋ $γ$ 的值是否发生变化，若不变请求出这个值，若变化，请说明理由；

(3)、在旋转过程中，当AB'与△BCD的边垂直时，直接写出 $α$ 的度数.

查看试题解析