四川省广元市青川县2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-09-03 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列说法中:
①因为对顶角相等,所以相等的两个角是对顶角;
②在平面内,不相交的两条直线叫做平行线;
③平面内,过一点有且只有一条直线与已知直线垂直;
正确的有( ).
A、 个 B、 个 C、 个 D、 个3. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、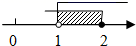 D、
D、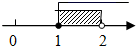 4. 下列方程中,是二元一次方程的是( )A、x2+x=1 B、2x﹣3y=5 C、xy=3 D、3x﹣y=2z5. 已知实数 , 满足 ,则 等于( )A、3 B、-3 C、1 D、-16. 某养鸭场有若干只鸭,某天捉到30只全部做上标记,又过了一段时间,捉到50只,其中有2只有标记,那么估计该养鸭场有鸭子( )A、500只 B、650只 C、750只 D、900只7. 如图,直线 , 被两条直线所截,若 , , ,则 的读数为( )
4. 下列方程中,是二元一次方程的是( )A、x2+x=1 B、2x﹣3y=5 C、xy=3 D、3x﹣y=2z5. 已知实数 , 满足 ,则 等于( )A、3 B、-3 C、1 D、-16. 某养鸭场有若干只鸭,某天捉到30只全部做上标记,又过了一段时间,捉到50只,其中有2只有标记,那么估计该养鸭场有鸭子( )A、500只 B、650只 C、750只 D、900只7. 如图,直线 , 被两条直线所截,若 , , ,则 的读数为( )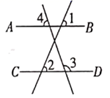 A、 B、 C、 D、8. 《孙子算经》是我国古代一部较为普及的算书,其中记载了一道题,大意是:100个和尚分100个馒头,大和尚1人分3个馒头,小和尚3人分1个馒头,问大、小和尚各有多少人.若设大和尚有x人,小和尚有y人,则可列出方程组( )A、 B、 C、 D、9. 已知点P(x,y),且xy>0,点P到x轴的距离是3个单位,到y轴的距离是2个单位,则点P的坐标是( )A、 B、 C、 或 D、10. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A、 B、 C、 D、8. 《孙子算经》是我国古代一部较为普及的算书,其中记载了一道题,大意是:100个和尚分100个馒头,大和尚1人分3个馒头,小和尚3人分1个馒头,问大、小和尚各有多少人.若设大和尚有x人,小和尚有y人,则可列出方程组( )A、 B、 C、 D、9. 已知点P(x,y),且xy>0,点P到x轴的距离是3个单位,到y轴的距离是2个单位,则点P的坐标是( )A、 B、 C、 或 D、10. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )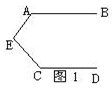


 A、、1个 B、2个 C、3个 D、4个
A、、1个 B、2个 C、3个 D、4个二、填空题
-
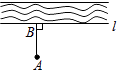
11. 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.理由是 .
 12. 如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是.
12. 如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是. 13. 若-2xm-ny2与3x4y2m+n是同类项,则m-3n的立方根是.14. 定义运算“☆”,规定x☆y=ax+by,其中a,b为常数,且1☆2=5,2☆3=6,则1☆3=.15. 若不等式组 的解集是 ,则 .16. 在平面直角坐标系 中,对于点 我们把 叫做点P的伴随点,已知 的伴随点为 ,点 的伴随点为 ,点 的伴随点为 ,这样依次得到 ,若点 的坐标为 ,则点 的坐标为
13. 若-2xm-ny2与3x4y2m+n是同类项,则m-3n的立方根是.14. 定义运算“☆”,规定x☆y=ax+by,其中a,b为常数,且1☆2=5,2☆3=6,则1☆3=.15. 若不等式组 的解集是 ,则 .16. 在平面直角坐标系 中,对于点 我们把 叫做点P的伴随点,已知 的伴随点为 ,点 的伴随点为 ,点 的伴随点为 ,这样依次得到 ,若点 的坐标为 ,则点 的坐标为三、解答题
-
17. 计算:(1)、(2)、18.(1)、解方程组:(2)、解不等式2x-3< ,并把解集在数轴上表示出来19. 已知a是不等式组 的整数解,x,y满足方程组 ,求(x+y)(x2-xy+y2)的值.20. 在平面直角坐标系中的位置如图所示.
 (1)、分别写出下列各点的坐标: ; ; ;(2)、请将 向右平移4个单位长度,再向上平移2个单位长度,请画出平移后的 .(3)、若点 是 内部一点,则 内部的对应点 的坐标为 ;(4)、求 的面积.21. 已知∠B=∠BGD,∠BGC=∠F.求证:∠B+∠F=180°.
(1)、分别写出下列各点的坐标: ; ; ;(2)、请将 向右平移4个单位长度,再向上平移2个单位长度,请画出平移后的 .(3)、若点 是 内部一点,则 内部的对应点 的坐标为 ;(4)、求 的面积.21. 已知∠B=∠BGD,∠BGC=∠F.求证:∠B+∠F=180°.
证明:∵∠B=∠BGD(已知)
∴_▲_//CD ( )
∵∠BGC=∠F(已知)
∴CD// _▲_( )
∴_▲_// _▲__(平行于同一直线的两直线平行)
∴∠B+ _▲_=180°( ).
22. 为传承中华优秀传统文化,某校团委组织了一次全校2800名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行统计,制成不完整的统计图表:成绩x(分)
划记
频数(人)
50≤x<60
正正
10
60≤x<70
m
30
70≤x<80
正正正正正正正正
40
80≤x<90
正正正正正正正正正正正正正正
n
90≤x<100
正正正正正正正正正正
50

根据所给信息,解答下列问题:
(1)、在这个问题中,有以下说法:①2800名学生是总体;②200名学生的成绩是总体的一个样本;③每名学生是总体的一个个体;④样本容量是200;⑤以上调查是全面调查.其中正确的说法是 (填序号)(2)、统计表中m= , n=;(3)、补全频数分布直方图;(4)、若成绩在90分以上(包括90分)为优等,请你估计该校参加本次比赛的2800名学生中成绩是优等的约为多少人?23. 解关于x、y的方程组 时,甲正确地解得方程组的解为 ,乙因为把c抄错了,在计算无误的情况下解得方程组的解为 ,求a、b、c的值.24. 为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.(1)、改扩建1所A类学校和1所B类学校所需资金分别是多少万元?(2)、该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担,若国家财政拨付资金不超过11800万元,地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校改扩建资金分别为每所300万元和500万元,请问共有哪几种改扩建方案?
