四川省成都市龙泉驿区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期：2021-09-03 类型：期末考试
一、单选题
-
1. 下列四个常见的手机APP图标中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列运算正确的是（ ）A、（a3）4＝a7 B、（﹣2a2b）3＝﹣6a6b3 C、（2a+b）2＝4a2+b2 D、a8÷a2＝a63. 如图，l1∥l2 ， 如果∠1＝76°，那么∠2的度数为（ ）
A、14° B、76° C、84° D、104°4. 下列说法正确的是（ ）A、袋中有形状、大小、质地完全一样的5个红球和1个白球，从中随机抽出一个球，一定是红球 B、天气预报“明天降水概率10%”，是指明天有10%的时间会下雨 C、某地发行一种福利彩票，中奖率是千分之一，那么，买这种彩票1000张，一定会中奖 D、连续掷一枚均匀硬币，若5次都是正面朝上，则第六次仍然可能正面朝上5. 下列乘法公式运用正确的是（ ）A、（a+b）（b﹣a）＝a2﹣b2 B、（﹣m+1）（﹣m﹣1）＝m2﹣1 C、（2x﹣1）2＝2x2+4x﹣1 D、（a+1）2＝a2+16. 如图，点A，D，C，F在同一条直线上，AD＝CF，∠F＝∠ACB，再补充下列一个条件，不能证明△ABC≌△DEF的是（ ）
A、BC＝EF B、AB∥DE C、AB＝DE D、∠B＝∠E7. 等腰三角形的两边分别为5和10，则它的周长是 （ ）
A、20 B、15 C、25 D、20或258. 如图，在△ABC中，线段AB的垂直平分线与AC相交于点D，连接BD，边AC的长为12cm，边BC的长为7cm，则△BCD的周长为（ ）
A、18cm B、19cm C、20cm D、21cm9. 如图，现有若干个边长相等的小等边三角形组成的图形，其中已经涂黑了3个小三角形（阴影部分表示），在空白的三角形中只涂黑一个小三角形，使整个图案成轴对称图形的概率是（ ）
A、 B、 C、 D、10. 公式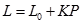
表示当重力为P时的物体作用在弹簧上时弹簧的长度. 
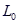表示弹簧的初始长度，用厘米（cm）表示，K表示单位重力物体作用在弹簧上时弹簧的长度，用厘米（cm）表示．下面给出的四个公式中，表明这是一个短而硬的弹簧的是（ ） A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P二、填空题
-
11. 关于x的二次多项式x2+6x+m恰好是另一个多项式的平方，则常数项m＝ ．12. 等腰三角形的一个底角为 ，则它的顶角的度数为 ．
13. 如图，将直尺与30°角的三角尺叠放在一起，若 ，则 .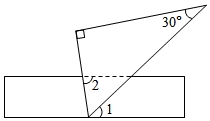
14. 如图，在△ABC中，点D是BC边的中点，点E是AC边的中点，连接AD，DE，若S阴影＝1，则S△ABC＝.
15. 一个不透明的盒子中有颜色不同，形状相同的小球，其中红球有10个，黑球有8个，现随机从中摸出一个，则摸到黑球的概率为 .16. 已知等腰三角形两边的长为a，b，且满足|a﹣4|+（b﹣5）2＝0.则这个等腰三角形的周长为 .17. 如图所示，AD、CE、BF是△ABC的三条高，AB＝6，BC＝5，AD＝4，则CE＝ ．
18. 如图，在△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 MN的长为半径画弧，两弧交于P，连接AP并延长交BC于点D，已知CD＝5，则DB＝.
19. 如图，在四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC，CD上分别找一点M，N，使三角形AMN周长最小时，则∠MAN的度数为.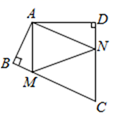
三、解答题
-
20. 计算：(1)、（﹣2）3+（2020+π）0﹣|﹣3|；(2)、（﹣3a2）3﹣4a2•a4+5a9÷a3.21. 先化简，再求值：（2a+b）（2a﹣b）﹣3（a+b）2+4b2 ， 其中a＝2，b＝﹣1.22. 已知∠α，线段m，n，求作：△ABC，使得∠A＝∠α，AB＝m，AC＝n.（要求：用直尺和圆规作图，保留作图痕迹，不写作法及证明，必须作答）
23. 新能源纯电动汽车的不断普及让很多人感受到了它的好处，其中最重要的一点就是对环境的保护，如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量y（千瓦时）与已行驶路程x（千米）之间关系的图象.
(1)、图中点A表示的实际意义是什么？(2)、当0≤x≤150时，行驶1千米的平均耗电量多少？(3)、求行驶多少千米时，剩余电量降至15千瓦时.24. 如图，点A，B，C，D在一条直线上，AB＝CD，CE∥BF，CE＝BF，求证：AE∥DF.（每行都要写理由）
25. 如图，在△ABC中，AB＝AC，点D，E分别是BC，AC上的点，且BD＝CE，连接AD，DE，若∠ADE＝∠B.求证：AD＝DE.（每行都要写理由）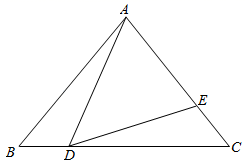
26. 如图，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一条直线上，连接BE.
(1)、求证：AD＝BE；(2)、求∠AEB的度数.27. 如图1，点P、Q分别是等边 上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M.
(1)、求证： ；(2)、当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数.(3)、如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数.28. 如图1，已知△ABC和△DEC都是等腰直角三角形，C为它们的公共直角顶点，D、E分别在BC、AC边上，点F是AD的中点，连接CF.
(1)、求证：△ACD≌△BCE；(2)、判断BE与CF的数量关系和位置关系，并说明理由；(3)、如图2，把△DEC绕点C顺时针旋转α角（0＜α＜90°），即∠BCD＝∠ACE＝α，点F是AD的中点，其他条件不变，判断BE与CF的关系是否不变？若不变，请说明理由；若要变，请求出相应的正确结论.