广西壮族自治区来宾市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-09-03 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示，直线AB，CD相交于点O，已知 $∠ A O D = 140 °$ ，则 $∠ B O C$ 的大小为（）

A、 $20 °$ B、 $40 °$ C、 $70 °$ D、 $140 °$

查看试题解析
2. 下列属于二元一次方程组的是（）

A、 ${\begin{array}{l} x - y = 3 \\ y - 3 x = 7 \end{array}$ B、 ${\begin{array}{l} x + 2 y = 5 \\ y + 3 z = 7 \end{array}$ C、 ${\begin{array}{l} x - y = 4 x y \\ x - 2 y = 1 \end{array}$ D、 ${\begin{array}{l} x + y = 4 \\ x^{2} = 4 \end{array}$

查看试题解析
3. 下列各图中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算中，正确的是（）

A、 $a \cdot a^{3} = a^{3}$ B、 $4 x^{2} \cdot 3 x^{3} = 12 x^{6}$ C、 $a^{3} + a^{3} = 2 a^{3}$ D、 ${(- 2 x y)}^{3} = 6 x^{3} y^{3}$

查看试题解析

5. 某区学生在“垃圾分类知识”线上答题活动中，甲、乙、丙、丁四所学校参加线上答题的人数相同，四所学校答题所得分数的平均数和方差如下表：

	甲	乙	丙	丁
平均数	85	85	85	85
方差	0.025	0.041	0.038	0.028

则这四所学校成绩发挥最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 如图，将 $△ A B C$ 绕着顶点C顺时针旋转30°，点B落在 $B^{'}$ 处，点A落在 $A^{'}$ 处.若 $A C ⊥ A^{'} B^{'}$ ，则 $∠ B A C$ 的度数是（）

A、50° B、60° C、70° D、80°

查看试题解析
7. 如图，能判定 $E C / / A D$ 的条件是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ 5 = ∠ 6$ D、 $∠ 2 = ∠ 3$

查看试题解析
8. 如图，将一块含30°角的直角三角板放置在平行线a，b之间，且较长直角边靠在直线b上，然后将三角板绕着顶点A逆时针旋转25°后另一个顶点B恰好落在直线b上，这时直角边BC与直线a上所构成的角 $∠ 1$ 等于（）

A、55° B、60° C、65° D、70°

查看试题解析
9. 将一副三角板按如图方式摆放，且 $∠ 1$ 的度数比 $∠ 2$ 的度数多10°，若设 $∠ 1 = x °$ ， $∠ 2 = y °$ ，则可得方程组为（）

A、 ${\begin{array}{l} x = y - 10 \\ x + y = 180 \end{array}$ B、 ${\begin{array}{l} x = y + 10 \\ x + y = 90 \end{array}$ C、 ${\begin{array}{l} x = y + 10 \\ x + y = 180 \end{array}$ D、 ${\begin{array}{l} x = y - 10 \\ x + y = 90 \end{array}$

查看试题解析
10. 将长方形纸片ABCD按如图所示方式折叠，使得 $∠ A^{'} E B^{'} = 40 °$ ，其中EF，EG为折痕，则 $∠ A E F + ∠ B E G$ 的度数为（）

A、40° B、70° C、80° D、140°

查看试题解析
11. 下列因式分解正确的是（）

A、 $x^{2} - 2 x + 4 = {(x - 2)}^{2}$ B、 $4 x^{2} - y^{2} = (4 x + y) (4 x - y)$ C、 $x^{2} - \frac{1}{2} x + \frac{1}{16} = {(x - \frac{1}{4})}^{2}$ D、 $a^{4} b - 6 a^{3} b + 9 a^{2} b = a^{2} b (a^{2} - 6 a + 9)$

查看试题解析
12. 有两个正方形 $A ， B$ ，现将 $B$ 放在 $A$ 的内部得图甲，将 $A ， B$ 并列放置后构造新的正方形得图乙，若图甲和图乙中阴影部分的面积分别为3和16，则正方形 $A ， B$ 的面积之和为（）

A、13 B、11 C、19 D、21

查看试题解析

二、填空题

13. 计算： ${(- 3 x)}^{3} =$ .

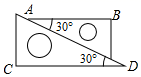
查看试题解析
14. 如图，将两个含角 $30 °$ 的直角三角板的最长边靠在一起滑动，可知直角 $A B / / C D$ 边，依据是.

查看试题解析
15. 有一组数据a，b，c，d，e，f，设这组数据的平均数是m，将这组数据改变为 $a + 3$ ，b，c，d，e， $f - 1$ ，设改变后的这组数据的平均数是n，则mn（填“>”，或“<”，或“=”）

查看试题解析
16. 分解因式： $a b^{2} - 36 a =$ .

查看试题解析
17. 已知方程组 ${\begin{array}{l} 5 x + y = 3 \\ a x + 5 y = 4 \end{array}$ 与 ${\begin{array}{l} x - 2 y = 5 \\ 5 x + b y = 1 \end{array}$ 有相同的解，则 $a^{2} - 2 a b + b^{2} =$ .

查看试题解析
18. 有如图所示的四个长方形，用这四个长方形拼成一个长为 $a + b$ 的长方形，使其面积等于原来4个长方形的面积之和，则拼成的长方形的宽是.

查看试题解析

三、解答题

19.

(1)、解方程组： ${\begin{array}{l} x + y = - 1 \\ 4 x + y = 5 \end{array}$ ；

(2)、分解因式： $- 4 x^{2} + 8 x - 4$ .

查看试题解析
20. 先化简，再求值：（x+1）（x﹣1）+x（2﹣x），其中x= $\frac{1}{2}$ .

查看试题解析
21. 如图，已知 $△ A B C$ 和直线MN.

（ 1 ）画出 $△ A B C$ 关于直线MN成轴对称的 $△ A_{1} B_{1} C_{1}$ ；

（ 2 ）画出 $△ A B C$ 绕它的顶点B按逆时针方向旋转90°后的图形 $△ A_{2} B_{2} C_{2}$ .

查看试题解析

22. 今年是中国共产党成立100周年，某中学在全校学生中开展“党史知识竞赛”活动，从中随机抽取九年级25名学生的成绩（分数为正整数，满分100分）：

90，74，88，65，98，75，81，44，85，70，55，80，95，

88，72，87，60，56，76，66，78，72，82，63，100.

并制作如下的不完全统计表：

成绩x/分	$x < 60$		$60 \leq x < 75$		$75 \leq x < 90$	$x \geq 90$
人数	$a$		8		10	$b$
平均数		中位数		方差
76		$c$		190.88

请根据上述数据完成下列问题：

(1)、将统计表补充完整：

a =

，

b =

，

c =

；

(2)、该校九年级有1000名学生，请估计该校九年级学生中成绩达到90分及以上的人数；

(3)、若随机抽取25名八年级学生的成绩进行统计，平均数为76分，中位数为80分，方差为102.5，请从平均数、中位数和方差三个方面对八年级和九年级的成绩进行评价.

查看试题解析

23. 如图，直线 $A C / / B D$ ，BC平分 $∠ A B D$ ， $D E ⊥ B C$ ，垂足为点E， $∠ E D B = 50 °$ ，求 $∠ B A C$ 的度数.

查看试题解析
24. 某市的出租车收费标准如下：起步价所允许行驶的最远路程为3千米，超过3千米的部分按每千米另收费.
甲说：“我乘出租车走了10千米，付车费21.2元.

乙说：“我乘出租车走了14千米，付车费27.6元.

问：

(1)、出租车起步价是多少元？超过3千米的部分每千米收费多少元？

(2)、小张乘出租车走了5.5千米，应付车费多少元？

查看试题解析
25. 阅读下列材料：
我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法，配方法是一种重要的解决数学问题的方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式的最大值、最小值等.

例如： $x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 4 = {(x + 1)}^{2} - 2^{2} = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$ ；

$x^{2} - 10 x + 30 = x^{2} - 10 x + 25 + 5 = (x^{2} - 10 x + 25) + 5 = {(x - 5)}^{2} + 5$ ，

因为 ${(x - 5)}^{2} \geq 0$ ，即 ${(x - 5)}^{2}$ 的最小值是0，所以 $x^{2} - 10 x + 30$ 的最小值是5.

根据阅读材料用配方法解决下列问题：

(1)、分解因式： $x^{2} - 4 x - 5$ ；

(2)、求 $a^{2} + 2 a + 2021$ 的最小值；

(3)、求 $- x^{2} + 2 x + 2019$ 的最大值.

查看试题解析
26. 已知直线 $l_{1} / / l_{2}$ ，点A，C分别在 $l_{1}$ ， $l_{2}$ 上，点B在直线 $l_{1}$ ， $l_{2}$ 之间，且 $∠ B C N < ∠ B A M \leq 90 °$ .

(1)、如图①，求证： $∠ A B C = ∠ B A M + ∠ B C N$ .
阅读并将下列推理过程补齐完整：

过点B作 $B G / / N C$ ，因为 $l_{1} / / l_{2}$ ，

所以 $A M / /$ （）

所以 $∠ A B G = ∠ B A M$ ， $∠ C B G = ∠ B C N$ （）

所以 $∠ A B C = ∠ A B G + ∠ C B G = ∠ B A M + ∠ B C N$ .

(2)、如图②，点D，E在直线 $l_{1}$ 上，且 $∠ D B C = ∠ B A M$ ，BE平分 $∠ A B C$ .
求证： $∠ D E B = ∠ D B E$ ；

(3)、在（2）的条件下，如果 $∠ C B E$ 的平分线BF与直线 $l_{1}$ 平行，试确定 $∠ B A M$ 与 $∠ B C N$ 之间的数量关系，并说明理由.

查看试题解析