四川省遂宁市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-09-03 类型:期末考试
一、单选题
-
1. 下列各式: , , ,5, , , ,分式有( )A、1个 B、2个 C、3个 D、4个2. 下列从左到右变形正确的是( )A、 = B、 = C、 =x﹣y D、 =3. 若分式 的值为 ,则 的值为( )A、 B、 C、3或-3 D、4. 若a=(﹣ )-2 , b=(﹣ )0 , c=0.75﹣1 , 则( )A、a>b>c B、c>a>b C、c>b>a D、a>c>b5. 据医学研究:新型冠状病毒的平均直径约为100纳米.其中1纳米=1.0×10﹣9米,则新型冠状病毒的平均直径用科学记数法表示为( )A、1.0×10﹣9米 B、1.0×10﹣8米 C、1.0×10﹣7 D、1.0×10﹣6米6. 在函数 中,自变量 的取值范围是( )A、 B、 C、 且 D、7. 如图,若棋子“炮”的坐标为 ,棋子“马”的坐标为 ,则棋子“车”的坐标为( )
 A、 B、 C、 D、8. 若关于 的分式方程 有增根,则 的值为( )A、 B、 C、 D、9. 等腰三角形周长为20cm,底边长ycm与腰长xcm之间的函数关系是 )A、 B、 C、 D、10. 一次函数 的图象如图所示,则下列选项中错误的说法是( )
A、 B、 C、 D、8. 若关于 的分式方程 有增根,则 的值为( )A、 B、 C、 D、9. 等腰三角形周长为20cm,底边长ycm与腰长xcm之间的函数关系是 )A、 B、 C、 D、10. 一次函数 的图象如图所示,则下列选项中错误的说法是( )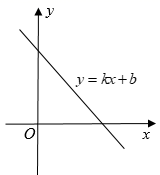 A、 B、当 时, C、若点 与 都在直线 上,则 D、将函数图象向左平移1个单位后,图象恰好经过坐标原点,则11. 为响应“科技扶贫”,我区某单位向一贫困村赠送1080本农村实用书籍,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱多用6个;已知每个B型包装箱比每个A型包装箱可少装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )A、 B、 C、 D、12. 如图,点P是菱形ABCD边上的动点,它从点A出发沿A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
A、 B、当 时, C、若点 与 都在直线 上,则 D、将函数图象向左平移1个单位后,图象恰好经过坐标原点,则11. 为响应“科技扶贫”,我区某单位向一贫困村赠送1080本农村实用书籍,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱多用6个;已知每个B型包装箱比每个A型包装箱可少装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )A、 B、 C、 D、12. 如图,点P是菱形ABCD边上的动点,它从点A出发沿A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( ) A、
A、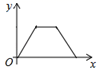 B、
B、 C、
C、 D、
D、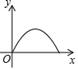 13. 某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成下表:
13. 某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成下表:投中次数
2
3
5
6
7
8
人数
1
2
3
2
1
1
则关于这10名队员投中次数组成的数据,下列说法错误的是( )
A、平均数为5 B、中位数为5 C、众数为5 D、方差为514. 下列命题是真命题的是( ).A、对角线相互垂直的四边形是平行四边形 B、对角线相等且相互垂直的四边形是菱形 C、四条边相等的四边形是正方形 D、对角线相等且相互平分的四边形是矩形15. 如图,点P是Rt△ABC中斜边AC (不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( )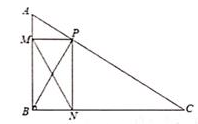 A、1.5 B、2 C、4.8 D、2.416. 如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形 ,若测得 之间的距离为 ,点 之间的距离为 ,则线段 的长为( )
A、1.5 B、2 C、4.8 D、2.416. 如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形 ,若测得 之间的距离为 ,点 之间的距离为 ,则线段 的长为( )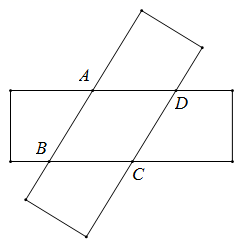 A、 B、 C、 D、17. 如图,小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中任选两个作为补充条件,使▱ABCD为正方形.现有下列四种选法,你认为其中错误的是( )
A、 B、 C、 D、17. 如图,小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中任选两个作为补充条件,使▱ABCD为正方形.现有下列四种选法,你认为其中错误的是( ) A、②③ B、①③ C、①② D、③④18. 如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )
A、②③ B、①③ C、①② D、③④18. 如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )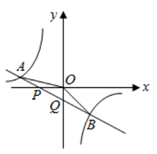 A、①③ B、②③④ C、①③④ D、②④
A、①③ B、②③④ C、①③④ D、②④二、填空题
-
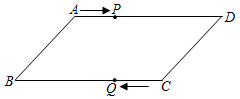
19. 化简 的结果是.20. 函数 中x的取值范围是.21. 若关于x的方程 无解,则m=.22. 某校有31名同学参加某比赛,预赛成绩各不同,要取前16名参加决赛,小红已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这31名同学成绩的.23. 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止).在运动以后,当t=时以P、D、Q、B四点组成的四边形为平行四边形.
 24. 如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:①在点M的运动过程中,四边形CEMD可能成为菱形;②连接HM,无论点M运动到何处,都有DM= HM;③点M位置变化,连接HD,使得∠DHC=60°时,2BE=DM;④无论点M运动到何处,∠CHM一定大于135°;以上结论正确的有(把所有正确结论的序号都填上).
24. 如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:①在点M的运动过程中,四边形CEMD可能成为菱形;②连接HM,无论点M运动到何处,都有DM= HM;③点M位置变化,连接HD,使得∠DHC=60°时,2BE=DM;④无论点M运动到何处,∠CHM一定大于135°;以上结论正确的有(把所有正确结论的序号都填上).
三、解答题
-
25. 计算:(1)、|﹣2|﹣ +(﹣1)2021;(2)、( ﹣2)÷ .26. 先化简,再求值: ,其中a是4的平方根.27. 关于x的方程: - =1.(1)、当a=3时,求这个方程的解;(2)、若这个方程有增根,求a的值.28. 如图,在 中, 是 边上的中线,点E是 的中点,过点A作 交 的延长线于F,连接 .
 (1)、求证: ;(2)、若 ,求证:四边形 是菱形.29. 骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的 型车去年6月份销售总额为3.2万元,今年经过改造升级后 型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的 型车数量相同,则今年6月份 型车销售总额将比去年6月份销售总额增加 .
(1)、求证: ;(2)、若 ,求证:四边形 是菱形.29. 骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的 型车去年6月份销售总额为3.2万元,今年经过改造升级后 型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的 型车数量相同,则今年6月份 型车销售总额将比去年6月份销售总额增加 ., 两种型号车的进货和销售价格表:
型车
型车
进货价格(元 辆)
1100
1400
销售价格(元 辆)
今年的销售价格
2400
(1)、求今年6月份 型车每辆销售价多少元;(2)、该车行计划7月份新进一批 型车和 型车共50辆,且 型车的进货数量不超过 型车数量的两倍,应如何进货才能使这批车获利最多?30. 某中学举办“信息技术知识答题竞赛”,八、九年级根据初赛成绩各选出5名选手组成代表队参加学校决赛,现将两个队各选出的5名选手的决赛成绩绘制成如下统计图表.八,九年级决赛成绩的条形统计图

平均分(分)
中位数(分)
众数(分)
方差(分 )
八年级
85
85
70
九年级
80
(1)、根据图表信息填空: , , ;(2)、计算九年级代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.31. 已知一次函数y=kx+b与反比例函数 的图象交于A(﹣3,2)、B(1,n)两点.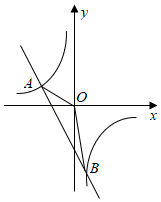 (1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、直接写出不等式 的解集.(4)、点P在x轴上,当△PAO为等腰三角形时,直接写出点P的坐标.32. 在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG
(1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、直接写出不等式 的解集.(4)、点P在x轴上,当△PAO为等腰三角形时,直接写出点P的坐标.32. 在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG (1)、将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.(2)、将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系.请写出你的猜想,并加以证明.
(1)、将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.(2)、将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系.请写出你的猜想,并加以证明.