四川省南充市2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-09-03 类型：期末考试

进入出卷网下载

一、单选题

1. 要使式子﹣ $\sqrt{x - 3}$ 有意义，则x的值可以为（）

A、﹣6 B、0 C、2 D、π

查看试题解析
2. 在数据4，5，6，5中添加一个数据，而平均数不发生变化，则添加的数据为（）

A、0 B、5 C、4.5 D、5.5

查看试题解析
3. 对于一次函数y＝﹣2x＋3，下列说法不正确的是（）

A、图象经过点（﹣1，5） B、图象与x轴交于点（1.5，0） C、图象不经过第三象限 D、当x＞2时，y＞﹣1

查看试题解析
4. 如图，DE是△ABC的中位线，直角∠AFB的顶点在DE上，AB＝5，BC＝8，则EF的长为（）

A、1 B、1.5 C、2 D、不能确定

查看试题解析
5. 如图，四边形ABCD中，∠B＝∠D＝90°，AB＝3 $\sqrt{2}$ ，BC＝4 $\sqrt{2}$ ，AD＝CD，则AD•CD（）

A、12 $\sqrt{2}$ B、24 C、12 $\sqrt{3}$ D、25

查看试题解析
6. 计算 $\sqrt{45}$ ÷3 $\sqrt{2}$ × $\sqrt{\frac{2}{5}}$ 的结果正确的是（）

A、1 B、2.5 C、5 D、6

查看试题解析
7. 如图，正方形ABCD中，点O在△ACD内，∠OAC＝∠ODA，则∠AOD＝（）

A、120° B、125° C、130° D、135°

查看试题解析
8. 两组数据：3，a，b，5与a，4，2b的平均数都是3，若将这两组数据合并为一组新数据，下列说法错误的是（）

A、平均数仍是3 B、众数是3 C、中位数是3 D、方差是1

查看试题解析
9. 如图，将矩形ABCD沿AE折叠，使点B落在边CD上点F处，若AD＝8cm，CE＝3cm，则边AB的长为（）

A、9cm B、10cm C、12cm D、13cm

查看试题解析
10. 已知：如图1，点G是BC的中点，点H在AF上，动点P以每秒2cm的速度沿图1的边线运动，运动路径为：G→C→D→E→F→H，相应的△ABP的面积y（cm²）关于运动时间t（s）的函数图象如图2，若AB=6cm，则下列四个结论中正确的个数有（）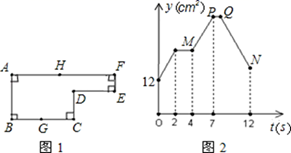

①图1中的BC长是8cm， ②图2中的M点表示第4秒时y的值为24cm² ，

③图1中的CD长是4cm， ④图2中的N点表示第12秒时y的值为18cm².

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算（ $\sqrt{2}$ ＋1）（ $\sqrt{2}$ ﹣1）² ，结果是.

查看试题解析
12. 一组勾股数，若其中两个为15，8，则第三个数为.

查看试题解析
13. 一家手表厂对一批手表抽查了10块，日走时误差数据如表（单位：s）.这10块手表日走时误差的平均数和中位数之和为.

日误差

0

1

2

3

块数

3

4

2

1

查看试题解析
14. 如图，点P（﹣4，3）在一次函数y＝kx＋b（k≠0）的图象上，则关于x的不等式kx＋b＜3的解集是.

查看试题解析
15. 如图，在直角坐标系中，矩形OABC的两邻边在坐标轴上，顶点B（6，4），经过边BC上一点P（4，m）的直线将矩形面积平分，则这条直线的解析式为.

查看试题解析
16. 如图，▱ABCD中，AC，BD交于O，AE平分∠BAD，EC＝CD＝1，∠ECD＝2∠CDA.下列结论：①AC平分∠EAD；②OE＝ $\frac{1}{4}$ AD；③BD＝ $\sqrt{7}$ ；④S▱ABCD＝ $\sqrt{3}$ .正确的有个.

查看试题解析

三、解答题

17. 确定3 $\sqrt{48}$ ﹣2 $\sqrt{12}$ ＋6 $\sqrt{\frac{1}{3}}$ 在哪两个整数之间.

查看试题解析
18. 如图，E，F分别在正方形ABCD的两边上，BE＝CE＝2，AF＝5，求∠AEF的度数.

查看试题解析
19. 如图，是甲、乙两名射击运动员一次训练中10次射击环数折线统计图.选出方差小的计算方差.

查看试题解析
20. 在直角坐标系中，说明三点A（﹣3， $\frac{1}{2}$ ），B（4，4），C（6，5）在同一直线上.

查看试题解析
21. 在一次中学生田径运动会上，根据参加男子跳高运动员的初赛成绩（单位：m），绘制出如下两幅统计图（未完善）.请根据相关信息，解答下列问题：

(1)、扇形统计图中a＝，初赛成绩为1.70m对应扇形的圆心角为；

(2)、这组初赛成绩的众数是m，中位数是m；

(3)、根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员小王能否进入复赛？为什么？

查看试题解析
22. 如图，四边形ABCD中，E为边BC的中点，BD与AE交于O，BO＝DO，AO＝2EO.AC与BD交于F.

(1)、求证：F是AC的中点.

(2)、求S_△ACD：S_△ABD的值.

查看试题解析
23. 如图，直线l₁：y＝﹣x﹣3与过点A（0，3）的直线l₂交于点C（m，1），与y轴交于点B.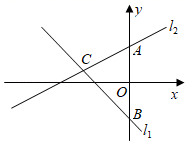

(1)、求直线l₂的解析式；

(2)、点P在直线l₁上，PQ∥x轴，交直线l₂于点Q，若PQ＝AB，求点P的坐标.

查看试题解析
24. 如图，平行四边形ABCD中，AE⊥CD于E，BF平分∠ABC与AD交于F.AE与BF交于G.

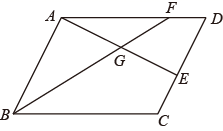(1)、延长DC到H，使CH＝DE，连接BH.求证：四边形ABHE是矩形.

(2)、在（1）所画图形中，在CH的延长线上取HK＝AG，当AE＝AF时，求证：CK＝AD.

查看试题解析
25. 如图，直线y＝﹣ $\frac{12}{5}$ x＋12与x轴交于A，与y轴交于B.直线BC与AB关于y轴对称.将BC向左平移经过点D（﹣13，12），与x轴交于E.F在DB的延长线上，G在第四象限直线AB上，EF与DG交于P.

(1)、求直线DE的解析式.

(2)、判断四边形BDEC的形状，并证明你的结论.

(3)、当动点F，G满足AG＝BF时，求证：EF＝DG.

(4)、在（3）的动态条件下，△PDE能否成为等边三角形.（不用证明）

查看试题解析

日误差	0	1	2	3
块数	3	4	2	1