四川省广元市青川县2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-09-03 类型:期末考试
一、单选题
-
1. 下列式子中属于最简二次根式的是( )A、 B、 C、 D、2. 函数 中自变量x的取值范围是( )A、x≤2 B、x=3 C、x<2且x≠3 D、x≤2且x≠33. 如果一直角三角形的两边长分别为3和5,则第三边长是( )A、4 B、 C、4或 D、以上答案都不正确4. 实数 在数轴上的对应点的位置如图所示,下列结论正确的是( )
 A、 B、 C、 D、5. 下列命题中错误的是( )A、两组对角分别相等的四边形是平行四边形 B、矩形的对角线相等 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分且相等的四边形是正方形6. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A、 B、 C、 D、5. 下列命题中错误的是( )A、两组对角分别相等的四边形是平行四边形 B、矩形的对角线相等 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分且相等的四边形是正方形6. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( ) A、 B、 C、 D、7. 若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )A、平均数为10,方差为2 B、平均数为11,方差为3 C、平均数为11,方差为2 D、平均数为12,方差为48. 已知kb<0,且k>0,则函数y=kx+b的图象大致是( )A、
A、 B、 C、 D、7. 若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )A、平均数为10,方差为2 B、平均数为11,方差为3 C、平均数为11,方差为2 D、平均数为12,方差为48. 已知kb<0,且k>0,则函数y=kx+b的图象大致是( )A、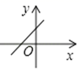 B、
B、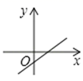 C、
C、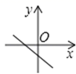 D、
D、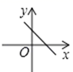 9. 如图,在菱形ABCD中,点E,F、G,H分别是边,AB,BC,CD和DA的中点,连接EF.FG.GH和HE.若EH=3EF,则下列结论正确的是( )
9. 如图,在菱形ABCD中,点E,F、G,H分别是边,AB,BC,CD和DA的中点,连接EF.FG.GH和HE.若EH=3EF,则下列结论正确的是( )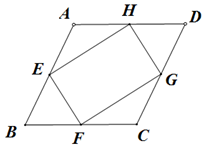 A、AB= EF B、AB=2 EF C、AB=3EF D、AB= EF10. 如图,正方形ABCD中,E、F均为中点,则下列结论中:①AF⊥DE; ②AD=BP; ③PE+PF= PC; ④PE+PF=PC.其中正确的是( )
A、AB= EF B、AB=2 EF C、AB=3EF D、AB= EF10. 如图,正方形ABCD中,E、F均为中点,则下列结论中:①AF⊥DE; ②AD=BP; ③PE+PF= PC; ④PE+PF=PC.其中正确的是( ) A、①④ B、①②④ C、①③ D、①②③
A、①④ B、①②④ C、①③ D、①②③二、填空题
-
11. 若 有意义,则 的取值范围是.12. 把命题“如果直角三角形的两直角边长分别为a、b,斜边长为c,那么 ”的逆命题改写成“如果……,那么……”的形式:.13. 一根弹簧的原长为12 cm,它能挂的重量不能超过15 kg并且每挂重1kg就伸长 cm,写出挂重后的弹簧长度y(cm)与挂重 x(kg)之间的函数关系式并标明 x 的取值范围.14. 某校举行“纪念香港回归21周年”演讲比赛,共有15名同学进入决赛(决赛成绩互不相同),比赛将评出金奖1名,银奖3名,铜奖4名.某参赛选手知道自己的分数后,要判断自己能否获奖,他应当关注的是有关成绩的 . (填“平均数”“中位数”或“众数”)15. 如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为.
 16. 如图,在矩形 中,E是边 上一点,将矩形沿 折叠,点D的对应点F恰好落在边 上, 交 于点H,连接 .若 ,则 度.
16. 如图,在矩形 中,E是边 上一点,将矩形沿 折叠,点D的对应点F恰好落在边 上, 交 于点H,连接 .若 ,则 度.
三、解答题
-
17. 计算:(1)、(2)、 .18. 先化简,再求值: ,其中x= ,y= .19. 某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
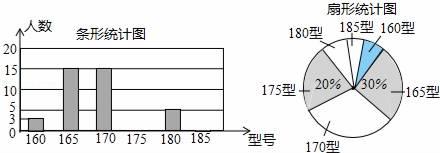
根据以上信息,解答下列问题:
(1)、该班共有多少名学生?其中穿175型校服的学生有多少?(2)、在条形统计图中,请把空缺部分补充完整.(3)、在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;(4)、求该班学生所穿校服型号的众数和中位数.20. 为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路 的一侧点 处有一村庄,村庄 到公路 的距离为800米,假使宣讲车 周围1000米以内能听到广播宣传,宣讲车 在公路 上沿 方向行驶时: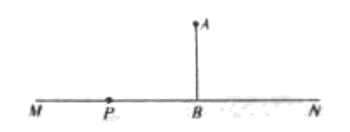 (1)、请问村庄能否听到宣传,并说明理由;(2)、如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?21. 已知直线y=kx+b(k≠0)经过点A(3,0),B(1,2)(1)、求直线y=kx+b的函数表达式;(2)、若直线y=x﹣2与直线y=kx+b相交于点C , 求点C的坐标;(3)、写出不等式kx+b>x﹣2的解.22. 观察、思考与验证
(1)、请问村庄能否听到宣传,并说明理由;(2)、如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?21. 已知直线y=kx+b(k≠0)经过点A(3,0),B(1,2)(1)、求直线y=kx+b的函数表达式;(2)、若直线y=x﹣2与直线y=kx+b相交于点C , 求点C的坐标;(3)、写出不等式kx+b>x﹣2的解.22. 观察、思考与验证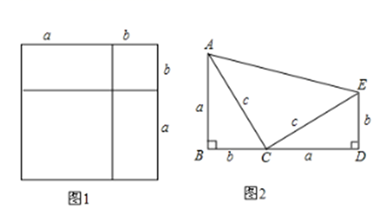 (1)、如图1是一个重要公式的几何解释,请你写出这个公式 .(2)、如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°.(3)、伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的<新英格兰教育日志》上),请你写出验证过程.23. 某工程队要招聘甲、乙两种工种的工人共160人,甲、乙两种工人的月工资分别为甲800元和乙1200元.现要求乙工种的人数不少于甲工种人数的3倍.(1)、设招聘甲工种x人,工程队每月应付甲、乙两工种的工人工资共为y元,求y与x的函数关系式.(2)、当x为何值时,y有最小值,并求最小值.24. 如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)、如图1是一个重要公式的几何解释,请你写出这个公式 .(2)、如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°.(3)、伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的<新英格兰教育日志》上),请你写出验证过程.23. 某工程队要招聘甲、乙两种工种的工人共160人,甲、乙两种工人的月工资分别为甲800元和乙1200元.现要求乙工种的人数不少于甲工种人数的3倍.(1)、设招聘甲工种x人,工程队每月应付甲、乙两工种的工人工资共为y元,求y与x的函数关系式.(2)、当x为何值时,y有最小值,并求最小值.24. 如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.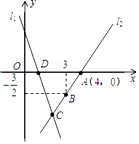 (1)、求直线l2的解析表达式;(2)、求△ADC的面积;(3)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请求出点P的坐标.25. 如图,在▱ABCD中,AF是∠BAD的平分线,交BC于点F,与DC的延长线交于点N.CE是∠BCD的平分线,交AD于点E,与BA的延长线交于点M.
(1)、求直线l2的解析表达式;(2)、求△ADC的面积;(3)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请求出点P的坐标.25. 如图,在▱ABCD中,AF是∠BAD的平分线,交BC于点F,与DC的延长线交于点N.CE是∠BCD的平分线,交AD于点E,与BA的延长线交于点M. (1)、试判断四边形AFCE的形状,并说明理由;(2)、若BE⊥ME,证明四边形ABFE是菱形.26. 如图,在 中, , , ,点 从点 出发沿 方向以4cm/s的是速度向点 匀速运动,同时点 从 出发沿 方向以2cm/s的速度向点 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点 、 运动的时间是 s.过点 作 于点 ,连接 、 .
(1)、试判断四边形AFCE的形状,并说明理由;(2)、若BE⊥ME,证明四边形ABFE是菱形.26. 如图,在 中, , , ,点 从点 出发沿 方向以4cm/s的是速度向点 匀速运动,同时点 从 出发沿 方向以2cm/s的速度向点 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点 、 运动的时间是 s.过点 作 于点 ,连接 、 . (1)、求证: ;(2)、四边形 能够成为菱形吗?如果能,求出相应的 值;如果不能,请说明理由;(3)、当 为何值时, 为直角三角形?请说明理由.
(1)、求证: ;(2)、四边形 能够成为菱形吗?如果能,求出相应的 值;如果不能,请说明理由;(3)、当 为何值时, 为直角三角形?请说明理由.